13.6: Coordination Complexes
- Page ID
- 140105
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The bond that forms between a Lewis base and a Lewis acid is sometimes called a dative bond or a coordinate bond. The term used for the donation of a Lewis base to a Lewis acid, without any other bonding changes, is coordination. Another term for Lewis acid-base complexes, especially used in the context of transition metal chemistry, is coordination complexes. Sometimes the Lewis base is referred to as a ligand; more generally, a ligand is just one molecule that binds to another.

Figure AB6.1. Formation of a Lewis acid-base complex.
An example of a coordination complex is hexaaquo cobalt dichloride, Co(H2O)6Cl2. This compound contains a Co2+ ion. This electrophilic metal ion is coordinated by six nucleophilic water ligands. Because the water molecules are neutral, the complex still has a 2+ charge overall. There are two chloride counterions to balance the charge, but the chlorides are not attached to the complex ion.
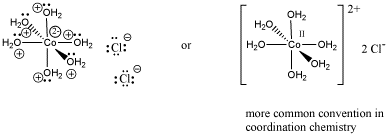
Figure AB6.2. Representations of a transition metal coordination complex.
Notice that the usual Lewis conventions are usually abandoned in drawing coordination complexes of transition metals. With so many different nucleophiles sticking to the Lewis acid, the number of formal charges that must be drawn becomes very cumbersome. Usually the oxidation state of the metal cation is denoted. The oxidation state essentially means the charge on the metal cation and it is written in Roman numerals beside the metal atom. In addition, the overall charge on the Lewis acid-base complex is given, with square brackets indicating that the charge belongs to the entire complex within the brackets. Exactly where that charge resides is up to the reader to consider.
Coordination complexes are frequently useful in mining and metallurgy. For example, nickel can be extracted from nickel ore by converting the nickel into Ni(CO)4 via addition of carbon monoxide. Ni(CO)4, or tetracarbonyl nickel, is a gas that can be easily separated from the solid ore. When removed from the presence of carbon monoxide, the coordination complex decomposes back into Ni and CO.
4-1.gif?revision=1)
Figure AB6.3. Tetracarbonyl nickel.
Problem AB6.1.
These questions concern the formation of tetracarbonyl nickel.
a) Based on what you know about transition metals, is the nickel most likely a Lewis acid or a Lewis base?
b) Draw the Lewis structure for carbon monoxide, CO. Make sure each atom has an octet. Make sure you add formal charges.
c) Based on formal charge considerations, which atom in carbon monoxide will bind to the nickel?
d) Using arrow notation, show the coordination of CO to Ni. Do this one step at a time, showng each CO molecule binding to the nickel and the new complex that results after each step.
e) Why does nickel bind four carbon monoxide ligands, and not three or five?
Another example is seen in the liquid extraction of metals from ores. Often, a metal is coordinated by some kind of ligand that changes the solubility of the metal atom, so that it can be extracted from the ore with a solvent. The solvent is usually water, but other liquids could be used. One of the easiest cases to picture on paper is the leaching of gold from gold ores with cyanide.
Often, coordination of a ligand to a metal changes many properties of the metal, in addition to changing its solubility. Transition metals have different oxidation states, meaning they can give up different numbers of electrons and become cations with different charges. Sometimes, this event happens more easily upon coordination. In the case of gold, the gold atom can react with air and become a gold cation in the presence of cyanide.
Cyanide is an anion, so it would be added as a salt, such as sodium cyanide, NaCN, or potassium cyanide, KCN. The resulting complex, Au(CN)2, is actually a complex anion, and it would be associated with one of the counterions added, such as KAu(CN)2. It is not completely clear why the gold binds two cyanides, but binding two ligands is common in the chemistry of gold and silver, and is based on molecular orbital considerations that are beyond the level of this course.
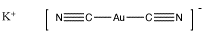
Figure AB6.4. Gold dicyanide complex ion, shown here with a potassium counterion.
This complex salt is water-soluble, so it can be removed from the ore with water. Later, it must be converted back into pure gold via electrochemical reactions. These reactions are not related to acid-base chemistry and will not be covered in this course.
Problem AB6.2
These questions concern the formation of the potassium dicyano gold complex.
a) Based on what you know about transition metals, is the gold most likely a Lewis acid or a Lewis base?
b) Draw the Lewis structure for cyanide, CN-. Make sure each atom has an octet. Make sure you add formal charges.
c) Based on formal charge considerations, which atom in cyanide will bind to the gold?
d) Using arrow notation, show the coordination of cyanide to Au+. (We will simplify and assume the gold has already been oxidized). Do this one step at a time, showing each cyanide molecule binding to the gold ion and the new complex that results after each step.
Perhaps some of the most interesting coordination complexes involve transition metals in biology. The most familiar of these compounds is haemoglobin. Haemoglobin is a complex protein that contains a crucial iron atom. The iron is present as a 2+ cation, but the haeme ring that binds to the iron has a 2- charge, so overall there is no charge on the complex. The iron is still electrophilic, however, and it can bind an oxygen molecule. Much more oxygen can be carried in the bloodstream this way than if the oxygen simply dissolved in the blood.
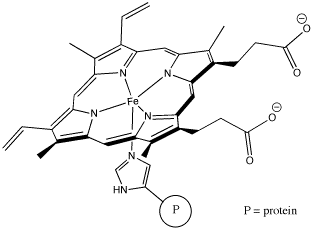
Figure AB6.4. Hemoglobin. Most of the molecule is not shown. The iron-containing heme subunit is attached to a large protein via an imidazole ring in a histidine amino acid residue.
Problem AB6.3.
These questions concern the formation of the oxyhaemoglobin.
a) Based on what you know about transition metals, is the iron most likely a Lewis acid or a Lewis base?
b) Draw the Lewis structure for oxygen molecule, O2. Make sure each atom has an octet. Make sure you se if there are any formal charges.
N.B. This Lewis structure may not agree completely with the molecular orbital view of the molecule, but it is all we have to work with for our current method of understanding coordination.
c) Using arrow notation, show the coordination of oxygen to Fe2+.
d) There has been a great deal of research into the exact geometry of the dioxygen complex. Based on your Lewis structure of oxygen, show how you think the oxygen is attached to the iron. How would you describe the geometry?
There is another interesting event that happens when oxygen binds to the iron in haemoglobin. After binding O2, the iron actually transfers a single electron to the oxygen, becoming a Fe3+ cation. Although deoxyhaemoglobin, the Fe2+ or Fe(II) species, is purple, many Fe3+ or Fe(III) compounds are red. Thus, oxyhaemoglobin is red.
It is also interesting to note that we are used to seeing iron-containing materials turn a sort of red-brown colour when they have been exposed to oxygen for a long time, especially in the presence of water and salts. Our cars, trains and bridges eventually rust as the iron in their steel turns to reddish iron oxide. William Tolman, a researcher in bioinorganic chemistry at the University of Minnesota, likes to raise the following question: we rely on iron complexes to carry oxygen through our salt-water bloodstream, so why don't we get rusty?
The answer is that, in a sense, we do. It has been estimated that after several passes through our bloodstream, a haemoglobin molecule meets its end when the oxygen fails to detach and the iron complex decomposes to an iron oxide. That's one reason why you need to eat a diet that contains iron, to replenish your iron stores in order to make new haemoglobin on a regular basis.
To see some additional problems that will help you get to know coordination compounds, go to the main coordination compound chapter. In particular, it is really useful to be able to count electrons in coordination chemistry. Counting electrons is just like learning Lewis structures, except that instead of going to a maximum count of eight electrons, we can go to a maximum of eighteen electrons. That's because the noble gas configuration for a transition metal would have eighteen electrons, not eight. To learn how to count electrons in coordination complexes, go here.

