Redox Reactions

Learning Objectives – Oxidation and Reduction Reactions

After completing this unit the student will be able to:

1. Define electrochemical process.
2. Differentiate between oxidation and reduction using a simple equation or daily products.
3. Determine oxidation numbers and balance redox equations.
4. Show relationship between electric current from redox reaction to the rate of reaction.
5. Show relationship between voltage and free energy change of the reaction.
6. Describe the relationship between work and potential difference of a reaction.
7. Show how free energy is related to electrochemical reaction.
8. Show relationship between current, voltage and resistance.
9. Differentiate between Galvanic and Electrolytic cells.
10. Calculate the voltage and Gibbs free energy for a chemical reaction.
11. Assemble a redox reaction using two half equations.
12. Determine the spontaneity of a chemical reaction.
13. Write free hand notation of a redox reaction.
14. Use the Nernst equation in solving redox reactions.
15. Illustrate redox reaction using market examples of dry-cell batteries, lead-acid storage batteries, a fuel-cell car, Hydrogen–oxygen fuel cell etc.
16. Solve any redox reaction problems using the electromotive force values in a standard reduction potentials.

Background Material

Please read Chapter 10 on Redox Reaction on Page 230 in the textbook “Analytical Chemistry and Quantitative Analysis” by David S. Hage and James D. Carr.

Questions before class

1. What is electrochemical process? Define oxidation and reduction using electrons.

   Solution:

 

2. Using the following equation, 2Mg (s) + O₂ (g) → 2MgO (s); write two half equations for oxidation and reduction.

   Solution:

 

3. Make a summary of rules governing oxidation numbers and balancing equations using oxidation numbers.

   Solution:

 



 

4. Make a summary of rules governing redox reactions and how they are balanced in basics and acidic media.

 

5. Write an equation relating electric charge (q) with measured coulombs (C).

   Solution:

 


 

6. Give an equation for current relating it to quantity of charge (q) and time (t).

   Solution:

 


 

7. Write a relationship equation between work (w) resulting from charge (q) moving through a potential difference (E):

   Solution:

 

8. Relate free energy change (ΔG) and maximum possible electrical work.

   Solution:

 

9. Using Ohm’s law give the relationship between current (I) and potential (V) or resistance (Ω)

   Solution:

 

10. What is the relationship between Power and work?

    Solution:

 

11. Using an example define a Galvanic cell, draw a sketch of the cell, name the electrodes, anode, cathode, salt bridge, write down the half reactions and a balanced overall cell equation.

    Solution:

 

12. Write the cell reaction-using notation.

    \[\ce{Cd}(s) \mid \ce{Cd(NO3)2}(aq) \mid\mid \ce{AgNO3}(aq) \mid \ce{Ag}(s)\nonumber\]

    Solution:

 

13. Draw a sketch representing the standard hydrogen half equation at 1-atm and 1M acidic solution.

    Solution:

 

14. How can you use standard electrode potentials to calculate the cell potential, illustrate using SHE and a silver half cell (Ag⁺(aq)+e^-↔Ag(s)    E° = 0.799)

    

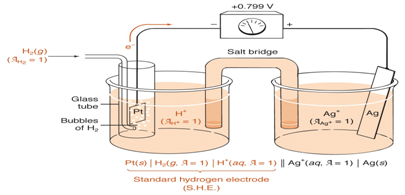
15. Write down and equation for calculating the overall electrode potential of the cell.

    Solution:

 


 

16. Write down Nernst equation.

    Solution:

 

17. Use Nernst equation calculate the overall cell potential for the following reaction:

    \[\ce{Ag} (s) \mid \ce{Ag+} (aq)\: \mathrm{(0.001 = a)} \mid\mid \ce{Ag+} (aq)\: \mathrm{(0.010 = a)} \mid \ce{Ag} (s)\nonumber\]

    Solution:

 

18. What is the relationship between ΔG, ΔH, T and ΔS?

    Solution:

 

 

Questions in class Group 1:

Given a cell with the following half equations:

\[\ce{C} (s) + \ce{2O^2-} (aq) → \ce{CO2} (g) + \ce{4e-}\nonumber\]

\[\ce{Ga^3+} (aq) + \ce{3e-} → \ce{Ga} (s)\nonumber\]

This cell was 100% efficient and produces 17.26 kilogram of gallium metal in exactly 1260 minutes.

1. Write a balanced equation for the reaction;

   Solution:

 

 

 

2. Calculate the quantity of gallium formed in moles;

   Solution:

             

 

 

 

3. Calculate the number of electron moles passed through the cell in forming gallium metal?

   Solution:

           

 

 

 

 

4. Calculate the charge (C) carried by the electrons that passed through the cell;

   Solution:

           

 

 

5. Calculate the currents (A) using the charge (C) passed through the cell in a period of 1260 minutes.

   Solution:

 

 

           

 

 

Questions in class Group 2:

Given the cell: Cu(s) | Cu²⁺ (0.50 M) || I^- (0.30 M) | I₃^- (0.15 M) | Pt; and information below,     

\[\ce{I3- + 2e- → 3I-} \hspace{30px} E^0 = \mathrm{0.535\: V}\nonumber\]

\[\ce{Cu^2+} + \ce{2e-} → \ce{Cu}(s) \hspace{30px} E^0 = \mathrm{0.339\: V}\nonumber\]

1. What does | stands for in the notation?

   Solution:

 

2. What does || stands for in the notation?

   Solution:

 

3. Write the ionic half-cell reactions for the cathode and anode.

   Solution:

 

4. Write the overall ionic cell equation for the reaction and its E⁰ value.

   Solution:

 

5. Calculate the voltage of the cell at 298K.

   Solution:

 

 

Questions in class Group 3:

As researchers look for alternative fuels, the production of H₂ is being extensively studied. The following example shows a reduction reaction that can be used to produce H₂ under basic conditions:

\[\ce{2H2O} (l) + \ce{2e-} → \ce{H2} (g) + \ce{2OH-} (aq) \hspace{30px} E^o = \mathrm{- 0.83\: V}\nonumber\]

1. What is the Nernst expression for this half-cell?

   Solution:

 

 

 

2. Write the Nernst expression so that the influence of the [OH^-] appears as a function of pH assuming that activity of H₂ = 4.0 x 10^-5.

   Solution:

 

 

 

 

 

3. What is the value of E for this reaction when the pH of the solution is maintained at 7.00?

   Solution:

 

 

 

 

4. What is the value of E for this reaction when the pH of the solution is maintained at 10.00?

   Solution:

 

 

 

 

Questions in class Group 4:

Use the following cell between Cu/Zn and the electrode potentials for the half cells to answer the question:

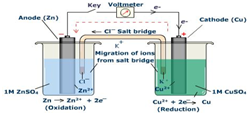
\[\ce{Zn^2+}(aq) + \ce{2e-} → \ce{Zn}(s)\: \textrm{------------------------} \: E^o = \mathrm{-0.76\:V}\nonumber\]

\[\ce{Cu^2+}(aq) + \ce{2e-} → \ce{Cu}(s)\: \textrm{------------------------} \: E^o = \mathrm{0.34\:V}\nonumber\]

1. What is the overall cell equation for the reaction?

   Solution:

 

 

 

2. What is the overall cell potential for the reaction?

   Solution:

 

3. Calculate the Gibbs free energy (ΔG) for the reaction in kilojoules?

   Solution:

 

4. What is the equilibrium constant for the reaction?

   Solution:

 

5. What is the role of the salt bridge?

   Solution:

 

 

Questions in class Group 5:

Using standard reduction potentials, calculate the potential for the following cell at 298 K:

\[\mathrm{Zn \mid Zn^{2+}(\textit{aq}),\: 0.1\: M \mid\mid Cu^{2+}(\textit{aq}),\: 1.0\: M \mid Cu}\nonumber\]

1. Why is it not possible to generate electrical current by simply placing strips of copper and zinc in a beaker containing an aqueous solution of Zn(NO₃)₂ and Cu(NO₃)₂?

   Solution:

 

2. Using shorthand notation, Zn | Zn²⁺(aq), 0.1 M || Cu²⁺(aq), 1.0 M | Cu, write the half equation for anode, cathode and the overall reaction equation:

   Solution:

 

 

 

3. What is the expression for Q and calculate the Q value?

   Solution:

 

4. Calculate the E^o value for the reaction?

   Solution:

 

5. What is the overall potential of the cell?

   Solution:

 

6. Is the reaction spontaneous or not?

   Solution:

 

Contributors and Attributions

• Grant Wangila, University of Arkansas Pine Bluff ([e-mail])
• Sourced from the Analytical Sciences Digital Library