Problem 1
- Page ID
- 302961
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. Calculate the concentration of free calcium(II) ions in a solution prepared with initial concentrations of calcium of 0.020 M and EDTA4– of 0.10 M.
This is our first example involving a water-soluble metal complex. The general form of these equations is that a metal ion (M) reacts with a ligand (L) to form a water-soluble complex.
\[\mathrm{M(aq) + L(aq) \leftrightarrow ML(aq) \hspace{60px} K_f}\nonumber\]
Usually we appreciate that these are all water-soluble species and omit the (aq) notation from the equations. The general form of the equation is referred to as a formation constant, hence the notation Kf for the equilibrium constant. If you examine the values of Kf in the table, you will see that many of these are reasonably large values. In fact, because they are large, it is common for tables to report the logKf value rather than the Kf value. It makes sense that many of these in the table would have large values because people would be interested in metal complexes that had relatively high formation constants if they wanted to use them for analytical purposes. Another thing to realize is that many ligands can form a series of stepwise complexes with a metal, as illustrated below.
\[\begin{align}
&\ce{M + L \leftrightarrow ML} &&\mathrm{K_{f1}}\nonumber\\
&\ce{ML + L \leftrightarrow ML_2} &&\mathrm{K_{f2}}\nonumber\\
&\ce{ML_2 + L \leftrightarrow ML_3} &&\mathrm{K_{f3}}\nonumber\\
&\ce{ML_3 + L \leftrightarrow ML_4} &&\mathrm{K_{f4}}\nonumber
\end{align}\nonumber\]
It is also worth examining what types of species function as ligands. First, it’s worth realizing that the metal in these reactions is almost always a cation. Therefore, anions are one group of compounds that have to be examined as possible ligands. The way to see if complexation occurs is to determine all of the anions and metal ions that exist in a particular solution, and then see if any possible combination of a metal ion with an anion has a value or values in the table of formation constants. If any do, then that process needs to be incorporated into any calculations of equilibrium concentrations. One thing to note is that every aqueous solution has some amount of hydroxide ion, and many metal ions form water-soluble complexes with hydroxide. The presence of hydroxide ion therefore provides an additional complication when assessing the distribution of most metal species in solution.
Another thing to realize is that anions are always the conjugate bases of acids. In other words, any anion has the potential to be protonated with a hydrogen ion. If the anion is the conjugate base of a strong acid (halide, nitrate, perchlorate), then its concentration will not vary as a function of pH because it will not be protonated in water. If the anion is the conjugate base of a weak acid, which is actually far more common, then the concentration of the anion in water is a function of the pH. This means that the complexation of the metal by the anion will depend on the pH as well. What you might begin to realize now is that metal complexation in water is a complicated process that is influenced by the pH and the availability of different ligands. We will see that there are a series of systematic ways to address metal complexation and handle all of the simultaneous equilibria that occur.
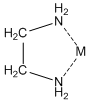
The other large group of ligands are the nitrogen bases. These are neutral ligands that have the ability to form donor-acceptor complexes with the metal ion. The ligand acts as an electron-pair donor, something we refer to as a Lewis base. The positive metal ion acts as an electron-pair acceptor, something we refer to as a Lewis acid. (Actually, the Lewis acid-Lewis base interaction also occurs for anions when they bond to metals). For example, ammonia is a ligand that forms water-soluble complexes with many metal ions. Ethylenediamine is another important nitrogen-containing ligand that forms water-soluble complexes with many metal ions. In this case, what is particularly interesting is that both nitrogen atoms bond to the metal ion at the same time, forming what is called a chelate complex.
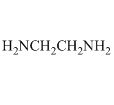
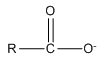
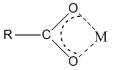
Anions can bond to metal ions in a chelate manner as well. For example, the carboxylate ion actually bonds to metal ions through a chelate arrangement of the two oxygen atoms.
Another very important ligand is the species ethylenediaminetetraacetic acid (H4EDTA or H4E). EDTA is a tetraprotic acid that can act as a ligand and form very stable chelate complexes with metal ions. We have a table of Kf values for different EDTA complexes and note that these are very large numbers. An interesting thing to realize is that we always think of the fully deprotonated ligand (E4–) as the species that actually forms the complex. The other forms (H4E, H3E–, H2E2–, HE3–) are not involved in the complexation. Note that this is a general observation. For example, in the phosphoric acid system, the species \(\ce{PO4^3-}\) would be the ligand, not the partially protonated \(\ce{HPO4^2-}\) and \(\ce{H2PO4^2-}\) species.
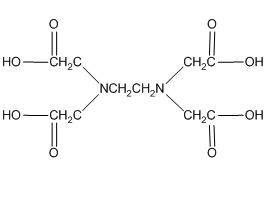
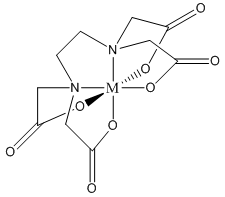
Note that one E4– ligand has the ability to completely surround a metal ion and fill all of the coordination sites simultaneously. It might be tempting to think that this ability to fill all the sites at one time accounts for the exceptionally large formation constants. In actuality, the large formation constants are driven more by entropy changes. If we think about the nature of a metal cation in water, we realize that the positive metal ion is surrounded by negative ends of water molecules as shown below. In this picture, the oxygen atoms of the water molecules are said to be in the first coordination sphere of the metal ion. This is typically what occurs with many metal salts in water. The cation and anion separate from each other and are solvated by water.
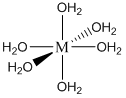
The reaction that we can now write to represent the bonding of E4– to a metal ion (M+) is shown below:
\[\ce{M(H2O)6+ + E^4- \leftrightarrow ME^3- + 6 H2O}\nonumber\]
Note that the reaction side of the equation has two species, the product side has seven species. There is considerably larger entropy associated with the seven species on the product side, and this huge gain in favorable entropy is what primarily accounts for the large formation constants of metal complexes with EDTA. We will rarely write the metal ion as \(\ce{M(H2O)6+}\) and instead simplify it to M+. But it’s sometimes worth remembering that it is surrounded by some number of water molecules. Also note that the ME3– species has a net charge of –3. Many of these water-soluble complexes have a net charge, which in part is responsible for their water solubility.
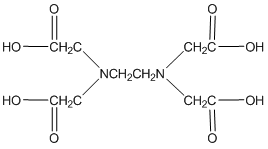
One last thing about EDTA. If you look in the structures shown in our table, you will see that EDTA is actually a zwitterion in solution (See below a neutral and zwitterionic form of EDTA). What’s important to realize is that it really does not matter what form you write it in. Both forms below have four dissociable protons. Both forms have a net neutral charge. Both can be expressed as H4EDTA.
.png?revision=1)
H4EDTA
(neutral)
.png?revision=1)
H4EDTA
(zwitterion)
In theory, it might actually be possible to protonate both nitrogen atoms of EDTA, producing a species of the form H6EDTA2+.
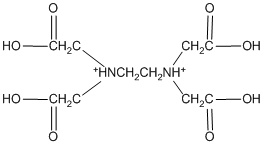
H6EDTA2+
This species does not occur because the first two protons are so acidic that, even if we dissolved EDTA in a strong acid such as concentrated hydrochloric acid, it is doubtful that these sites would be protonated. In water, at pH values of 1 or higher, we will never be able to put more than four protons onto the EDTA.
Now we are ready to calculate the answer to the first problem.
Calculate the concentration of free calcium(II) ion in a solution prepared with initial concentrations of calcium of 0.020 M and EDTA4- of 0.10 M.
In solving this problem, we will start under very naïve circumstances. We will not consider any other complexation of the calcium ion (for example, by something like hydroxide), and we have been given a concentration of E4– and do not need to worry about the pH of this solution, how we got a concentration of 0.10 M, or whether protonation occurs.
The first thing to do is to write the reaction and look up the relevant formation constant.
\[\ce{Ca^2+ + E^4- \leftrightarrow CaE^2-} \hspace{60px} \mathrm{K_f = 5.0\times 10^{10}}\nonumber\]
What we see is that has a very large formation constant. That means that this reaction will go to completion. The approach to solving this problem is to allow it to go to completion, realizing that one of the reagents will limit the amount of product that forms. Then we need to allow a small amount of back reaction to occur. We can construct the following chart.
\[\begin{align}
& &&\ce{Ca^2+}\hspace{25px} + &&\ce{E^4-} \hspace{25px}\leftrightarrow &&\ce{CaE^2-}\nonumber \\
&\ce{Initial} &&\mathrm{0.020\: M} &&\mathrm{0.10\: M} &&0\nonumber \\
&\ce{Complete\: Reaction} &&0 &&0.08 &&0.02\nonumber \\
&\ce{Back\: Reaction} &&\ce{x} &&0.08 +\ce{x} &&0.02 - \ce{x}\nonumber \\
&\ce{Assumption} && &&0.08 >>\ce{x} &&0.02 >>\ce{x}\nonumber
\end{align}\nonumber\]
The approximation that 0.08 >> x and 0.02 >> x is reasonable since the Kf value is so large, therefore the amount of back reaction will be excessively small.
\[\mathrm{K_f =\dfrac{[CaE^{2-}]}{[Ca^{2+}][E^{4-}]} =\dfrac{0.02}{(x)(0.08)} = 5.0\times10^{10}}\nonumber\]
\[\mathrm{x = [Ca^{2+}] = 5\times 10^{-12}}\nonumber\]
The amount of unreacted calcium ion is incredibly small. Obviously the approximations we made were justified and we see how far these reactions can go toward completion.
Contributors and Attributions
- Thomas Wenzel, Bates College (twenzel@bates.edu)
- Sourced from the Analytical Sciences Digital Library


