2. Calculate the concentration of free calcium(II) ions in a solution prepared with initial concentrations of calcium of 0.020 M and total EDTA of 0.10 M. The solution is buffered at a pH of 2.
Now we have added a complicating factor. We will incorporate the fact that the EDTA has several protonated forms, and that these forms depend on the pH of the solution. Since only the E4– form bonds to the metal ion, protonated forms of EDTA reduce the concentration of E4– available for complexation. If very little E4– is available for complexation, very little of the calcium ion will be complexed.
It is also worth realizing that, in most cases, we do know the pH of a solution. One reason is because we want a particular pH so we have prepared the solution in a buffer. The other is that it is very easy to measure the pH of a solution using a pH meter, so if pH is a relevant issue, we simply measure it.
The set of reactions below show what we now know will occur in this solution (note, we are ignoring the possibility that the calcium can complex with hydroxide ion – more on that later).
\[\begin{align}
\ce{Ca^2+ +\: &E^4- \leftrightarrow CaE^2- \\
&\:\:\Updownarrow\nonumber\\
&HE^3- \nonumber\\
&\:\:\Updownarrow\nonumber\\
&H2E^2- \nonumber\\
&\:\:\Updownarrow\nonumber\\
&H3E- \nonumber\\
&\:\:\Updownarrow\nonumber\\
&H4E\nonumber}
\end{align}\]
The problem we face here is that the reaction we want to examine is the Kf reaction for CaE2–. If we want to use our established way of doing that calculation, we need to know the initial amounts of Ca2+ and E4– that we have in solution, but some of the E4– has been protonated and we do not know how much we have. Also, we have one other problem. Suppose, in a solution with a total amount of EDTA of 0.10 M, we could calculate how much of the EDTA was in the E4– form. We could conceivably allow this to complex with the Ca2+, but we have an additional source of EDTA (the HE3–, H2E2–, H3E–, and H4E forms) that will redistribute to some extent and provide additional amounts of E4–.
There is a very interesting observation about acid-base systems. It turns out that if we know the pH of the solution, the fraction of the total that exists in any one form is fixed. In other words, the fraction of total EDTA that exists in the H4E, H3E–, H2E2–, HE3–, and E4– forms is only a function of the pH of the solution. It does not depend on the total amount of EDTA in solution. We refer to these fractions as α-values. We are usually interested in the α-value for the fully deprotonated anion, since that is the form that complexes with the metal. It’s important to realize that we can calculate α-values for any of the species involved in a series of reactions for a polyprotic acid.
It is worth showing that the fraction of EDTA that exists in solution as E4– is only a function of pH. This will also demonstrate the general procedure that we can use to calculate α-values.
First, write an expression for the fraction of EDTA that exists in solution as E4–.
\[\mathrm{α_{E^{4-}} =\dfrac{[E^{4-}]}{[H_4E] + [H_3E^-] + [H_2E^{2-}] + [HE^{3-}] + [E^{4-}]}}\]
Note that this is just the concentration of E4– over the total EDTA in solution. The next step is to take the reciprocal of this expression. Doing so will allow you to divide the equation into a set of separate terms.
\[\mathrm{\dfrac{1}{α_{E^{4-}}}=\dfrac{[H_4E]}{[E^{4-}]}+\dfrac{[H_3E^-]}{[E^{4-}]}+\dfrac{[H_2E^{2-}]}{[E^{4-}]}+\dfrac{[HE^{3-}]}{[E^{4-}]}+\dfrac{[E^{4-}]}{[E^{4-}]}}\]
The next step is to use the Ka values for EDTA to substitute in for each of the ratio terms. The first one to examine is the ratio of [HE3–]/[E4–], which we can obtain using only the Ka4 expression. Rearranging Ka4 as shown below gives the following term to substitute in.
\[\mathrm{HE^{3-} + H_2O \leftrightarrow E^{4-} + H_3O^+ \hspace{60px} K_{a4}}\]
\[\mathrm{K_{a4} =\dfrac{[E^{4-}][H_3O^+]}{[HE^{3-}]} \hspace{60px} \dfrac{[HE^{3-}]}{[E^{4-}]} =\dfrac{[H_3O^+]}{K_{a4}}}\]
Next we can evaluate an expression to substitute in for [H2E2–]/[E4–]. This will involve using the Ka3 and Ka4 expression for EDTA. The easiest way to see this is to add up the Ka3 and Ka4 reactions. Remember, the equilibrium constant for the resulting reaction is the product of the equilibrium constants for those added together.
\[\begin{align}
&\ce{H2E^2- + H2O \leftrightarrow HE^3- + H3O+} &&\mathrm{K_{a3}}\\
&\underline{\ce{HE^3- + H2O \leftrightarrow E^4- + H3O+}\hspace{20px}} &&\mathrm{K_{a4}}\nonumber\\
&\ce{H2E^2- + 2H2O \leftrightarrow E^4- + 2H3O+} &&\mathrm{K = K_{a3} K_{a4}}\nonumber
\end{align}\]
\[\mathrm{K_{a3} K_{a4} =\dfrac{[E^{4-}][H_3O^+]^2}{[H_2E^{2-}]} \hspace{60px} \dfrac{[H_2E^{2-}]}{[E^{4-}]} = \dfrac{[H_3O^+]^2}{K_{a3} K_{a4}}}\]
Perhaps by this point we see a pattern developing. Evaluating the [H3E–]/[E4–] term will require the use of Ka2, Ka3, and Ka4 and yield the following term:
\[\mathrm{\dfrac{[H_3E^-]}{[E^{4-}]} = \dfrac{[H_3O^+]^3}{K_{a2} K_{a3} K_{a4}}}\]
Similarly, evaluating the [H4E]/[E4–] term will, which requires using Ka1, Ka2, Ka3, and Ka4, will yield the following term:
\[\mathrm{\dfrac{[H_4E]}{[E^{4-}]} = \dfrac{[H_3O^+]^4}{K_{a1} K_{a2} K_{a3} K_{a4}}}\]
The final result is shown below.
\[\mathrm{\dfrac{1}{α_{E^{4-}}} = \dfrac{[H_3O^+]^4}{K_{a1} K_{a2} K_{a3} K_{a4}} + \dfrac{[H_3O^+]^3}{K_{a2} K_{a3} K_{a4}} + \dfrac{[H_3O^+]^2}{K_{a3} K_{a4}} + \dfrac{[H_3O^+]}{K_{a4}} + 1}\]
What we see is that the only variable in this expression is [H3O+], so the fraction of EDTA that exists in solution as E4– is only a function of the pH. There is no term for the total amount of EDTA in the equation, so that does not matter. It only depends on the pH.
Similarly, we can evaluate the fraction of the other species as a function of pH. For example, let’s begin the process of evaluating the α-value of H4E. The general procedure is the same as used for \(\mathrm{α_{E^{4-}}}\). The first step is to write the relevant equation for H4E over the total.
\[\mathrm{α_{H_4E} =\dfrac{[H_4E]}{[H_4E] + [H_3E^-] + [H_2E^{2-}] + [HE^{3-}] + [E^{4-}]}}\]
The next step is to take the reciprocal and divide the equation into separate terms.
\[\mathrm{\dfrac{1}{α_{H_4E}}=\dfrac{[H_4E]}{[H_4E]} + \dfrac{[H_3E^-]}{[H_4E]} + \dfrac{[H_2E^{2-}]}{[H_4E]} + \dfrac{[HE^{3-}]}{[H_4E]} + \dfrac{[E^{4-}]}{[H_4E]}}\]
The next step is to use the Ka expressions to express each ratio in terms of [H3O+] and the Ka values. I will not show all these rearrangements here, but doing them yields the following result for 1/\(\mathrm{α_{H_4E}}\). You ought to try this and convince yourself that this is correct.
\[\mathrm{\dfrac{1}{α_{H_4E}}= 1 +\dfrac{K_{a1}}{[H_3O^+]} + \dfrac{K_{a1} K_{a2}}{[H_3O^+]^2} +\dfrac{K_{a1} K_{a2} K_{a3}}{[H_3O^+]^3} + \dfrac{K_{a1} K_{a2} K_{a3} K_{a4}}{[H_3O^+]^4}}\]
Similarly, we could write expressions, take reciprocals, and evaluate the terms for α-values for H3E–, H2E2–, and HE3–. The full 1/α-value expressions that would result for all of the species involved in the EDTA system are shown below. Note the characteristic patterns that result.
\[\mathrm{\dfrac{1}{α_{E^{4-}}}= \dfrac{[H_3O^+]^4}{K_{a1}K_{a2}K_{a3}K_{a4}} + \dfrac{[H_3O^+]^3}{K_{a2}K_{a3}K_{a4}} +\dfrac{[H_3O^+]^2}{K_{a3}K_{a4}} + \dfrac{[H_3O^+]}{K_{a4}}+1 }\]
\[\mathrm{\dfrac{1}{α_{HE^{3-}}}= \dfrac{[H_3O^+]^3}{K_{a1}K_{a2}K_{a3}} + \dfrac{[H_3O^+]^2}{K_{a2}K_{a3}} +\dfrac{[H_3O^+]}{K_{a3}} +1 + \dfrac{K_{a4}}{[H_3O^+]} }\]
\[\mathrm{\dfrac{1}{α_{H_2E^{2-}}}= \dfrac{[H_3O^+]^2}{K_{a1}K_{a2}} + \dfrac{[H_3O^+]}{K_{a2}}+1 +\dfrac{K_{a3}}{[H_3O^+]} + \dfrac{K_{a3}K_{a4}}{[H_3O^+]^2} }\]
\[\mathrm{\dfrac{1}{α_{H_3E^-}}= \dfrac{[H_3O^+]}{K_{a1}} +1 + \dfrac{K_{a2}}{[H_3O^+]} +\dfrac{K_{a2}K_{a3}}{[H_3O^+]^2} + \dfrac{K_{a2}K_{a3}K_{a4}}{[H_3O^+]^3} }\]
\[\mathrm{\dfrac{1}{α_{H_4E}}= 1 + \dfrac{K_{a1}}{[H_3O^+]} +\dfrac{K_{a1}K_{a2}}{[H_3O^+]^2} + \dfrac{K_{a1}K_{a2}K_{a3}}{[H_3O^+]^3} + \dfrac{K_{a1}K_{a2}K_{a3}K_{a4}}{[H_3O^+]^4}}\]
The other important thing to do with α-values is examine a plot of α-values versus pH for a series of compounds. Examples are shown in Figure 5 for carbonic acid, phosphoric acid, and citric acid.
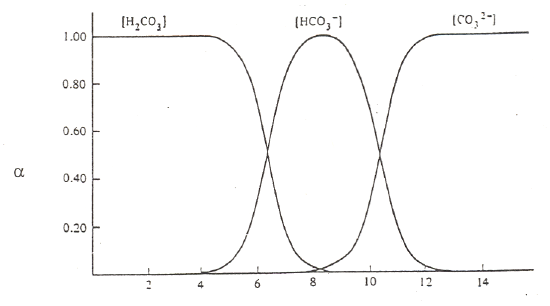
Carbonic Acid (pKa values of 6.4 and 10.4)
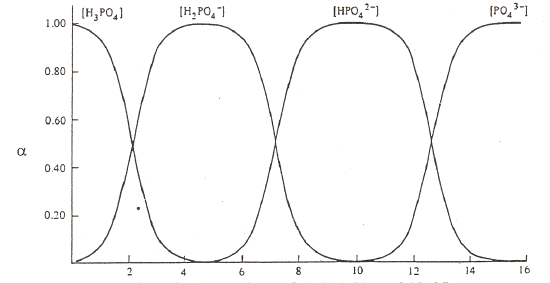
Phosphoric Acid (pKa values of 2.12, 7.21, and 12.66)
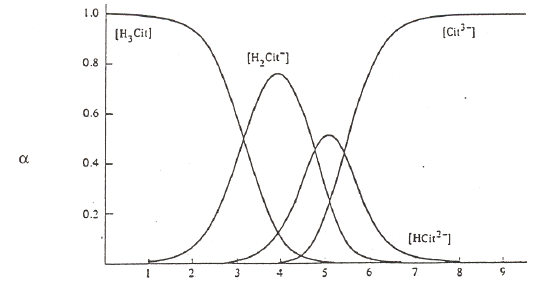
Citric Acid (pKa values of 3.13, 4.76, and 5.41)
Figure 5. Plots of α-values as a function of pH for carbonic, phosphoric and citric acid.
There are several important items to note about these figures on the previous page. At very low pH, meaning highly acidic conditions, the fully protonated forms predominate. At very high pH, meaning highly basic conditions, the fully deprotonated forms predominate. Since the deprotonated forms are the ones that will bond to metal ions, complexation of metal ions by ligands is favored at more basic pH values. (Note, we could do a similar plot of α-values for the different forms of ethylenediamine, H2En2+, HEn+, and En. Remembering that the neutral form, En, is the one that complexes with metals, we would see that this form is favored at more basic pH values). At intermediate pH values, different intermediate forms increase and then diminish as the pH is raised from acidic to basic conditions. At the crossing points of two of the α-value plots, we typically have a 50:50 mixture of a conjugate pair. In other words, these crossing points are the excellent buffer regions for these reagents.
Observe that the forms of the carbonic and phosphoric acid systems are very regularized. There is some pH where only one species of the series predominates and the concentrations of all others are minimal. This is not the case with citric acid. We see a somewhat unusual situation in which at a pH of around 4 and 5, we see that the H2cit– and Hcit2– forms respectively do not reach 99%. At these points we find appreciable amounts of the neighboring species. Also note that the amounts of H2cit– and cit3– present at the point at which Hcit2– is maximized are exactly equal to each other. The same thing occurs for the two neighboring species at pH 4. This is a rather rare occasion of having appreciable quantities of three species from an acid-base system present at the same time. The reason for this unusual behavior is that the pKa values are very close to each other. (Note: pKa3 in this chart is reportedly 5.41, which is different than the value of 6.396 in our table of K values!) We have already examined citric acid when it was titrated with sodium hydroxide and introduced its somewhat unusual behavior. The plot of α-values really points out the effects of having close pKa values and how this influences the concentrations of species in solution.
We are now in a position to finally see how to incorporate an α-value into the calculation involving complexation of Ca2+ by E4– at a pH of 2. Write the formation constant expression and recognize that we can substitute in for the [E4–] term.
\[\ce{Ca^2+ + E^4- \leftrightarrow CaE^2-}\hspace{60px} \mathrm{K_f}\]
\[\mathrm{K_f =\dfrac{[CaE^{2-}]}{[Ca^{2+}][E^{4-}]}}\]
\[\mathrm{[E^{4-}] =α_{E^{4-}}[E]_{TOT}}\]
Substituting the [E4–] expression into the Kf equation gives the following:
\[\mathrm{K_f =\dfrac{[CaE^{2-}]}{[Ca^{2+}]α_{E^{4-}}[E]_{TOT}}}\]
The \(\mathrm{α_{E^{4-}}}\) term is a constant, since the pH is known, and we can rearrange the expression into the following:
\[\mathrm{(K_f)(α_{E^{4-}}) =\dfrac{[CaE^{2-}]}{[Ca^{2+}][E]_{TOT}}}\]
\(\mathrm{(K_f)(α_{E^{4-}})}\) is something we call a conditional constant (KCOND). Why a conditional constant? It turns out that the pH is a “condition” in this solution that influences the concentration and availability of E4–. Incorporating the α-value into the conditional constant will allow us to assess whether it is likely that the Ca2+ will complex with the E4–. The conditional constants for the complexation of Ca2+ with E4– are shown in Table 6 as a function of pH. What we need to do is calculate the conditional constant, and then examine its magnitude. If the conditional constant is large, the reaction goes to completion. If the conditional constant is small, the reaction does not go to completion.
Table 6. Conditional constants for the complexation of Ca2+ with E4-.
| pH |
\(\mathrm{α_{E^{4-}}}\) |
\(\mathrm{(K_f)(α_{E^{4-}})}\) |
Extent of reaction |
| 1 |
3.66×10-18 |
1.83×10-7 |
Very small |
| 2 |
2.00×10-14 |
1.00×10-3 |
Fairly small |
| 3 |
1.61×10-11 |
0.805 |
Intermediate |
| 4 |
2.48×10-9 |
1.24×102 |
Intermediate |
| 5 |
2.47×10-7 |
1.24×104 |
Close to completion |
| 6 |
1.67×10-5 |
8.35×106 |
Completion |
| 7 |
3.89×10-4 |
1.95×107 |
Completion |
| 8 |
4.47×10-3 |
2.24×108 |
Completion |
| 9 |
4.36×10-2 |
2.18×109 |
Completion |
| 10 |
0.314 |
1.57×1010 |
Completion |
| 11 |
0.820 |
4.10×1010 |
Completion |
| 12 |
0.979 |
4.90×1010 |
Completion |
| 13 |
0.998 |
4.99×1010 |
Completion |
Note how the reaction, based on the magnitude of the conditional constant, goes further to completion as the pH is made more basic. At very acidic pH values, very little reaction occurs. Also note that the conditional constant is large by a pH of 6, even though the α-value for the E4– is still fairly small (1.67×10-5). This shows how the very large formation constant (5×1010) leads to formation of the complex (as the E4– is used up, we have a source of additional E4– from the protonated E species HE3–, H2E2–, H3E–, and H4E). But also note, the α-values for the E species do not change as long as the pH remains fixed. If E4– is removed by complexation, some new E4– will form to maintain the same distribution of α-values for all of the E species.
If we have the expression:
\[\mathrm{(K_f)(α_{E^{4-}}) =\dfrac{[CaE^{2-}]}{[Ca^{2+}][E]_{TOT}}}\]
We could write this as belonging to the following reaction. Note that the procedure we use assumes that only a small amount of reaction occurs since the conditional constant is only 1×10-3.
\[\begin{align}
& &&\ce{Ca^2+}\hspace{25px} + &&\ce{E_{TOT}} \hspace{25px}\leftrightarrow &&\ce{CaE^2-} &&\mathrm{K_{COND} = (K_f)(α_{E^{4-}}) = 1\times 10^{-3}} \\
&\ce{Initial} &&0.02 &&0.10 &&0 && \nonumber\\
&\ce{Equilibrium} &&0.02 - \ce{x} &&0.10 - \ce{x} &&\ce{x} && \nonumber\\
&\ce{Approximation} &&0.02 &&0.10 &&\ce{x} &&\nonumber
\end{align}\]
Substitute these in to calculate the value of [CaE2–]:
\[\mathrm{K_{COND} = \dfrac{[CaE^{2-}]}{[Ca^{2+}][E]_{TOT}} =\dfrac{x}{(0.02)(0.1)} = 1\times10^{-3}}\]
\[\mathrm{x = [CaE^{2-}] = 2\times 10^{-6}}\]
Checking the approximation shows that it was valid to assume that very little of the Ca2+ and E4– complexes.
\[\dfrac{2×10^{-6}}{0.02} × 100 = 0.01\%\]
Let’s also consider how we would handle this if we had a pH with a large conditional constant. For example, consider the situation at pH 6. In this case, we treat it assuming that the reaction goes to completion and that some back reaction then occurs.
\[\begin{align}
& &&\ce{Ca^2+}\hspace{25px} + &&\ce{E_{TOT}} \hspace{25px}\leftrightarrow &&\ce{CaE^2-} &&\mathrm{K_{COND} =8.35\times 10^6} \\
&\ce{Initial} &&0.02 &&0.10 &&0 && \nonumber\\
&\ce{Completion} &&0 &&0.08 &&0.02 && \nonumber\\
&\ce{Back\: reaction} &&\ce{x} &&0.08 + \ce{x} &&0.02 - \ce{x} && \nonumber\\
&\ce{Approximation} &&\ce{x} &&0.08 &&0.02 &&\nonumber
\end{align}\]
Substituting this in gives the following concentration of free calcium ion. This concentration is very low such that we know the approximations were valid.
\[\mathrm{K_{COND} =\dfrac{[CaE^{2-}]}{[Ca^{2+}][E]_{TOT}} =\dfrac{0.02}{(x)(0.08)} = 8.35×10^6}\]
\[\mathrm{x = [Ca^{2+}] = 2.99\times 10^{-8}}\]
An important thing to notice is that the total concentration of EDTA drops in this process because some of it reacts with the Ca2+ to form the complex. Remember that [E]TOT refers only to those forms of EDTA that are not complexed with Ca2+ and does not include the complexed form (CaE2–).





