3: UV Spectroscopy

Last updated
Save as PDF

Page ID: 332803

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

UV Spectroscopy

Which electrons can be excited? Where do they go?

In order to absorb UV-Vis light, the molecule must contain a chromophore—the part of a molecule that absorbs UV light.

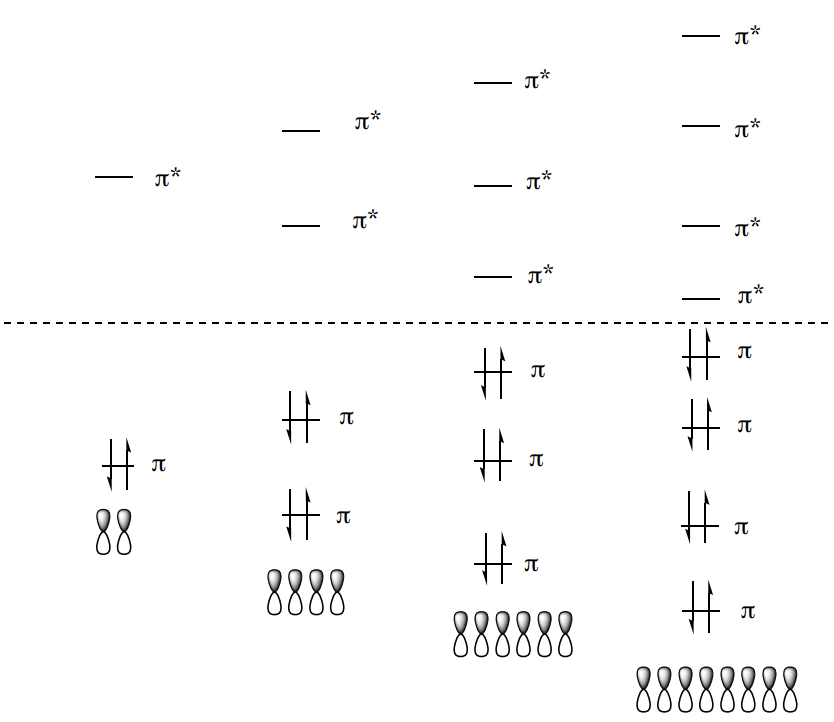
An MO diagram for formaldehyde (methanol, CH2O) is shown.

Place the proper number of electrons in the diagram.

There are 4 common types of transitions (n-$\pi$*, $\pi$-$\pi$*, $\sigma$-$\sigma$*, n-$\sigma$*) for organic compounds

What structural features must be present for each type of transition?
- $\sigma \rightarrow \sigma$*
- $\pi \rightarrow \pi$*
- $n \rightarrow \pi$*
- $n \rightarrow \sigma$*
Propose transition types for the list of functional groups below:
- Alkane
- Alkene
- Alkyne
- Alcohol
- Carbonyl
- Amine
- Nitrile
Molecules with chromophores tend to have a lot of pi bonds. Explain why.

Table of wavelengths and extinction coefficients ($\epsilon_{max}$) for those transitions
Transition	~$\lambda_{max}$ (nm)	$\epsilon_{max}$
$\sigma \rightarrow \sigma$*	135	v. small
$\pi \rightarrow \pi$*	160-280	2,400-25,000
$n \rightarrow \pi$*	279-320	10-50
$n \rightarrow \sigma$*	160-250	100-7,000

Why are the $\lambda_{max}$ values shown as ranges and not discrete numbers?
Using the MO energy diagram, explain the relative energies of the transitions.

Extinction Coefficients

Beer’s law states that the absorbance of a solution is proportional to its concentration. Mathematically, Beer’s law is

\[A = \epsilon b c\]

A is the absorbance of the solution

$\epsilon$ is the quantity called the molar absorptivity

b is the path length in cm of the solution cell

c is the solution concentration (molarity)

Absorbance spectra are usually gathered as a function of wavelength. Absorbance is dependent upon concentration.

Suppose that a UV absorbance spectrum was obtained for a solution of a compound. Then the concentration of the solution was doubled. Redraw the new spectrum on the same scale.

Absorbance is also dependent the molar absorptivity. Molar absorptivity ($\epsilon$) tells you how likely an electronic transition is.

The more likely a particular absorbance occurs, then the [ smaller / larger ] the $\epsilon$ will be.
If an electronic transition is difficult, _______ [ more / fewer ] electrons will be excited, and the $\epsilon$ will ________ [ decrease / increase ] and the apparent intensity will be weaker.
$\sigma \rightarrow \sigma$* has a small extinction coefficient. Why?
$n \rightarrow \pi$* are the lowest energy of any transitions we observe and consequently have the longest wavelength. However, they typically have the smallest extinction coefficient. Why is the $n \rightarrow \pi$* transition so difficult even though the energy gap is small? Consider how much orbital overlap is present.

UV Spectroscopy: Analysis

UV-Vis Spectroscopy is useful in the laboratory for several purposes.

Determination of structure.
Determination of the concentration of a known sample

UV-Vis Spectroscopy: Determination of structure

The molecules most likely to absorb light in the UV-Vis region are structures with pi bonds. This severely limits the use of UV-Vis as a general method for determining structure.

Additionally, molecules with an isolated alkene tend to have $\lambda_{max}$ around 170-190 nm which is not measure by most instruments.

With conjugation, the $\pi \rightarrow \pi$* orbitals are [ closer or further ] apart.

Conjugated systems require [ higher or lower ] energy to excite an electron.
However, generally moves the absorption maxima to [ longer or shorter] wavelengths.

Thus, conjugation becomes the major structural feature identified by this technique.

Determination of Structure: Predicting $\lambda_{max}$ of Conjugated Compounds There are some standardized rules for predicting the $\lambda_{max}$ in conjugated molecules called the Woodward-Fieser Rules.

Core Chromophore	Substituent	Influence
Trans diene: 215 nm	Alkyl	+5
	Alkoxy	+6
	Halide	+10
Cis diene: 260 nm	Acyl	0
	Amino	60
	Another double bond	+30
	Phenyl	+60

*Each exocyclic double bond adds 5 nm.

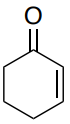
Predict the have $\lambda_{max}$ for the following compounds.

Base (cis or trans): _______

5 alkyl group substituents _______

2 exocyclic bonds _______

Additional double bond _______

Total: _______ Compare to actual: 283 nm

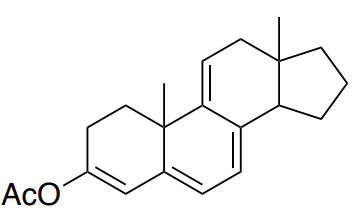
Base (cis or trans): _______

4 alkyl group substituents _______

2 exocyclic bonds _______

Additional double bond _______

Total: _______ Compare to actual: 355 nm

Determination of Structure:

Predicting $\lambda_{max}$ of Conjugated Carbonyl Compounds The Woodward-Fieser Rules also extend to conjugated carbonyl compounds.

Core Chromophore	Substituent	$\alpha$-Influence	$\beta$-Influence
Acyclic enone: 215 nm	Alkyl	+10	+12
Acyclic enone: 215 nm	Alkoxy/Hydroxyl	+35	+30
Cyclic hexenone: 215 nm	Chloro	+15	+12
	Bromo	+25	+30
	Acyl	+6	+6
Cyclic pentenone: 202 nm	Another double bond	+30
Cyclic pentenone: 202 nm	Phenyl	+60

*Each exocyclic double bond adds 5 nm.

** In water, add 8 nm.

• Predict the have $\lambda_{max}$ for the following compounds.

Base (cis or trans): _______

1 alpha alkyl group substituents _______

2 beta alkyl group substituents _______

Additional double bond _______

Total: _______ Compare to actual: 249 nm

Base (cis or trans): _______

alpha bromo group substituents _______

2 beta alkyl group substituents _______

Additional double bond _______

Total: _______ Compare to actual: 251 nm

There are lots of tables for use in predicting values. There are also databases of known UV spectra for direct comparison.

UV-Vis Spectroscopy: Determination of the concentration of a known sample

Beer's Law: $A = \epsilon b c$

A is the absorbance of the solution

$\epsilon$ is the quantity called the molar absorptivity

b is the path length in cm of the solution cell

c is the solution concentration (molarity)

Explain how you could determine the concentration of a sample using Beer’s Law. Show the math.

The literature value of ε for 1,3-pentadiene in hexane is 26,000 (mol / L)^-¹cm^-1 at its maximum absorbance at 224 nm. You obtain a 10 mL sample and take a UV spectrum in a cell with a 1 cm path length, finding that A₂₂₄ = 0.850.

What is the concentration (molarity) of the solution? Show your work.
How many grams of 1,3 pentadiene (molar mass = 68 g/mol) are in the solution?

UV Spectroscopy: Solvent Choices

Solvents used for UV Spectroscopy Samples

What solvents (list solvents with structures) would interfere with UV analysis?

Solvent	Structure
Acetic acid (AcOH)
Acetone
Benzene (PhH)
tert-Butyl methyl ether
Chloroform
Diethyl ether
Dimethyl formamide
Dimethyl sulfoxide (DMSO)
Ethyl acetate (EtOAc)
Hexane
Octane
Tetrahydrofuran (THF)
Toluene (PhMe)
Water

Not everything is soluble in hexane/octane, what range of wavelengths can you measure using methanol as your solvent?

Practice Problem

It is often important to be able to quantify the amount of protein in a solution. One method is based on the fact that aromatic amino acids tyrosine (Tyr) and tryptophan (Trp) absorb ultraviolet light maximally at ~280 nm. The amino acid cysteine does not absorb at this wavelength; however, two cysteines may react with each other to form a disulfide (S-S) linkage which is called cystine and this structural feature does. The general method is to just take a solution of unknown protein sample, stick it into a spectrophotometer, and read the A₂₈₀.

Based on a sample of measured molar extinction coefficient (ε) values for 80 proteins, the ε at 280 nm of a folded protein in water, ε(280), can best be predicted with this equation:

\[\epsilon(@ 280) (\text{M$^{-1}$cm$^{-1}$}) = (\#Trp)(5,500) + (\#Tyr)(1,490) + (\#cystine)(125) \]

Of course, it is necessary to know the structure of the protein so that the number of each type of amino acid residue can be entered into the equation.

Examine the equation and predict the type of absorption that each of the three amino acids in the equation undergoes at 280 nm.
Draw the side chains of these three amino acids.
Does this match your prediction? Explain.

Search

Text Color

Text Size

Margin Size

Font Type

Transition	~\(\lambda_{max}\) (nm)	\(\epsilon_{max}\)
\(\sigma \rightarrow \sigma\)*	135	v. small
\(\pi \rightarrow \pi\)*	160-280	2,400-25,000
\(n \rightarrow \pi\)*	279-320	10-50
\(n \rightarrow \sigma\)*	160-250	100-7,000