2.2: Lab - Units, Measurements, and Significant Figures
- Page ID
- 438406
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Equipment and Materials
Prepare 12 sets of equipment and materials for 24 students per class section. Include a few more for backup if needed. Each set should include
Equipment
- Meter stick, metric ruler (hundredths and tenths) and inch ruler
- Solid rectangular metal pieces for dimensions measurements
- These solid rectangular objects should be able to fit in a 100-mL graduated cylinders
- Mass or Analytical Balance
- Weigh boats
- 250-mL beaker, 250-mL Erlenmeyer flask, and a 50-mL graduated cylinders
- Feet Samples (Already in Lab)
Materials
Distilled Water
- Fill a 25-mL graduated cylinder with about 10 mL of faintly colored water (use food coloring)
- Fill a 50-mL graduated cylinder with about 25 mL of faintly colored water (use food coloring)
- Fill a 100-mL graduated cylinder with about 50 mL of faintly colored water (use food coloring)
- Measure and report mass, length and volume of objects with correct significant figures
- Perform calculations with the correct number of significant figures
- Explore the importance of measurements in healthcare
- Determine medication dosage and related problems based on measurements
- Determine the real life impact of error in measurements and calculations
- Recognize the type of function of different glassware used for measurements
Laboratory Skill
- Practice using and reading an electronic balance
- Practice using and reading measurements in graduated cylinder
- Practice using and reading a metric and inch ruler
- Practice using and reading measurements in burets and beakers
Equipment and Materials
- Meter stick, metric ruler (hundredths and tenths) and inch ruler
- Solid rectangular metal pieces for dimensions measurements
- Distilled water
- 250-mL beaker, 250-mL Erlenmeyer flask, and a 50-mL graduated
Safety and Hazard Information
N/A
Background Information
Measurements are central to the development of experiments and scientific theories. Measurements are critical to the chemical, farming, engineering, and health care industries. For example, hospital diagnosis and medication administration are solely based on vital signs or precise measurement of key health parameters (weight, height, body temperature, blood pressure). In measurements, devices are used to determine properties/quantities of an object by comparing them to a standard. In science and clinical settings, the metric unit system is the most common system of measurement. Unfortunately, measurements are never 100% precise or accurate, leading to uncertainty or errors associated with the measuring device, process, or person doing the measurement. The appropriate number of digits reported in measurements is called significant figures and describes this uncertainty in measurements. The relation between error and the appropriate number of significant figures (digits) recorded for each laboratory instrument or glassware used will be explored in these laboratory exercises.
Units of Measurement
You may be more familiar with measurements like 40 yards, 98\(^{\circ}\)F and 25 lbs because these units are common in the US system of measurements. The metric system of units is common to chemistry and other sciences (Table \(\PageIndex{A}\)).
Table \(\PageIndex{A}\): Sample unit of measurements, unit abbreviations and tools used to carry out measurements
| Measurement | Metric Unit | SI Unit | US system of Units | Measuring Device |
|---|---|---|---|---|
| Length | Meter (m), centimeter (cm) | Meter (m) | Mile (mi), yard (yd) | Ruler |
| Volume | Liters (L), milliliters (mL) | Cubic meter (m\(^3\)) | Gallon (gal), cup | Graduated cylinder |
| Mass | Grams (g) | Kilogram (kg) | Pound (lbs) | Scale/Balance |
| Temperature | Degree Celsius (\(^{\circ}\)C) | Kelvin (K) | Degree Fahrenheit (\(^{\circ}\)F) | Thermometer |
Making Measurements and Significant Figures
All measured numbers have some degree of uncertainty. This uncertainty is reflected in the appropriate number of significant figures reported. Significant figures in any measurement are digits that are known with certainty, plus one additional digit whose accuracy is uncertain (estimated).
Volume Measurements
Volume is the amount of space occupied by an object. In this section, you will learn how to carefully make volume measurements. Many reactions in chemistry involve transferring differing quantities of liquid solutions. It is therefore import to learn about the appropriate glassware needed to measure volume of liquids, and how to correctly read volume from the glassware (See Figure \(\PageIndex{1}\)).
How to use a graduated cylinder?
1. Look straight across at the graduated cylinder to avoid parallax error (Figure \(\PageIndex{2}\)). Read the bottom of the meniscus (the curved surface of the solution).
2. Important note about significant digits: A 100 mL graduated cylinder has marks at 1-mL intervals; therefore, you should estimate the volume to the nearest 0.1 mL. This is done by dividing the space between the 1-mL marks into ten imaginary spaces and deciding which of those spaces the meniscus is closest to. It’s OK if you aren’t sure—use your best judgment. The last digit of any measurement is supposed to be uncertain or an estimate or best guessed number.
3. If the meniscus is exactly on a line, you still record the volume to the nearest 0.1 mL. For example, if it’s right on the 27-mL line, record the volume as "27.0 mL" to show that you read it carefully and the margin of error is 0.1 mL. Remember, trailing zeros after the decimal point are significant.

Length Measurements
Length measures how tall, wide, or long an object is, using a ruler or meter stick. The diameter of the retina of an eye or height measurements can help doctors determine underlying health problems. Length can be measured in centimeters, meters, millimeters, miles, inches etc.
How to use a ruler or meter stick?
Use a metric ruler to measure the length of objects as shown in Figure \(\PageIndex{3}\). The largest hash marks represent 1 cm lengths. The second largest marks represent 0.5 cm lengths. The smallest marks represent 0.1 cm or 1 mm lengths. This implies we can confidently record measurements to the 0.1 cm and therefore our estimated digit will be in the hundredth’s place (0.01 cm). The length of the rectangle using this metric ruler is correctly recorded as 4.55 cm, but 4.54, 4.56 cm or 4.57 would also be acceptable.

Similarly, use an inch ruler to measure the length of objects as shown in Figure \(\PageIndex{4}\). The largest marks represent 1 inch lengths. The second largest marks represent 0.5 or 1/2 inch lengths. The third marks represent 1/4 or 3/4 inch lengths and the smallest 1/8 or 7/8 inch lengths. For measurements in decimal places, use an estimated digit in the hundredth’s place (0.01). The length of the candy using this inch ruler is correctly recorded as 6 1/2 or 6.50 in.

Mass Measurements
Mass describes the amount of material (atoms, molecules, etc) an object contains. Mass is measured in the lab using an electronic balance.
How to use an electronic balance?
1. Take your object to a balance.
2. Set a weigh boat on the pan of the balance.
3. Press the Tare button to zero the weigh boat.
4. Place your object in the weigh boat, read the mass and record in your report sheet.
5. Record all of the digits including trailing zeros. For example, if your object weighs 185.000 g and you write "185 g" it is wrong! Trailing zeros after the decimal point are significant digits. "185 g" means the margin of error is \(\pm\)1 g. That is to the ones place and your estimated digit is 5. "185.000 g" means the margin of error is \(\pm\)0.001 g. That is to the thousandth place and your estimated digit is the last 0.
The balances we use are usually precise to 0.001 g (thousandth) so all masses should be recorded to the third decimal place (Figure \(\PageIndex{5}\)). Note that for large items and glassware you do not need a weigh boat. Weigh boats are used to contain and determine the mass of liquid or solid chemicals.

Significant Figures in Calculations
The results of a calculation involving measurements can only be as good as the least accurate measurement used in the calculations. In other words, a chain is only as strong as its weakest link. For example, imagine using the two rulers shown in Figure \(\PageIndex{6}\) below to measure the length and width of a rectangular object. Length and width are the parameters that are needed to determine area and perimeter of the object. The number of significant figures in the final answer depends on both the number of significant figures in the measurements and on the mathematical operation.

The measurement of length with the ruler on the left will be recorded as 4.56 cm and the width with ruler on the right as 3.0 cm.
For addition and subtraction, your calculated value can only have the same number of decimal places as the measurement with the fewest number of decimal places.
Suppose you now want to calculate the perimeter: L+W+L+W. or \(2 \cdot (\)L+W)
You will first perform the calculation:
4.56 cm + 4.56 cm + 3.0 cm + 3.0 cm = 15.12 cm
Since the least precise measurement has only 1 place after the decimal, your calculation must be cut off after the first position to the right of the decimal by rounding down or up:
4.56 cm + 4.56 cm + 3.0 cm + 3.0 cm = 15.1 cm
For multiplication and division, the result of a calculation involving measurements has the same number of significant figures as the measurement with the fewest number of significant figures.
Suppose you now want to calculate the area: L\(\cdot\)W
You will first perform the calculation:
4.56 cm \(\cdot\) 3.0 cm = 13.68 cm\(^2\)
Since 3.0 cm has only 2 significant figures as opposed to 3 significant figures for 4.56 cm, the result of the multiplication needs to be reported to only 2 significant figures. Your calculation must be cut off after the 2nd measured digit by rounding down or up:
4.56 cm \(\cdot\) 3.0 cm = 14 cm\(^2\)
Experimental
\(\PageIndex{A}\): Volume from Graduated Cylinder
Materials
10-mL Graduated Cylinder
50-mL Graduated Cylinder
100-mL graduated Cylinder
Procedure
1. Test your volume measurement skills by correctly estimating the volume of three provided unknown liquids in the lab. Be sure to use the correct number of significant figures. Record your data in Data Table \(\PageIndex{1}\).
\(\PageIndex{B}\): Measuring Glassware Lengths
Materials
250-mL Beaker
250-mL Erlenmeyer flask
100-mL graduated cylinder
Procedures
1. Measure the height of each piece of glassware in both cm and inches.
2. To ensure consistency use two meter stick, with one placed flat on the top of the glassware and the other ruler perpendicular to obtain the height of the object.
3. For measurements in inches, convert the fractional part of the number into a decimal and record the value in inches with 2 decimal places (Example: 8 1/4 inches becomes 8.25 inches).
4. Record all values in Data Table \(\PageIndex{2}\).
5. Immediately to the right of each measured value you record, write the number of significant figures in that recorded value in the SF column.
6. For each pair of measurements, divide the Height in cm by the Height in inches.
7. Complete all questions related to Data Table \(\PageIndex{2}\). Check all values to ensure that you are including the correct number of significant figures.
8. In this section you will also measure the length of feet for three different babies and then record in Data Table \(\PageIndex{3}\).
9. Use the foot length and mass graph to estimate the weight of the baby and provide diagnosis of whether the baby is preterm or term.
\(\PageIndex{C}\): Measuring Volume of a Solid
Materials
100-mL graduated cylinder
Solid rectangular object
Procedure
The volume of a solid object with a rectangular shape can be calculated by measuring the dimensions of the object.
1. Measure the height (H), width (W), and length (L) of the solid rectangular object in cm. Record your values with the correct number of SF.
2. Multiply L \(\times\) W \(\times\) H to find the volume of the solid. When you multiply these values, you must multiply both the numbers and the units. Record your answer.
The volume of a solid object with an irregular shape can be determined through volume displacement.
1. Using a 100-mL graduated cylinder, fill the graduated cylinder to approximately 50 mL with tap water and record the volume to the correct number of significant figures.
2. Take the same metal object that you just measured for volume and carefully place the object in the graduated cylinder.
3. Record the new volume of the water.
4. Based on the final volume of the water and the initial volume of the water, calculate the volume of the object.
\(\PageIndex{D}\): Measuring Mass and Volume of Water with Beaker
Materials
50-mL beaker (\(n = 1\))
Procedure
1. Measure the mass of the beaker and record the mass in the space above Data Table \(\PageIndex{4}\).
2. Fill the beaker with 25 mL of tap water.
3. Read the measurement for the volume of water as accurately as possible and record in Data Table \(\PageIndex{4}\).
4. Measure the total mass of the beaker with water.
5. Calculate the mass of water by subtracting the mass of the beaker from the total mass (beaker + water).
6. Record the mass of water in Data Table \(\PageIndex{4}\).
7. Empty the water from the beaker in the sink.
8. Repeat steps 2-7 for a total of three trials.
9. Using the data you recorded in Data Table \(\PageIndex{4}\), calculate using Excel the Mean and Standard Deviation Values (Refer to your Excel lab) for Mass for each of the 3 trials for the Beaker. Record those values in Data Table \(\PageIndex{4}\).
\(\PageIndex{E}\): Measuring Mass and Volume of Water with Graduated Cylinder
Materials
50-mL Graduated Cylinder (\(n = 1\))
Procedure
1. Measure the mass of a 50-mL graduated cylinder and record the mass in the space above Data Table \(\PageIndex{5}\).
2. Fill the graduated cylinder with 25 mL of tap water.
3. Read the measurement for the volume of water as accurately as possible and record in Data Table \(\PageIndex{5}\).
4. Measure the total mass of the graduated cylinder with water.
5. Calculate the mass of water by subtracting the mass of the graduated cylinder from the total mass (graduated cylinder + water).
6. Record the mass of water in Data Table \(\PageIndex{5}\).
7. Empty the water from the graduated cylinder in the sink.
8. Repeat steps 2-7 for a total of three trials.
9. Using the data you recorded in Data Table \(\PageIndex{5}\), calculate using Excel the Mean and Standard Deviation Values (Refer to your Excel lab) for Mass for each of the 3 trials for the graduated cylinder. Record those values in Data Table \(\PageIndex{5}\).
Experimental Report
| Date: | Name: |
| Section: | Team: |
| Instructor: |
\(\PageIndex{A}\) Volume from Graduated Cylinder
Data Table \(\PageIndex{1}\)
| Sample | Volume (mL) |
|---|---|
| 1 | |
| 2 | |
| 3 |
\(\PageIndex{B}\): Measuring Glassware
Data Table \(\PageIndex{2}\)
| Objects for Practice |
Height (cm) |
SF |
Height (in) |
SF |
ratio (cm / in) |
SF |
|---|---|---|---|---|---|---|
| 250-mL Beaker | ||||||
| 250-mL Erlenmeyer flask | ||||||
| 100-mL graduated cylinder | ||||||
| Average (for ratio only) |
Once you have calculated the height ratio (cm/inches), calculate the average of the three numbers (show all work).
1. Based on your calculated average, what is the conversion factor between inches and cm?
\[1 \text{ in } = \text{ __________ cm} \nonumber\]
2. In some areas of the world where birth weight scales are absent, neonatal foot length is becoming the method of choice to diagnose preterm and low birthweight infants (less than 2500 g) responsible for 80% of neonatal deaths (Folger, Panchal, Eglovitch, Whelan, & Lee, 2020). A foot length mass data is plotted in the graph below.

In this section you will measure the length of feet for three different babies and then record in Data Table \(\PageIndex{3}\). Based on the length, use the foot length and mass graph to estimate the weight of the baby and diagnosis (preterm or term baby).
Data Table \(\PageIndex{3}\)
| Samples | Length | Weight | Diagnosis |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 |
\(\PageIndex{C}\): Measuring Volume of a Solid
Dimensions of Solid Rectangle
H = _______ cm
W = _______ cm
L = ________cm
Calculate the volume V\(_1\) using solid dimensions. Show all work.
V\(_1\) = ________
Calculate Volume of Solid Rectangle by Displacement
Initial Vol (V\(_i\)) in graduated cylinder = ______
Final Vol (V\(_f\)) in graduated cylinder = ______
Displacement volume = V\(_f\) – V\(_i\) = volume of Solid = V\(_2\) = ______
Compare V\(_1\) and V\(_2\). Were the results similar? What can you conclude about these two methods of measuring volume based on the calculated volume values?
\(\PageIndex{D}\): Measuring Mass and Volume of Water with Beaker
Mass of Beaker: _________ g
Data Table \(\PageIndex{4}\)
| Beaker |
Mass of water (g) |
Volume (mL) |
|---|---|---|
| Trial 1 | ||
| Trial 2 | ||
| Trial 3 | ||
| Mean | ||
| Std. Dev. |
\(\PageIndex{E}\): Measuring Mass and Volume of Water with Graduated Cylinder
Mass of Graduated Cylinder: _______ g
Data Table \(\PageIndex{5}\)
| Grad. Cyl. |
Mass of water (g) |
Volume (mL) |
|---|---|---|
| Trial 1 | ||
| Trial 2 | ||
| Trial 3 | ||
| Mean | ||
| Std. Dev. |
Based on the Mean and Standard Deviation Values for mass that you recorded in Data Tables \(\PageIndex{4}\) and \(\PageIndex{5}\), do you think the beaker or the graduated cylinder provides a more precise measure of volume? Explain your answer.
Post Lab Questions
The dimensions of a rectangular object were obtained as shown below. Use the data to determine the area of the rectangle. Make sure your final answer is reported to the correct number of significant figures:
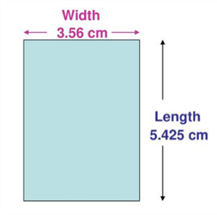
Record the length of the object correctly using each ruler:

Estimate the volume of the object to the correct number of significant figures:

You are asked to conduct an experiment where you will combine hydrochloric acid and sodium hydroxide as an acid-base neutralization reaction. You begin by placing 25.1 mL of hydrochloric acid in an empty beaker, and then add 24.46 mL of sodium hydroxide solution using a buret, to complete the experiment. What is the total volume of solution in the beaker at the end of the experiment?
Reflect on the importance of significant figures in measurements you have explored in this lab. In your summary:
a. Briefly explain how you can use significant figures to address errors in measurements.
b. Explain how you handle or account for significant figures in calculations
- i. Addition and subtraction
- ii. Multiplication and Division
c. Describe how the skills obtained in this lab can be useful for a student pursuing a career in healthcare and provide some example scenarios.

