5: Flame Tests and Atomic Spectra (Experiment)
- Page ID
- 93986
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To perform flame tests of metal cations in order to observe their characteristic colors,
- To perform calculations to determine the frequency and energy of the emitted photons.
- To relate these results to the types of electronic transitions occurring in these elements.
- To observe and understand line emission spectra of atoms using gas-discharge tubes.
- To practice writing electron configurations for these (and other) elements.
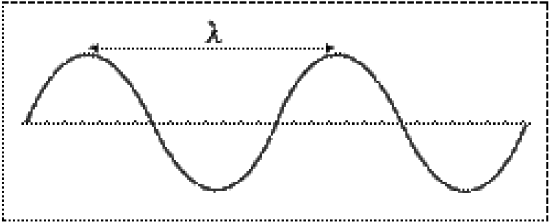
Electromagnetic radiation is energy in the form of waves. Waves are characterized by their wavelength (\(\lambda\)) and frequency (\(\nu\)). Wavelength is defined as the distance between successive crests (or troughs) on a wave, and is measured in meters. Frequency is defined as the number of waves that pass a given point every second, and is measured in 1/seconds (1/s or s-1), or Hertz (Hz).
All electromagnetic waves travel at the speed of light (\(c\)), or \(3.0 \times 10^8 m/s\). The relationship between the wavelength, frequency and speed of a wave is given by the equation:
\[c= \lambda \times \nu\]
Electromagnetic radiation also occurs as discreet “packets” called photons. The energy (\(E\)) of a photon (in Joules, J) is given by the equation:
\[E_{photon}= h \times \nu\]
Here, \(h\) is Planck’s constant, which has a value of \(6.63 \times 10^{-34} J \cdot s\).
Visible light is the most familiar example of electromagnetic radiation. Differences in the wavelengths of visible light are manifested as different colors, shown in the color spectrum below (colors can be seen in the PDF document on-line). Other examples of electromagnetic radiation include X-rays, ultraviolet light, infrared light, microwaves and radio waves.
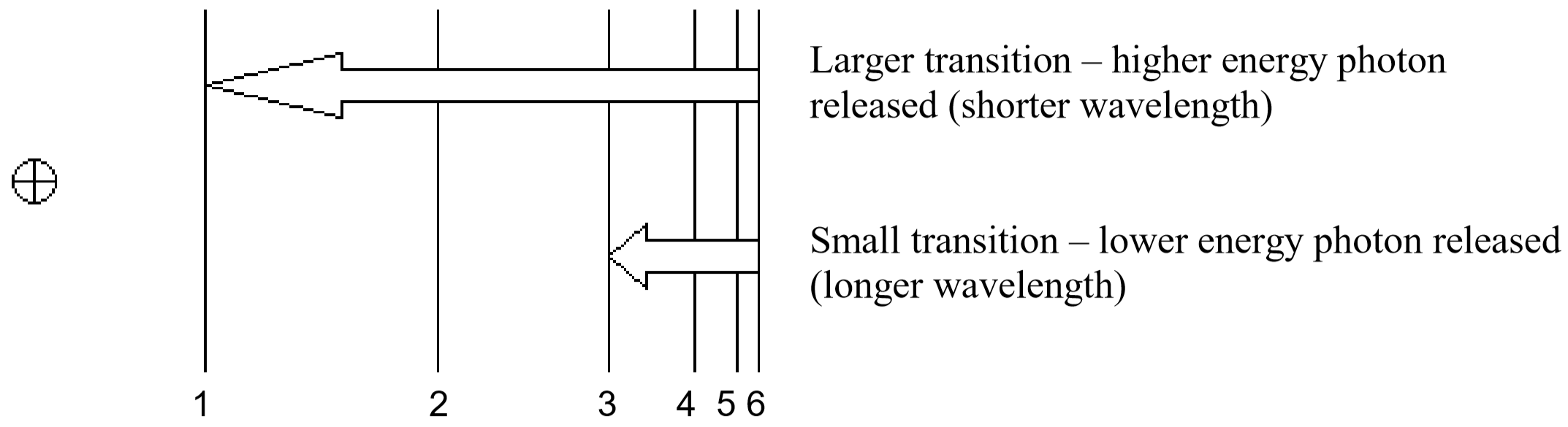
So, how does electromagnetic radiation relate to flame tests? Well, when an atom or ion absorbs energy, its electrons can make transitions from lower energy levels to higher energy levels. The energy absorbed could be in the form of heat (as in flame tests), or electrical energy, or electromagnetic radiation. However, when electrons subsequently return from higher energy levels to lower energy levels, energy is released predominantly in the form of electromagnetic radiation.
The spacing between energy levels in an atom determines the sizes of the transitions that occur, and thus the energy and wavelengths of the collection of photons emitted.
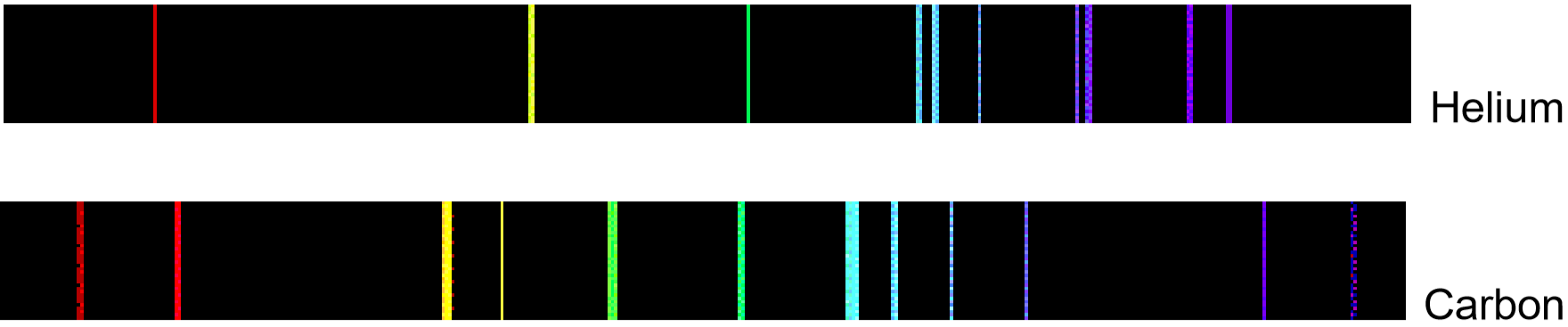
If emitted photons are in the visible region of the spectrum, they may be perceived as lines of different colors (note that photons outside the visible spectrum may also be emitted, but cannot be seen). The result is called a line emission spectrum, and can serve as a ‘fingerprint’ of the element to which the atoms belong. For example, the line spectra shown below for the elements helium and carbon are clearly quite different (colors can be seen in the PDF document on-line).
Unfortunately, techniques more sophisticated than those used in this lab are required to obtain such line spectra. To the naked eye, when an element is vaporized in a flame (or an electrical discharge)the emission spectrum will appear to be just one color. For example, helium gas when excited by an electrical discharge emits light that appears an orange- peach color. This one color results from a combination of all lines of the emission spectrum, in proportion to their intensities. As many elements will still produce distinctive colors under such conditions, simple flame tests can be used to identify these elements. In fact, flame tests were used to identify elements long before the invention of modern techniques, such as emission spectroscopy.
Procedure
Materials and Equipment
Looped platinum or nichrome wires, wash bottle with distilled water, Bunsen burner, and the following solutions: \(\ce{LiCl}\) (aq), \(\ce{NaCl}\) (aq), \(\ce{KCl}\) (aq), \(\ce{CuCl2}\) (aq), \(\ce{BaCl2}\) (aq), \(\ce{CaCl2}\) (aq). Gas discharge tubes for hydrogen, helium, mercury, neon, argon, krypton, and diffraction grating
Exercise appropriate caution when using the Bunsen burner.
Experimental Procedure - This will be performed as an instructor demonstration only.
Part A: Flame Tests of Metal Cations
Your instructor will dip a looped wire into one of the solutions supplied, and then hold it in the Bunsen burner flame. Students will record the dominant flame color observed.
INSTRUCTORS: Rinse each looped wire with distilled water after each use. Place the rinsed looped wire into the empty test tube provided.
Analysis: For each metal cation flame test performed, determine the wavelength corresponding to the observed flame color from the table below.
*Wavelength values here are given for the mid- range of the color indicated.
|
Dominant Color |
Approximate Wavelength (in nm)* |
|---|---|
|
Red |
701 |
|
Red-Orange |
622 |
|
Orange |
609 |
|
Orange-Yellow |
597 |
|
Yellow |
587 |
|
Yellow-Green |
577 |
|
Green |
535 |
|
Green-Blue |
492 |
|
Blue |
474 |
|
Blue-Violet |
455 |
|
Violet |
423 |
Part B: Line Emission Spectra
- Gas-discharge tubes for hydrogen, helium and mercury are set up at the front bench. Go to any available station and use the hand-held spectroscope.
- Align the slit on the wider end so that you can see the light through the view window on the opposite end. It should appear as a clear, vertical line, and result in several colored lines appearing in the view. You should also be able to see the nm markings (make sure it is not upside-down) below the colored lines in the view.
- Record the spectral lines, indicating colors in their specific locations.
Lab Report: Flame Tests and Atomic Spectra
Part A: Flame Tests of Metal Cations Experimental Data and Observations
|
Solution |
Dominant Flame Color |
Wavelength (nm) |
Flame Intensity (low, medium, high) |
Flame Duration (seconds) |
|---|---|---|---|---|
|
\(\ce{BaCl2}\) |
||||
|
\(\ce{CaCl2}\) |
||||
|
\(\ce{CuCl2}\) |
||||
|
\(\ce{KCl}\) |
||||
|
\(\ce{LiCl}\) |
||||
|
\(\ce{NaCl}\) |
Part B: Line Emission Spectra
Experimental Data and Observations
- Draw the spectral lines for the indicated elements. Indicate names colors below each line drawn.
Line Emission Spectrum for Helium
- colors:
- nm:
Line Emission Spectrum for Mercury
- colors:
- nm:
Line Emission Spectrum for Hydrogen
- colors:
- nm:
Data Analysis
Using the wavelengths recorded above, calculate the corresponding wavelengths, frequencies and photon energies for each compound tested. Record the values, in scientific notation, in the table below.
|
Solution |
Wavelength (m) |
Frequency (s-1) |
Energy (J) |
|---|---|---|---|
|
\(\ce{BaCl2}\) |
|||
|
\(\ce{CaCl2}\) |
|||
|
\(\ce{CuCl2}\) |
|||
|
\(\ce{KCl}\) |
|||
|
\(\ce{LiCl}\) |
|||
|
\(\ce{NaCl}\) |
Show a set of sample calculations for \(\ce{NaCl}\) only below. Clearly show any equations you have used.
- Wavelength (in m):
- Frequency (in s-1):
- Energy (in J):
Questions
- Complete the following paragraph by circling the correct responses:
In this experiment, the metal cations in the solutions were initially in the (ground, excited) state. When placed in the flame, the metals then (absorbed, emitted) energy as (electricity, heat, EM radiation). When this occurred, electrons made transitions from (low, high) energy levels to (low, high) energy levels. The metals were then in the (ground, excited) state. The electrons in these metals then made transitions from (low, high) energy levels to (low, high) energy levels, resulting in the (absorption, emission) of energy as (electricity, heat, EM radiation).
- What evidence is there that the colors observed in the flame tests are due to the metals, and not the nonmetals in the compounds tested?
- Which metal cation was observed to emit radiation with the longest wavelength?
Compared to the other metals studied, did the radiation emitted by this metal cation have
• the highest or lowest frequency?
• the highest or lowest energy?
- Why do the gas-discharge tubes need to be turned “on” before a color can be seen?
- You observed the spectral lines for different elements. What is happening within an atom that causes it to emit light in specific lines in a spectrum?
- Why did the different elements have different line emission spectra?
- The radio station JACK FM broadcasts at a frequency of 93.5 kHz. Calculate its wavelength (\(\lamda\)) in nanometers. (Hz = 1/s)
- For the same radio station, calculate the energy (E) in kilojoules, kJ.