11: Solubility and Borax (Experiment)
- Page ID
- 94010
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To learn about the solubility and solubility equilibria.
- To see how equilibrium constants change with temperature.
- To determine the values of \(\Delta H^o\), \(\Delta S^o\), and \(\Delta G^o\) for a reaction.
Have you ever wondered how certain mineral deposits form in the ground? Or why you can dissolve more sugar in hot water than in cold? It turns out these processes are related by a concept known as the chemical solubility-product equilibrium constant, or \(K_{sp}\).
Let’s consider a very familiar example of solubility. When table sugar, \(\ce{C12H22O11(s)}\), is added to water it dissolves until the solution becomes saturated. At this point the water contains as much sugar as it can hold and any additional sugar added falls to the bottom of the glass. If we write the chemical equation for the dissolution of sugar in water as,
\[\ce{C12H22O11(s) <=>[+ H_2O] C12H22O11(aq)} \label{1}\]
then the amount of sugar that can be dissolved at a particular temperature is given by the equilibrium constant expression,
\[ K_{sp} = [\ce{C12H22O11}] \label{2}\]
Here \([\ce{C12H22O11}]\) is the molar concentration of the dissolved sugar, and the subscript sp on the equilibrium constant stands for solubility product. The value of \(K_{sp}\) for a particular compound can be used to determine how much of that compound can be dissolved in solution. Notice that we do not include the concentration of the solid reactant in the \(K_{sp}\) expression because the concentration of a pure solid is essentially constant, and so we set it equal to unity.
What would happen to our saturated sugar solution if we were to evaporated off some of the water? In this case the concentration of the dissolved sugar, \(\ce{[C12H22O11]}\), would increase. However, because the solution is already saturated, this means that the concentration of dissolved sugar would now exceed the value of \(K_{sp}\) (or that \(Q_{sp} > K_{sp}\)). To return the system to equilibrium some of the dissolved sugar must precipitate out of the solution. Notice that this shift of the equilibrium position of Equation \ref{1} to the left in response to the increase in \(\ce{C12H22O11(aq)}\) concentration is also in accordance with Le Chatelier’s principle.
Mineral deposits such as sulfur, borax, and calcium carbonate (limestone) found around lakes beds form in a similar way. If due to drought, the diversion of water sources, or other reasons the influx of water to a lake diminishes, then the water level in the lake will begin to drop. This results in an increase in the concentration of dissolved solids in the lake water. As the concentration of dissolved minerals pass their solubility product equilibrium values, they begin to precipitate out. This typically results in the formation of bands of mineral deposits around the lake. If you travel through Death Valley and parts of the southwest United States you can see, "dry lakes," where colorful rings of mineral deposits such as sulfur and borax surround once-filled lake beds.
For ionic species the value of \(K_{sp}\) depends of the concentration of each of the ions present in solution. Consider the dissolution reaction of magnesium hydroxide, \(\ce{Mg(OH)2}\) (s), described by,
\[\ce{ Mg(OH)2 (s) <=> Mg^{2+} (aq) + 2 OH^{-} (aq)} \label{3}\]
where \(s\) is the solubility of \(\ce{ Mg(OH)2}\) (s) in moles per liter and \(2s\) is the solubility of \(\ce{OH^{-}}\) (aq).
The solubility product expression depends on the concentrations of both the \(\ce{Mg^{2+}}\) (aq) and the \(\ce{OH^{-}}\) (aq) ions formed and is given by:
\[K_{sp}= [\ce{Mg^{2+}}][\ce{OH^{-}}]^{2} = (s)(2s)^{2} = 4s^{3} \label{4}\]
To determine the value of \(K_{sp}\) for a saturated \(\ce{Mg(OH)2}\) solution, you can titrate an aliquot of the solution using a strong acid to measure the concentration of \(ce{OH^{-}}\) (aq). You can then determine the value of \(s\) from the relationship \(2s = [\ce{OH^{-}}]\) in Equation \ref{3}. Finally, you can substitute this value into Equation \ref{4} to obtain the value of \(K_{sp}\) for magnesium hydroxide at the observed temperature. Thus, one method of determining the value of \(K_{sp}\) is to titrate one of the species present in solution at equilibrium. In this experiment you will use a similar method to measure the value of \(K_{sp}\) at various temperatures for the dissolution of borax.
Borax is a boron-containing mineral that occurs in nature as a white powder composed of soft highly soluble crystals. Borax was first discovered by silk-road travelers in dry lake beds in Tibet and later found in the California and Nevada deserts of America. It is the active ingredient in some soaps and detergents, a flux used in soldering, an anti-fungal agent, and is even used as a texturizer in some prepared foods. It is also used in the manufacture of the thermoresistant borosilicate glass commonly marketed as, "Pyrex." You may be most familiar with borax because of the laundry additive brand, “20 Mule Team Borax.”
The empirical formula of the natural form of the mineral borax is \(\ce{Na2B4O7*10H2O}\) and its IUPAC name is sodium tetraborate decahydrate, but here we shall simply refer to it by its common name, “borax.” The structure of the tetraborate anion, \(\ce{B4O5(OH)4^{2-}}\), is shown in Figure 1. From this figure you can see that a more structurally accurate description of the borax molecule is given by the chemical formula, \(\ce{Na2B4O5(OH)4*8H2O}\), which is the one we shall use here.
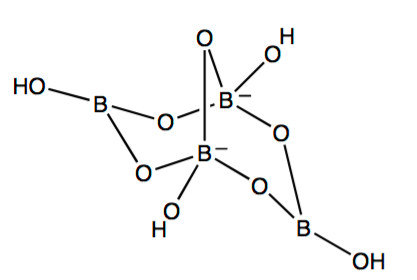
Figure 1: The Tetraborate Anion, \(\ce{B4O5(OH)4^{2-}}\)
The chemical equation for the dissolution of borax may be written as:
\[\underbrace{\ce{Na2[B4O5(OH)4]*8H2O (s)}}_{\text{Borax}} \ce{ <=> 2 Na^{+} (aq) + } \underbrace{\ce{B4O5(OH)4^{2-} (aq)}}_{\text{Tetraborate Anion}} \ce{+ 8 H2O(l) } \label{5}\]
The tetraborate anion formed in solution is a weak base and reacts with water according to:
\[\ce{B4O5(OH)4^{2-} (aq) + 5 H2O(aq) <=> 4 H3BO3 (aq)+2 OH^{-}(aq)} \label{6}\]
The products of the reaction are boric acid, \(\ce{H3BO3}\) (aq), a weak acid, and the hydroxide ion, \(\ce{OH^{-}}\) (aq), a strong base.
We can determine the concentration of the tetraborate anion in solution (and thus the amount of dissolved borax) in the following way: First, we collect a sample of the saturated solution at equilibrium, being careful only to collect the liquid portion and not any of the solid borax in equilibrium with it. Next we titrate the hydroxide ions using a strong acid, say \(\ce{HCl}\) (aq). As the hydroxide ions are removed from solution by the acid, more tetraborate anions are converted into boric acid and hydroxide ions, in accordance with Le Chatelier’s principle. That is, as \(\ce{OH^{-}}\) ions are removed from solution by the strong acid, the reaction described by Equation \ref{6} will shift right. We can represent the overall reaction between the tetraborate anions and the hydronium ions formed from the strong acid, \(\ce{H3O^{+}}\) (aq), that occurs during the titration as:
\[\ce{B4O5(OH)4^{2-} (aq) + 2 H3O^{+}(aq)+H2O (l) <=> 4 H3BO3 (aq)} \label{7}\]
The reaction described by Equation \ref{7} will continue until we reach the equivalence point of the titration. At this point all of the tetraborate anions have been converted to boric acid and all of the \(\ce{OH^{-}}\) ions in the solution have been neutralized. Because all of the base has been neutralized the addition of more strong acid causes the pH of the solution to shifts sharply from basic to acidic. The presence of an acid-base indicator allows us to observe this shift and will serve to signal the endpoint of our titration. The indicator we will use for this titration is bromocresol green, which changes color from blue to yellow at a pH of 4.8 upon the addition of acid.
From the amount of acid required to reach the equivalence point, we can determine the concentration of tetraborate anion present in the sample of our saturated borax solution. From this concentration we can determine the value of \(K_{sp}\) for borax using a method analogous to that described previously for the dissolution of \(\ce{Mg(OH)2}\) (s). This is the method you will use in this experiment to determine the value of \(K_{sp}\) for borax.
In this experiment you will also observe how the solubility of borax varies with temperature. You know, for example, that sugar dissolves more readily and to a greater extent in warm water than in cold. You may also be aware that other substances dissolve less readily in hot water than in cold. For example, calcium carbonate, \(\ce{CaCO3}\) (s), a major component of boiler scale is less soluble in warm water than in cold, and so tends to precipitate out as a white crust on the walls of hot-water heaters, cookware, and teakettles. In this experiment you will study the dependence of \(K_{sp}\) for borax on temperature. You will then use your \(K_{sp}\) and temperature data to determine the values of \( \Delta H^{o}_{rxn}\), \( \Delta S^{o}_{rxn}\), and \( \Delta G^{o}_{rxn}\) for the dissolution reaction described by Equation \ref{5}.
We can equate the thermodynamic expressions:
\[\Delta G^{o}_{rxn}=\Delta H^{o}_{rxn}-T \Delta S^{o}_{rxn} \label{8}\]
and
\[\Delta G^{o}_{rxn}=-RT \ln K \label{9}\]
to obtain,
\[\ln K=-\frac{\Delta H^{o}_{rxn}}{R} \left(\dfrac{1}{T}\right) + \frac{\Delta S^{o}_{rxn}}{R} \label{10}\]
Equation \ref{10} is one form of the van 't Hoff equation that describes the temperature dependence of the thermodynamic equilibrium constant, \(K\), on temperature. The value of the thermodynamic equilibrium constant, \(K\), can be related to \(K_{sp}\) by,
\[K = \frac{K_{sp}}{Q^{o}_{sp}} \label{11}\]
where \(Q^{o}_{sp}\) is the standard reaction solubility product quotient, which has a numerical value of unity and units that are the same as those as \(K_{sp}\). Thus, \(K\) in this experiment is the numeric but unitless value of \(K_{sp}\).
Notice that Equation \ref{10} is linear and of the form \(y=mx+b\), where \(y= \ln K\), \(m=\Delta H^{o}_{rxn}/R\), \(x = 1/T\), and \(b = \Delta S^{o}_{rxn}/R\). Therefore, a plot of \( \ln K\) versus \(1/T\) should yield a straight from which the values of \( \Delta H^{o}_{rxn}\) and \( \Delta S^{o}_{rxn}\) for the reaction described by Equation \ref{5} can be obtained. We can then use Equation \ref{8} to determine the value of \( \Delta G^{o}_{rxn}\) for the reaction at 25°C.
These calculations assume that the dissolution reaction described by Equation \ref{5} is the only one occurring in solution. In fact, the actual dissolution process for most substances is almost always more involved than that idealized by their \(K_{sp}\) equilibrium expression. Nevertheless, from the data we obtain we will be able to make a wide variety of predictions about the solubility of borax and will gain a better understanding of the chemistry of dry lakes and the dissolution of minerals and other chemicals in solution.
Procedure
Materials and Equipment
You will need the following additional items for this experiment: three 50-mL burets and buret stands 5.00-mL pipet, pipet bulb, bucket of ice, 0.5-M standardized \(\ce{HCl}\) solution (should be in the laboratory room), fine-tipped permanent black marker (one can be shared by the entire lab room)
Students must wear safety goggles at all times. Use caution when working with the 0.5 M hydrochloric acid solution; be sure to rinse any area of skin that comes into contact with this solution well.
WASTE DISPOSAL: All solutions used in this lab must be disposed of in the proper chemical waste container.
CLEAN-UP: Borax crystals are difficult to remove from glassware and the bench tops once dry. Be certain to rinse all glassware that comes into contact with the borax thoroughly using warm water at the end of the experiment. Also be certain to wipe down any spills of the borax solution that occur using several rinses of warm water. Your lab instructor may chose to deduct points from any group leaving a “white crust” behind on their bench top!
Experimental Set-up and Procedure:
This experiment requires teams of at least 3 students
Note on Cleaning Glassware: Do NOT use soap to wash glassware for this experiment or you will be titrating the soap residue as well as the borax (soap is also a base). You should rinse all glassware several times with deionized water before beginning this experiment. You should clean and rinse three 250-mL Erlenmeyer flasks, an 800-mL beaker, two 400-mL beakers, a 150-mL beaker, a small test tube, two thermometers, a glass stirring-rod, the three 50-mL burets, and the 5.00-mL pipet before beginning.
A Note about the Order of Trials for this Experiment: It is critical that the trials in this experiment be performed in order from cold to hot, and not the reverse. This is because borax solutions tend to supersaturate on cooling, and so running the experiment from hot to cold may result in significant errors in your results.
Trial 1, 10°C:
- Rinse an 800-mL beaker with deionized water and then with about 5-mL of the 0.5 M standardized \(\ce{HCl}\) solution. Fill this beaker with about 500 mL of the standardized \(\ce{HCl}\) solution. Record the exact concentration of the standardized 0.5 M \(\ce{HCl}\) solution (as given on the reagent label) on your data sheet. Label this beaker, “standardized HCl.” You will use this as your standardized \(\ce{HCl}\) solution throughout the experiment. Should you require additional standardized \(\ce{HCl}\) solution, be sure to check that the concentration is the same as the one in your beaker. If it is different you will need to rinse and refill your buret with this new solution and repeat any titrations underway making note of the new concentration for your calculations.
- Rinse your three 50-mL burets using about 5-mL of the 0.5 M standardized \(\ce{HCl}\) solution from your beaker and then fill each buret with this solution. Be certain that there are no small air bubbles in the buret tips and that the tips are pressed in firmly and do not leak. Clamp each buret to a separate buret stand, making sure that they are vertical.
- Using the 5.00-mL pipet dispense exactly 5.00 mL of deionized water into a clean dry small test tube. The water should come to about halfway up the test tube. Using a permanent marker, mark this test tube exactly at the water line. Do this carefully as this tube will become your measuring standard for the entire lab! Now empty the calibrated small test tube and set it aside.
- Weigh approximately 10 grams of solid borax and place it into a 150-mL beaker. Fill this beaker to about the 75-mL mark with deionized water. The mass and volume used here need only be approximate.
- Using your glass stirring-rod, stir the borax solution you have made and place it into an ice- water bath. Insert your thermometer into the solution. Continue to stir the solution gently every minute or so as it cools. Allow the solution to cool to about 10°C.
- It is important that the borax solution be saturated in order to achieve equilibrium between the solid and dissolved phases. If you can see solid borax crystals at the bottom of the beaker you are at equilibrium; if not you should add some additional solid borax until you can see white crystals at the bottom of the solution. Later as you heat the solution you may need to add additional solid borax to achieve this condition.
- While your solution is cooling, set up a heating apparatus using a ring stand, a wire mesh, and a Bunsen burner. Light the burner and set a half-filled 400-mL beaker of deionized water on the apparatus. Label this beaker “hot water rinse.” Keep the temperature of this water between about 60°C to 80°C. You will need this hot deionized water throughout the experiment. Add more deionized water to this beaker as needed.
- When the saturated borax solution in the 150-mL beaker reaches about 10°C, stop stirring the solution and allow the borax crystals in the solution to settle. This takes about 2 minutes. After the solid has settled record the exact temperature of the solution to the nearest tenth of a degree on your data sheet.
- Grip the calibrated small test tube with the 5.0-mL mark that you prepared earlier with your wire test-tube holder. Carefully measure out exactly 5.0 mL of the 10°C saturated borax solution using the calibrated small test tube. Be certain to pour only the clear liquid from the top of the solution into your small test tube and not any of the solid crystals from the bottom. Quickly pour this solution from the calibrated small test tube into a clean rinsed 250-mL Erlenmeyer flask. Label this flask, “Sample 1.”
- Using your beaker tongs to grasp the hot beaker of deionized water, fill the calibrated small test tube to the brim with hot deionized water to dissolve any borax crystals that formed on the inside the tube and pour this into the 250-mL Erlenmeyer flask labeled “Sample 1.” Repeat this rinse once more to be certain that all the borax from the calibrated small test tube has been transferred to the 250-mL Erlenmeyer flask.
- Next measure out a second 5.0-mL sample of the 10°C saturated borax solution (checking that the temperature is still the same) using the calibrated small test tube and pour this into a second clean rinsed 250-mL Erlenmeyer flask. Label this flask, “Sample 2.” Again fill the small test tube to the brim with deionized water from the hot water bath twice to rinse the small test tube. Pour these two rinses into this 250-mL Erlenmeyer flask as well.
- Repeat this procedure with the third 250-mL Erlenmeyer flask, labeling it, “Sample 3,” so that you now have three 250-mL Erlenmeyer flasks, each containing a 5.0-mL sample of the 10°C saturated borax solution and some warm deionized water.
- Bring the volume of water in each of the three 250-mL Erlenmeyer flasks up to about the 50-mL mark by adding room temperature deionized water. These amounts do not need to be exact because adding more or less deionized water will not change the number of borax molecules in each flask.
- Add four drops of bromocresol green indicator to each of the three 250-mL Erlenmeyer flasks. The solutions in each should turn a light blue color. You are now ready to begin the first titration.
- Working as a team you should now titrate the contents of each of the three 250-mL Erlenmeyer flasks. Because of the number of titrations required for this experiment, you should perform this step in parallel with three team members simultaneously performing the three titrations. The titration endpoint occurs when one drop of the standardized acid changes the color of the solution from light blue to yellow. Be certain to record both the initial and final volumes of 0.5 M standardized \(\ce{HCl}\) solution required for each titration to the correct number of significant figures on your data sheet. It is suggested that you double- check all buret readings with other members of your team to be sure they are accurate.
- Rinse out the three 250-mL Erlenmeyer flasks with deionized water and refill the three burets with your 0.5 M standardized \(\ce{HCl}\) solution.
Trial 2, 30°C:
- Prepare a second hot-water bath using another 400-mL beaker and another burner. This will not be used for a rinse, so you may use tap water to fill this second bath. Place the 150- mL beaker containing the borax solution into this hot-water. You may need to clamp the 150-mL beaker in place to keep it from turning over in the bath. Allow the borax solution in the 150-mL beaker to warm to about 30°C. (Do not use the hot deionized water bath for this or you may contaminate the deionized rinse water with borax from the outside of the 150- mL beaker). Be certain there are still visible crystals at the bottom of the 150-mL beaker so that you know the borax solution is in equilibrium with the solid phase and thus still saturated. If necessary, add more solid borax to the solution so that white crystals are visible at the bottom of the beaker at all times.
- Be careful not to overheat the borax solution. If you allow the borax to heat past the desired temperature and then cool back down, you may get supersaturation of the borax. This could result in significant errors in your experimental results. Should you overheat the solution, either collect your data at higher temperatures, or discard the borax solution in the proper waste container and prepare a fresh one, being careful not to exceed the temperature desired the second time. (The later trials for this experiment do not need to be at exactly 30°C, 50°C, and 70°C, so long as they are somewhere around these values).
- When the saturated borax solution reaches about 30°C, stop stirring the solution and allow the borax crystals in the solution to settle as before. Then record the exact temperature of the solution to the nearest tenth of a degree on your data sheet.
- Using your calibrated small test tube, carefully measure out three 5.0-mL samples of the approximately 30°C borax solution into each of the three clean rinsed 250-mL Erlenmeyer flasks rinsing the calibrated small test tube twice with the hot deionized water following each measurement as before. Remember to collect these rinses in the corresponding Erlenmeyer flask as well. Once again be certain no solid borax from the bottom of the 150-mL beaker is transferred to the calibrated small test tube during this process.
- Again bring the volumes in each of the three 250-mL Erlenmeyer flasks to 50 mL using room temperature deionized water. Add four drops of bromocresol green indicator to each solution and titrate each as before. Record all your results on your data sheet.
- At the end of this step rinse out the three 250-mL Erlenmeyer flasks with deionized water and refill the three burets with your 0.5 M standardized \(\ce{HCl}\) solution.
Trials 3 and 4; 50°C and 70°C:
- Using the hot water bath, heat the borax solution to about 50°C for Trial 3 and then to 70°C for Trial 4, collecting three 5.0-mL samples and performing three indicator titrations at each temperature as before.
- You may need to add additional borax to the solution in the 150-mL beaker as you heat it to maintain equilibrium. Be certain that for each trial you can see crystals of solid borax at the bottom of the solution in the 150-mL beaker. Also be sure to allow the solution to settle for at least 2 minutes before collecting your 5.0-mL samples. Again, be careful not to overheat the borax solution between trials.
Clean-up
Dispose of all solutions in the proper chemical waste container. Wet a paper towel with some of the hot deionized water and use this to wipe down your bench top. You can also use this water to help rinse any borax out of your glassware. Be sure all these rinses end up in the proper waste container as well.
Return the equipment you borrowed to its proper location in the laboratory room or to the chemistry stockroom. Finally, be certain that there is no white film of borax remaining on your bench top before leaving the room.
Lab Report: Minerals, Dry Lakes, and Borax
Name: ____________________________ Lab Partner: ________________________
Date: ________________________ Lab Section: __________________
Experimental Data
Molarity of standardized 0.5 M \(\ce{HCl}\) solution (from label on bottle): __________________
10°C Titration Data: Measured Temperature (°C): _________________
|
Sample 1 |
Sample 2 |
Sample 3 |
|
|---|---|---|---|
|
Initial Buret Volume |
|||
|
Final Buret Volume |
|||
|
Volume of \(\ce{HCl}\) added |
|||
|
Millimoles of \(\ce{HCl}\) added |
|||
|
Millimoles of \(\ce{B4O5(OH)4^{2-}}\) ions |
|||
|
Volume of \(\ce{B4O5(OH)4^{2-}}\) sample |
5.0 mL |
5.0 mL |
5.0 mL |
|
\([\ce{B4O5(OH)4^{2-}}]\) |
- Average \([\ce{B4O5(OH)4^{2-}}]\): __________________
- Measured Temperature (K): __________________
- Show a sample calculation below for each of the calculated entries in your table for Sample 1: Do not forget to consider the stoichiometery of the acid-base titration reaction in your calculations; it is not 1:1.
Record your data and calculations for your other temperature trials in the three tables below. There is no need to show calculations for the entries in these three tables.
30°C Titration Data: Measured Temperature (°C): __________________
|
Sample 1 |
Sample 2 |
Sample 3 |
|
|---|---|---|---|
|
Initial Buret Volume |
|||
|
Final Buret Volume |
|||
|
Volume of \(\ce{HCl}\) added |
|||
|
Millimoles of \(\ce{HCl}\) added |
|||
|
Millimoles of \(\ce{B4O5(OH)4^{2-}}\) ions |
|||
|
Volume of \(\ce{B4O5(OH)4^{2-}}\) sample |
5.0 mL |
5.0 mL |
5.0 mL |
|
\([\ce{B4O5(OH)4^{2-}}]\) |
- Average \([\ce{B4O5(OH)4^{2-}}]\): _________________
- Measured Temperature (K): __________________
50°C Titration Data: Measured Temperature (°C): __________________
|
Sample 1 |
Sample 2 |
Sample 3 |
|
|---|---|---|---|
|
Initial Buret Volume |
|||
|
Final Buret Volume |
|||
|
Volume of \(\ce{HCl}\) added |
|||
|
Millimoles of \(\ce{HCl}\) added |
|||
|
Millimoles of \(\ce{B4O5(OH)4^{2-}}\) ions |
|||
|
Volume of \(\ce{B4O5(OH)4^{2-}}\) sample |
5.0 mL |
5.0 mL |
5.0 mL |
| \([\ce{B4O5(OH)4^{2-}}]\) |
- Average \([\ce{B4O5(OH)4^{2-}}]\):_________________
- Measured Temperature (K): __________________
70°C Titration Data: Measured Temperature (°C): __________________
|
Sample 1 |
Sample 2 |
Sample 3 |
|
|---|---|---|---|
|
Initial Buret Volume |
|||
|
Final Buret Volume |
|||
|
Volume of \(\ce{HCl}\) added |
|||
|
Millimoles of \(\ce{HCl}\) added |
|||
|
Millimoles of \(\ce{B4O5(OH)4^{2-}}\) ions |
|||
|
Volume of \(\ce{B4O5(OH)4^{2-}}\) sample |
5.0 mL |
5.0 mL |
5.0 mL |
| \([\ce{B4O5(OH)4^{2-}}]\) |
- Average \([\ce{B4O5(OH)4^{2-}}]\): _________________
- Measured Temperature (K): __________________
Data Analysis
Complete the data summary table below:
|
Trial |
Average \([\ce{B4O5(OH)4^{2-}}]\) |
Calculated borax \(K_{sp}\) |
\(\ln K\) |
Measured temperature (K) |
\(1/T\) (K–1) |
|---|---|---|---|---|---|
|
10°C |
|||||
|
30°C |
|||||
|
50°C |
|||||
|
70°C |
- Show a sample calculation below illustrating how you obtained the value of \(K_{sp}\) for the 10°C trail. Do not forget to consider the reaction stoichiometery given by Equation \ref{5}.
Use Excel to create a graph of \(\ln K\) versus \(1/T\) for your data. Your graph should have an appropriate title and labeled axes with an appropriate scale. Using the Excel trendline function, add a best-fit line to your plotted data and have Excel display the equation of this line and its R2 value on your graph. Submit this graph with your report.
- Use this graph to determine the values of \(\Delta H^{o}_{rxn}\) and \(\Delta S^{o}_{rxn}\) for the reaction described by Equation \ref{5}. Be certain to include the proper units for each! Show your calculations:
- \(\Delta H^{o}_{rxn}\) (and units):________________________
- \(\Delta S^{o}_{rxn}\) (and units):________________________
- Use the values of \(\Delta H^{o}_{rxn}\) and \(\Delta S^{o}_{rxn}\) you obtained to determine the value of \(\Delta G^{o}_{rxn}\) 25°C for the reaction described by Equation \ref{5}. Show your calculations below:
- \(\Delta G^{o}_{rxn}\) (and units):________________________
Questions
- Does the solubility of borax increase or decrease with increasing temperature? Use both your physical observations and your \(K_{sp}\) measurements to justify your response.
- Does your value of \(\Delta H^{o}_{rxn}\) suggest that the reaction for the dissolution of borax described by Equation \ref{5} is exothermic or endothermic? Explain why this result is consistent with your answer to Question 1 above.
- The value of \(\Delta G^{o}_{rxn}\) that you determined for the dissolution of borax at 25°C should be positive (if not you should check your work).Given that \(\Delta G^{o}_{rxn} > 0\),how do you explain that some of the borax actually dissolved at 25°C?
- A geologist removes a sample of water from a lake in Nevada where the water level has been slowly dropping over time. The sample is found to be 0.02 M in borax. The lake is circular in shape and is currently 500 meters in diameter and 50 meters deep. Use your experimental data to predict the level of the lake when borax will begin to precipitate on the shore if the mean temperature of the lake water is 15°C. Assume that the lake is equally deep at all points.


