Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

Sugar Solution Density

Last updated

Mar 13, 2023
Save as PDF
- Stereoisomerism and Smell
- The Amazing Water Diet

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Sugar solutions or "syrups" are used extensively in canning, and sometimes referred to as "heavy" or "light" syrups.

The terms heavy and light are commonly used in two different ways. We refer to weight when we say that an adult is heavier than a child. On the other hand, something else is alluded to when we say that one syrup is heavier than another. A teaspoon of heavy syrup would obviously weigh less than a gallon of light syrup, but heavy syrup is heavier in the sense that a given volume weighs more than the same volume of light syrup. It's interesting that a given volume of "heavy cream" actually weighs less than "light cream" (in this case, "heavy" refers to the thickness, or percent milk fat).

In "Molecular Gastronomy", Herve This (pronounced Thees) points out^[2] that more precision is needed in canning recipes. Some call a heavy syrup 1 cup sugar to 2 cups water (a ratio of 0.5:1) while others refer to a medium syrup as 3-1/4 c sugar to 5 c water (a ratio of 0.65:1). The latter is actually heavier, or denser. Which is better for canning?

Poster with two women standing behind a table of food. The text on the poster says Waste not-Want not, prepare for winter. Save perishable foods by preserving now.

WW I Canning Poster

Density

What we are actually comparing is the mass per unit volume, that is, the density. In order to determine these densities, we might weigh a cubic centimeter of each syrup. If the heavy syrup weighed 1.30 g and the light 1.15 g, we could describe the density of heavy syrup as 1.30 g cm^–3 and that of light syrup as 1.15 g cm^–3. (Note that the negative exponent in the units cubic centimeters indicates a reciprocal. Thus 1 cm^–3 = 1/cm³ units for our densities could be written as g/cm³, or g cm^–3. In each case the units are read as grams per cubic centimeter, the per indicating division.) We often abbreviate "cm³" as "cc", and 1 cm³ = 1 mL exactly by definition.

In general it is not necessary to weigh exactly 1 cm³ of a material in order to determine its density. We simply measure mass and volume and divide volume into mass:

$\text{Density} = \dfrac{\text{mass}} {\text{volume}}$

$\rho = \dfrac{\text{m}} {\text{V}}$

where ρ = density m = mass V = volume

Canning Fruit

The graph below shows that the density of a syrup or beverage can be used to determine its percent sugar. This is done routinely in the beer and fruit juice industry, but the dependence of density on sugar concentration is the basis of a rational method of choosing the right syrup composition for canning:

This notes that in heavier syrups, fruit floats, and is dehydrated by osmosis, shrivelling them up. In light syrups, fruits sink and break apart, absorbing water by osmosis. He recommends making the syrup a little too heavy, then adding the fruit, and adding water until the fruit just ceases to float.

Plot of Density vs. Sucrose Concentration

Example $\PageIndex{1}$ : Densities of Foods

Calculate the density of (a) a piece of peach whose mass is 37.42 g and which, when submerged in water, increases the water level in a graduated cylinder by 35.80 ml; (b) a "heavy syrup" made by dissolving 4.00 cups (200 g/cup) of sugar in 5.0 cups (236.6 mL/cup) to make 7.00 cups of syrup. A cup of water has a volume of 8 fluid ounces, and weighs 8 oz or about 226 g. Will the peach float?

Solution

a) Since the submerged peach displaces its own volume,

$\text{Density} =\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{37.42 g} {35.80 mL} = \text {1.045 g/mL or 1.045 g mL}^{-1}$

b) The volume of the syrup must be calculated first, using the formula

$\text{V} = \text{7.00 cups} \times \text{240} \dfrac{\text{mL}}{\text{cup}} = \text{1680} \text{mL} \text{ or } \text{1.68 x 10}^3 \text{mL}$

The mass of sugar is 4.00 cups x 200 g/cup = 800 g, and the mass of water is 5.00 cups x 226 g/cup = 1130 g or 1.13 x 10³ g.

So the total mass is 800 g + 1130 g = 1930 g or 1.93 x 10³ g.

Then $\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{1930 g} {1680 cm^{3}}$

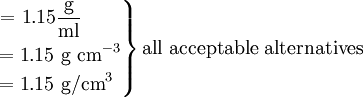
The fruit has a density of 1.045 g/ml, while the syrup has a density of 1.15 g/ml, so the fruit will float, being less dense.

If you remember that the density of water is very close to 1.0 g/ml or 1.0 oz/fluid ounce ("a pint's (16 oz) a pound (16 oz) the world around"), you may notice that if a cup is 236.6 ml, as given, it should weigh 236.6 g, not the 226 g given above. This is due to the imprecision in the definition of a "cup". There is a US customary cup, 236.7 mL, or 8.3 fluidounces, and the US legal cup, 240 mL^[4]. This is all a good reason to switch to the metric system, and cook by weights (as the rest of the world does), not volumes. Clearly, it makes no sense to record the volume of sugar as 4.00 cups rather than 4 cups!

Pousse Cafe

An after dinner drink called a Pousse Cafe ^[5] is made from from bottom to top, red grenadine, yellow chartreuse and green chartreuse. This can be simulated by coloring sugar water of different concentrations ^[6] It demonstrates how less dense liquids float on more dense liquids, if they're kept from mixing by carefully and slowing pouring them.

A sugar water pousse cafe

Maple Syrup

Sugar maple sap is boiled down, and as the water evaporates, the sugar concentration rises to 1333 kg/m³, the proper density, which corresponds to at least 66% sugar. An instrument called a hydrometer is simply floated in the syrup to indicate the density. If the density is too low the syrup will spoil, and if it's too high the syrup will crystallize. ^[7].

Note that unlike mass or volume, the density of a substance is independent of the size of the sample. Thus density is a property by which one substance can be distinguished from another. We can have 1 ml or 10 gallons of the syrup in Example 1, but its density will always be 1.15/cm³ at room temperature. The densities of some common pure substances are listed below.

Useful Density Values

Density is useful in cooking in other ways. Aluminum cookware may be chosen because it is so much less dense (2.70 g/cc) than iron (7.87 g/cc), copper (8.96), although there are other reasons for choosing cookware (see Cooking Efficiencies of Pots and Pans). The following table lists some density values for gases, liquids, and solids.

Tables and graphs are designed to provide a maximum of information in a minimum of space. When a physical quantity (number × units) is involved, it is wasteful to keep repeating the same units. Therefore it is conventional to use pure numbers in a table or along the axes of a graph. A pure number can be obtained from a quantity if we divide by appropriate units. For example, when divided by the units gram per cubic centimeter, the density of aluminum becomes a pure number 2.70:

$\dfrac{\text{Density of aluminum}} {\text{1 g cm}^{-3}} = \dfrac{\text{2.70 g cm}^{-3}} {\text{1 g cm}^{-3}} = 2.70$

Table $\PageIndex{1}$ : Density of Several Substances at 20°C.
Substance	Density / g cm^-3
Helium gas	0.000 16
Dry air	0.001 185
Gasoline	0.66-0.69 (varies)
Kerosene	0.82
Benzene	0.880
Water	1.000
Honey	1.44
Corn Syrup	1.48
Maple syrup	1.33
Magnesium	1.74
Salt	2.16
Aluminum	2.70
Iron	7.87
Copper	8.96
Silver	10.5
Lead	11.34
Uranium	19.05
Gold	19.32

Therefore, a column in a table or the axis of a graph is conveniently labeled in the following form:

$\dfrac{\text{Quantity}}{\text{units}}$

This indicates the units that must be divided into the quantity to yield the pure number in the table or on the axis. This has been done in the second column of the table.

Converting Densities

In our exploration of Density, notice that chemists may express densities differently depending on the subject. The density of pure substances may be expressed in kg/m³ as in the Maple Syrup paragraph above; the density of a cell may be expressed in mg/µL; and densities of solids like flour may be expressed in lb/ft³ in some agricultural or culinary tables. The density of flour varies from about 110 to about 170 g/cup, depending on the type of flour and how it is measured (that's another reason to cook by mass rather than volume of ingredients). It is easy to transform densities from one set of units to another, by multiplying the original quantity by one or more unity factors:

Example $\PageIndex{2}$ : Density Conversion

Convert the density of water, 1 g/cm³ to (a) lb/cm³ and (b) lb/ft³ and (c) g/cup. This last value is important to cooks: International recipies specify liquids by mass rather than volume, and most liquids have densities close to that of water, so knowing the mass of a cup of water is useful.

Solution

a. The equality 454 g = 1 lb can be used to write two unity factors,

$\dfrac{\text{454 g}} {\text{1 lb}}$ or $\dfrac{\text{1 lb}} {454}$

The given density can be multiplied by one of the unity factors to get the desired result. The correct conversion factor is chosen so that the units cancel:

$\dfrac{\text{1 g}} {\text{cm}^{3}}* \dfrac{\text{1 lb}} {\text{454 g}} = 0.002203 \dfrac{\text{lb}} {\text{cm}^{3}}$

b. Similarly, the equalities 2.54 cm = 1 inch, and 12 inches = 1 ft can be use to write the unity factors:

$\dfrac{\text{2.54 cm}} {\text{1in}}$ , $\dfrac{\text{1 in}} {\text{2.54 cm}}$ , $\dfrac{\text{12 in}} {\text{1 ft}}$ and $\dfrac{\text{1 ft}} {\text{12 in}}$

In order to convert the cm³ in the denominator of 0.002203 $\dfrac{lb} {cm^{3}}$ to in³, we need to multiply by the appropriate unity factor three times, or by the cube of the unity factor:

$\text{0.002203} \dfrac{\text{g}} {\text{cm}^{3}}$ x $\dfrac{\text{2.54 cm}} {\text{1 in}}$ x $\dfrac{\text{2.54 cm}} {\text{1in}}$ x $\dfrac{\text{2.54 cm}} {\text{1in}}$

$\text{0.002203} \dfrac{\text{g}} {\text{cm}^{3}}$ x $(\dfrac{\text{2.54 cm}} {\text{1 in}})^{3} = \text{0.0361} \dfrac{\text{lb}}{\text{in}}^3$

This can then be converted to lb/ft³:

$\text{0.0361} \dfrac{\text{lb}} {\text{in}^{3}}$ x $(\dfrac{\text{12 in}} {\text{1 ft}})^{3} = \text{62.4} \dfrac{\text{lb}}{\text{ft}^3}$

It is important to notice that we have used conversion factors to convert from one unit to another unit of the same parameter

c. The equality 1 cup = 236.6 mL (see Example 1) can be used to write two unity factors,

$\dfrac{\text{236.6 mL}} {\text{1cup}}$ or $\dfrac{\text{1 cup}} {\text{236.6mL}}$

The given density can be multiplied by one of the unity factors to get the desired result. The correct conversion factor is chosen so that the units cancel:

$1\dfrac{\text{g}} {\text{cm}^{3}} * 1 \dfrac{\text{cm}^{3}} {\text{1 mL}} * \dfrac {\text{236.6 mL}} {\text{1 cup}} = \text{236.6} \dfrac{\text{g}} {\text{cup}}$

References

↑ en.Wikipedia.org/wiki/Food_preservation
↑ This, H. "Molecular Gastronomy, Exploring the Sciene of Flavor", Columbia University Press, NY, 2006, pp. 218-220
↑ Determination of Sugar Content in Commercial Beverages by Density: A Novel Experiment for General Chemistry Courses; S. K. Henderson , C. A. Fenn and J. D. Domijan, J. Chem. Educ., 1998, 75 (9), p 1122
↑ en.Wikipedia.org/wiki/Cup_(volume)
↑ en.Wikipedia.org/wiki/Pousse_caf%C3%A9
↑ for an online set of instruction for making a sugar Pousse Cafe see A.M. Helmenstine, thoughtco.com/rainbow-in-a-glass-density-demonstration-604258, also see references 4-7 in "Making a Chemical Rainbow", M. Angelin and O. Ramstrm, J. Chem. Educ., 2010, 87 (5), pp 504–506
↑ en.Wikipedia.org/wiki/Maple_syrup

Contributors and Attributions

Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.