The Uncertainty Principle: Electronic Synapses

The Heisenberg Uncertainty Principle is easily stated, but it obviously has had a huge impact our science. Here we'll look at the implications for neural conduction through lesser known electronic synapes. Electronic synapses are found throughout the nervous system, but they are less common than chemical synapses, through which neural transmitters like serotonin carry the signal. In electronic synapses, electrons carry the signal, so they can be faster, and possibly more reliable than chemical synapses.

The uncertainty principle states that the product of the uncertainty in momentum (P) and the position of a particle cannot be less than a constant expressed in terms of Planck's Constant, h:

\(\Delta X \Delta P \ge \dfrac{h}{4\pi}\)

Here Δ can be taken as the standard deviation, or random uncertainty in measurement. Planck's constant is h = 6.626 x 10^-34J s, but the uncertainty principle is sometimes expressed in terms of : \(\hbar\) , which is h/2π:

\(\Delta X \Delta P \ge \dfrac{\hbar}{2}\)

The Uncertainty Principle can be stated in terms of other complementary variables, like energy and time:

\(\Delta E \Delta t \ge \dfrac{\hbar}{2}\)

Example \(\PageIndex{1}\): Uncertainty of the Position of an Electron

Suppose we have an electrical synapse rather than a chemical synapse. Electrical synapses are not as common as chemical synapses, but are found throughout the nervous system. They provide a narrow gap between the pre- and postsynaptic cells of about 3.5 nm rather than the 20 to 40 nm distance of chemical synapses^[1]. If the electron is transmitted from one neuron to the other with a velocity of 5 x 10⁶ m/s (its speed in a hydrogen atom) and the speed is known to within 10% due to variable properties of the synapse, what is the uncertainty in the position of the electron?

The uncertainty in momentum is Δmv, and if the mass (9.11 x 10^-31 kg) is known with good precision, this is mΔv = 9.11 × 10^-31kg x 0.10 x 5 x 10⁶ m/s = 4.6 x 10^-25 kg m s^-1

\(\Delta X \Delta P \ge \dfrac{h}{4\pi}\)

\(\Delta X (\text{4.6} \times \text{10}^{-25} \text{kg*m/s} \ge \dfrac{\text{6.626} \times \text{10}^{-34} \text{J s}}{\text{4 (3.14)}}\)

\(\Delta X \ge \text{1.2} \times \text{10}^{-10} \text{m} \)

We're told that the entire synapse is 3.5 nm (3.5 x 10^-9 m), so the electron's position is localized in some 10% of the synaptic cleft. If no other factors (like chemical forces that direct the electron more precisely by decreasing the uncertainty in its motion) improve this localization, what do you conclude about the precision of neural transmission through electrical synapses?

Suppose that the electron in the example above were not in a synapse, but rather in a hydrogen atom, in one of the orbitals around the nucleus. We know that the hydrogen atom has a diameter of about 1 x 10^-10 m (100 pm), so the electron could be anywhere in that space if we assume the 10% uncertainty in speed (it would be delocalized over 10 atoms if we specified the velocity to 1%).

Our inability to locate an electron exactly may seem rather strange, but it arises whether we think in terms of waves or of particles. Suppose an experiment is to be done to locate a billiard ball moving across a pool table whose surface is hidden under a black cloth.

Figure \(\PageIndex{1}\) Determining the location and speed of a particle. (a) Locating a billiard ball (X)by bouncing a second billiard ball (Y) off it; (b) locating a billiard ball by bouncing a table-tennis ball off it; (c) locating a billiard ball by bouncing photons of visible off it; (d) locating an electron by bouncing a photon off it.

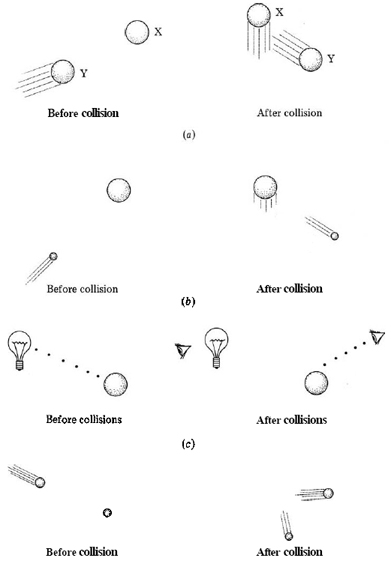
One way to do this would be to try to bounce a second billiard ball off the first one (Fig. \(\PageIndex{1}\). When a hit was made and the second ball emerged from under the cloth, we would have a pretty good idea of where the first ball was. The only trouble with the experiment is that the position and speed of the first ball would almost certainly be changed by the collision. To lessen this effect, a table-tennis ball could be substituted for the second billiard ball—its smaller mass would produce a much smaller change in the motion of the first ball. Clearly, the lighter and more delicate the “probe” we use to try to locate the first ball, the less our measurement will affect it. The best way to locate the first billiard ball and determine its speed would be to remove the cover from the table so it could be seen. In this case, however, something is still “bouncing” off the first billiard ball (Fig. \(\PageIndex{1}\)c). If we are to see the ball, particles of visible light, or photons, must strike the ball and be reflected to our eyes. Since each photon is very small and has very little energy by comparison with that needed to change the motion of the billiard ball, looking at a ball is an excellent means of observing it without changing its position or speed.

But to observe an electron is quite another story, since the mass of an electron is far smaller than that of a billiard ball. Anything (such as a photon of light) which can be bounced off an electron in such a way as to locate it precisely would have far more energy than would be required to change the path of the electron. Hence it would be impossible to predict the electron’s future speed or position from the experiment. The idea that it is impossible to determine accurately both the location and the speed of any particle as small as an electron is called the uncertainty principle. It was first proposed in 1927 by Werner Heisenberg (1901 to 1976).

According to the uncertainty principle, even if we draw an analogy between the electron in a box and a billiard ball (Fig. 1a in Wave Mechanics), it will be impossible to determine both the electron’s exact position in the box and its exact speed. Since kinetic energy depends on speed (½ mu²) and Eq. (4) in Wave Mechanics assigns exact values of kinetic energy to the electron in the box, the speed can be calculated accurately. This means that determination of the electron’s position will be very inexact. It will be possible to talk about the probability that the electron is at a specific location, but there will also be some probability of finding it somewhere else in the box. Since it is impossible to know precisely where the electron is at a given instant, the question, “How does it get from one place to another?” is pointless. There is a finite probability that it was at the other place to begin with!

It is possible to be quantitative about the probability of finding a “billiard-ball” electron at a given location, however. Shortly after the uncertainty principle was proposed, the German physicist Max Born (1882 to 1969) suggested that the intensity of the electron wave at any position in the box was proportional to the probability of finding the electron (as a particle) at that same position. Thus if we can determine the shapes of the waves to be associated with an electron, we can also determine the relative probability of its being located at one point as opposed to another. The wave and particle models for the electron are thus connected to and reinforce each other. Niels Bohr suggested the term complementary to describe their relationship. It does no good to ask, “Is the electron a wave or a particle?” Both are ways of drawing an analogy between the microscopic world and macroscopic things whose behavior we understand. Both are useful in our thinking, and they are complementary rather than mutually exclusive.

A graphic way of indicating the probability of finding the electron at a particular location is by the density of shading or stippling along the length of the box. This has been done in Fig. \(\PageIndex{2}\) for the same three electron waves previously illustrated in Fig. 1 from Wave Mechanics. Notice that the density of dots is large wherever the electron wave is large.(This would correspond in the guitar-string analogy to places where the string was vibrating quite far from its rest position.)

Figure \(\PageIndex{2}\) Indicating electron density or electron probability by the density of dots for the electron in a box. Nodes. where the probability of finding the electron is zero, are indicated. In the guitar-string analogy a node corresponds to a point on the string which is not vibrating up and down.

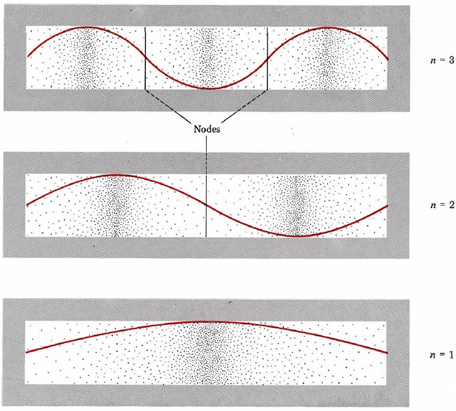
Where the electron wave is small (near the ends of the box in all three cases and at the nodes indicated in the figure), there are only a small number of dots. (A node is a place where the intensity of the wave is zero, that is, in the guitar-string analogy, where the string has not moved from its rest position.)

If the electron is thought of as a wave occupying all parts of the box at once, we can speak of an electron cloud which has greater or lesser density in various parts of the box. There will be a greater quantity of negative charge in a region of high density (a region where there is a greater concentration of dots) than in one of low density. In an atom or molecule, according to the uncertainty principle, the best we can do is indicate electron density in various regions—we cannot locate the precise position of the electron. Therefore electron dot-density diagrams, such as the ones shown in Fig. \(\PageIndex{2}\), give a realistic and useful picture of the behavior of electrons in atoms. In such a diagram the electron density or probability of finding the electron is indicated by the number of dots per unit area. We will encounter electron dot-density diagrams quite often throughout this book. These have all been generated by a computer from accurate mathematical descriptions of the atom or molecule under discussion.

From ChemPRIME: 5.5: The Uncertainty Principle

References

1. ↑ TAG Heuer ReplicaTAG Heuer Replica

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.