Protein Nutrition

Vegetarian Diets

Although a vegetarian diet has many health and environmental advantages, some people worry that they will get insufficient protein in their diet if they exclude meat. But to produce 1 pound of protein in the form of beef or veal, we must feed 21 pounds of vegetable protein to the animal (not to mention gallons of water). It may be that the amount of protein lost to humans in this way is equivalent to 90% of the annual world protein deficit. In the contemporary US it is virtually impossible to suffer protein malnutrition no matter what our diet (we generally eat a huge excess of protein), but in some poorly developed nations certain vegetarian diets may not supply enough protein, even though they provide enough calories, and diseases like kwashiorkor are common. There is animal evidence for increase in disease when single amino acids are deficient ^[1].

Figure \(\PageIndex{1}\) Kwashiorkor victim^[2]

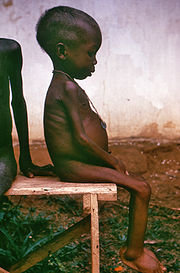
Limiting Reactants in Protein Biosynthesis

Nutritionists look to chemists to explain protein deficiency in terms of amino acid composition of foods and "Limiting Reactants". When a limiting reactant is used up, the other reactants, no matter how plentiful they are, have nothing to react with, so the reaction ceases and the left over reactants are wasted.

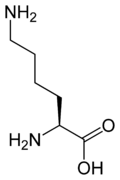
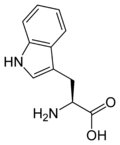
Human proteins are complex polymers ("polypeptides") made by joining about 8 essential amino acids that our bodies can't synthesize (and aother 12 that our bodies synthesize) in particular orders that define the activity of a protein (which may be an enzyme, a structural body component, or serve many other functions). Molecular structures of two essential amino acids, lysine and tryptophan, are shown here.

Figure \(\PageIndex{2}\) The lysine molecule ^[3]

Figure \(\PageIndex{3}\) The tryptophan molecule^[4]

The amino acids are joined by a very simple "condensation" reaction where two molecules join by eliminating water, as shown in the figure below. The portion of the molecule labeled "R" stands for a variable part of the molecule that distinguishes different amino acids; the rest of the molecule is common to all amino acids.

This process can continue with different amino acids adding to either end of the protein chain. The H-N of an amino acid adds to the C-OH end of the protein, eliminating water (H-OH) and forming a C-N bond where the water was eliminated (or the C-OH end of an amino acid adds to the N-H end of the protein). This process continues until the protein has hundreds of different amino acids.

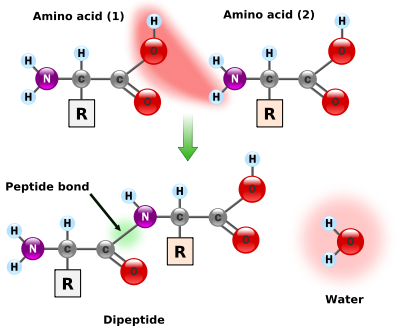
Figure \(\PageIndex{4}\) Formation of a peptide bond ^[5]

Example \(\PageIndex{1}\): Peptide Bonding

Show two ways that one lysine molecule and one tryptophan molecule can combine via a peptide bond.

Solution In the figure showing the formation of a peptide bond, we see that two amino acids are different only because they have different "R" groups. The "R" group of lysine is -CH₂CH₂CH₂NH₂, and that of tryptophan is -CH₂C₈H₆N (with the fused 5 and 6 atom rings). It's always the terminal acid (-COOH) and alpha amino acid (-NH₂ on the adjacent carbon atom) that react to form the peptide bond. If we replace "R" on the left amino acid with -CH₂CH₂CH₂NH₂ it becomes lysine. Replacing "R" on the right amino acid with -CH₂C₈H₆N we get tryptophan, and the amine (-NH₂) group of tryptophan bonds to the acid group (-COOH) of lysine. If we switch the "R" groups, then the amine group of the lysine on the right will bond with the acid group of the tryptophan on the left to make a different dipeptide.

We can understand why a vegetarian diet with plenty of calories could cause protein malnutrition by imagining simple vegetable proteins that contained only two amino acids, lysine (abbreviated LYS) and tryptophan (TRP), which are consumed by a person and must be used to make human protein. This example is highly simplified to demonstrate a principle; the actual synthesis of human protein from vegetable is much more complex.

Example \(\PageIndex{2}\): Determining the Limiting Reagent

A legume food provides 100.0 g of and 100.0 g of tryptophan, but the Human polypeptide requires equal amounts of each. Which is the limiting reagent?

Solution The balanced equation

LYS + TRP → (LYS₁TRP₁)_n + n H₂O

tells us that according to the atomic theory, 1 mol LYS is required for each mole of TRP to make a long chain polypeptide with a large number "n" of repeating LYS-TRP units: ~LYS-TRP-LYS-....TRP~ . That is, the stoichiometric ratio S(LYS/TRP) = 1 mol LYS / 1 mol TRP. Let us see how many moles of each we actually have in the legume food. By inspecting the molecular structure, we see that LYS is C₆H₁₄N₂O₂ and has a molar mass M = 146.19 g mol^-1 and similarly TRP is C₁₁H₁₂N₂O₂ has M = 204.23 g mol^-1.

\(n_{TRP} = \text{100.0 g} \times \dfrac{\text{1 mol TRP}}{\text{204.23 g}} = \text{0.4896 mol TRP}\)

\(n_{LYS} = \text{100.0 g} \times \dfrac{\text{1 mol LYS}}{\text{146.19 g}} = \text{0.684 mol LYS}\)

When the reaction ends, 0.4896 mol TRP will have reacted with 0.4896 mol LYS and there will be

\(\text{(0.6840 - 0.4896) mol LYS} = \text{0.195 mol LYS}\)

left over. TRP is therefore the limiting reagent, and 0.1273 mol (about 19 g or 20% of the total) is entirely wasted.

But suppose at the same time that the legume was consumed, a serving of wheat was also consumed that provided 140 g of TRP and only 71.5 g of LYS (wheat is notoriously low in LYS, just as legumes are high in LYS). Now

\(n_{TRP} = \text{140.0 g} \times \dfrac{\text{1 mol TRP}}{\text{204.23 g}} = \text{0.685 mol TRP}\)

\(n_{LYS} = \text{72.9 g} \times \dfrac{\text{1 mol LYS}}{\text{146.19 g}} = \text{0.489 mol LYS}\)

Now there is 0.196 mol of TRP left over from the wheat protein, exactly enough to react with the excess LYS from the legumes, and no amino acid is wasted! Thus wheat and beans are complementary sources of protein, and if eaten together, provide optimal nutrition, as shown in the diagram below, where the deficiencies in each cause neither to be fully utilized, but when eaten together, about equal amounts of the four amino acids are provided, which leads to essentially perfect stoichiometric ratios for synthesis of human protein.

Figure \(\PageIndex{5}\): Amino Acid Content of Foods

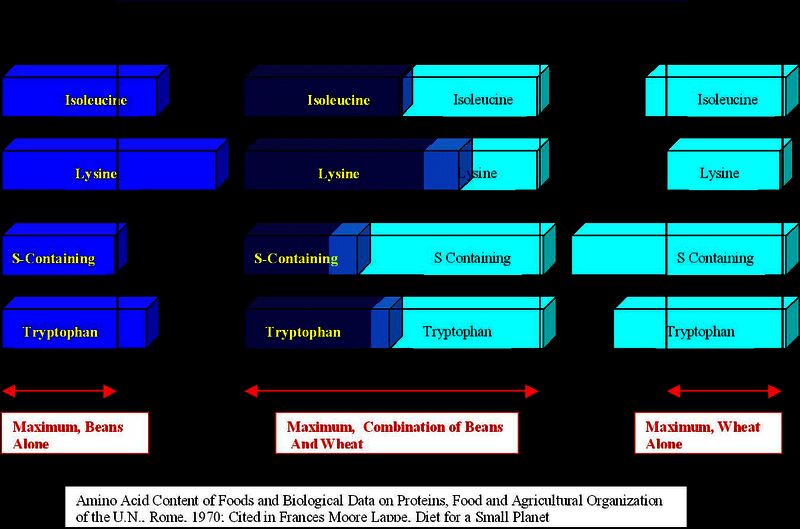
Complementary Amino Acids

In order to design a proper diet, complementary protein foods would have to be chosen from tables of amino acid contents of foods. Some anthropologists notice how often diets of complementary foods show up in different parts of the world (i.e. tacos and beans), and attribute the society's survival value to their choice of food.

From the legume example you can begin to see what needs to be done to determine which of two reagents, X or Y, is limiting. We must compare the stoichiometric ratio S(X/Y) with the actual ratio of amounts of X and Y which were initially mixed together. In Example 1 this ratio of initial amounts

\(\dfrac{n_{TRP} (initial)}{n_{LYS} (initial)} = \dfrac{\text{0.4986 mol TRP}}{\text{0.6840 mol LYS}} = \dfrac{\text{0.716 mol TRP}}{\text{1 mol LYS}}\)

was greater than the stoichiometric ratio

\(\text{S}\dfrac{\text{TRP}}{\text{LYS}} = \dfrac{\text{1 mol TRP}}{\text{1 mol LYS}}\)

This indicated that there was not enough TRP to react with all the LYS and TRP was the limiting reagent. The corresponding general rule, for any reagents X and Y, is

If \(\dfrac{n_{x} (initial)}{n_{y}(initial)}\) is less than \(\text{S}\dfrac{X}{Y}\) then X is limiting.

If \(\dfrac{n_{x} (initial)}{n_{y}(initial)}\) is greater than \(\text{S}\dfrac{X}{Y}\) then Y is limiting.

These calculations can be organized as a table, with entries below the respective reactants and products in the chemical equation. Calculations are shown for each possible case, assuming that one reactant is completely consumed and determining if enough of the other reactants is present to consume it. If not, that scenario is discarded.

	LYS	+ TRP →	(LYS1TRP1)n	+ n H2O
m (g)	100	100
M (g/mol)	146.19	204.23
n (mol)	0.684	0.490
if all LYS reacts	-0.684	-0.684
if all TRP reacts	-0.490	-0.490
Actual Reaction Amounts	-0.490	-0.490
Actual Reaction Masses	-71.6	-100

(Of course, when the amounts of X and Y are in exactly the stoichiometric ratio, both reagents will be completely consumed at the same time, and neither is in excess.). This general rule for determining the limiting reagent is applied in the next example.

Example \(\PageIndex{3}\): Limiting Reagent

To detect an amino acid (even in a fingerprint in forensic chemistry), the ninhydrin test is often used.

Ninhydrin

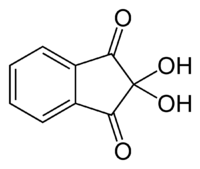
In the ninhydrin test, two ninhydrin molecules (C₉H₆O₄, shown to the left) become linked by the N attached to the first carbon of the amino acid chain, producing the blue/purple ion shown below.

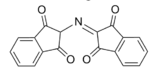Blue/Purple Product^[6]

The balanced chemical equation is:

\(\ce{2C9H6O4 + C11H12N2O2 -> (C9H5O2)--N=(C9H4O2) + C10H9NO + CO2 + 3H2O}\)

If 2.00 mg of ninhydrin (Nin) is used to detect 2 mg of TRP, has enough ninhydrin been added to react with all the TRP? Which is the limiting reagent, and what mass of H₂O will be formed?

Solution

The stoichiometric ratio connecting Nin and TRP is

\(\text{S}\dfrac{\text{Nin}}{\text{TRP}} = \dfrac{\text{2 mol Nin}}{\text{1 mol TRP}}\)

The initial amounts of Nin and TRP are calculated using appropriate molar masses(160.13 g mol⁻¹ for Nin and 204.23 g mol⁻¹ for TRP:

\(n_{Nin}(initial) = \text{2.00} \times \text{10}^{-3} \text{g} \times \dfrac{\text{1 mol Nin}}{\text{178.14 g}} = \text{1.12} \times \text{10}^{-5} \text{mol Nin}\)

\(n_{TRP}(initial) = \text{2.00} \times \text{10}^{-3} \text{g} \times \dfrac{\text{1 mol TRP}}{\text{204.23 g}} = \text{9.79} \times \text{10}^{-6} \text{mol TRP}\)

Their ratio is

\(\dfrac{n_{Nin} (initial)}{n_{TRP} (initial)} = \dfrac{\text{1.123} \times \text{10}^{-5} \text{mol Nin}}{\text{9.79} \times \text{10}^{-6} \text{mol TRP}} = \dfrac{\text{1.15 mol Nin}}{\text{1 mol TRP}}\)

Since this ratio is smaller than the 2:1 stoichiometric ratio, you have insufficient Nin to react with all the TRP, so Nin is the limiting reagent. To ensure detection, in would be better to add excess Ninhydrin.

b) The amount of water product formed in a reaction may be calculated via an appropriate stoichiometric ratio from the amount of a reactant which was consumed. Some of the excess reactant TRP will be left over, but all the initial amount of Nin will be consumed. Therefore we use n_Nin (initial) to calculate how much H₂O can be obtained

\[ n_{\text{Nin}}\text{ }\xrightarrow{S\text{(water/Nin)}}\text{ }n_{\text{water}}\xrightarrow{M_{\text{water}}}\text{ }m_{\text{water}}\]

\(m_{water} = \text{1.12} \times \text{10}^{-5} \text{mol Nin} \times \dfrac{\text{3 mol water}}{\text{2 mol Nin}} \times \dfrac{\text{18.016 g}}{\text{1 mol water}} = \text{3.02} \times \text{10}^{-4} \text{ g water} \)

This is 0.302 mg water.

These calculations can be organized as a table, with entries below the respective reactants and products in the chemical equation. Calculations are shown for each possible case, assuming that one reactant is completely consumed and determining if enough of the other reactants is present to consume it. If not, that scenario is discarded.

	2 C9H6O4	+ C11H12N2O2 →	(C9H5O2)-N=(C9H4O2))	+ C10H9NO	+ CO2	+ 3 H2O
m (g)	0.0020	0.0020
M (g/mol)	178.1	204.23	303.3	159.2	44.0	18.0
n (mol)	1.12 x 10^-5	9.79 x 10^-6	--	--	--	--
if all C9H6O4 reacts	-1.12 x 10^-5	-5.62 x 10^-6
if all C11H12N2O2 reacts	-1.96 x 10^-5	-9.79 x 10^-6
Actual Reaction Amounts	-1.12 x 10^-5	-5.62 x 10^-6	5.62 x 10^-6	5.62 x 10^-6	5.62 x 10^-6	1.68 x 10^-5
Actual Reaction Masses	-0.0020	-0.00115	1.71 x 10^-3	8.93 x 10^-4	2.47 x 10^-4	3.02 x 10^-4

As you can see from the example, in a case where there is a limiting reagent, the initial amount of the limiting reagent must be used to calculate the amount of product formed. Using the initial amount of a reagent present in excess would be incorrect, because such a reagent is not entirely consumed.

The concept of a limiting reagent was used by the nineteenth century German chemist Justus von Liebig (1807 to 1873) to derive an important biological and ecological law. Liebig’s law of the minimum states that the essential substance available in the smallest amount relative to some critical minimum will control growth and reproduction of any species of plant or animal life. When a group of organisms runs out of that essential limiting reagent, the chemical reactions needed for growth and reproduction must stop. Vitamins, protein, and other nutrients are essential for growth of the human body and of human populations. Similarly, the growth of algae in natural bodies of water such as Lake Erie can be inhibited by reducing the supply of nutrients such as phosphorus in the form of phosphates. It is for this reason that many states have regulated or banned the use of phosphates in detergents and are constructing treatment plants which can remove phosphates from municipal sewage before they enter lakes or streams.

From ChemPRIME: 3.2: The Limiting Reagent

References

1. ↑ http://jem.rupress.org/cgi/content/abstract/137/1/1
2. ↑ en.Wikipedia.org/wiki/Kwashiorkor
3. ↑ en.Wikipedia.org/wiki/Lysine
4. ↑ en.Wikipedia.org/wiki/Tryptophan
5. ↑ en.Wikipedia.org/wiki/Amino_acid
6. ↑ en.Wikipedia.org/wiki/Ninhydrin

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.