2.4.D: Periodic Trends

Introduction

Trends across a period follow from the increasing number of protons in the nucleus and the decrease in radius. Both contributions can be explained by the change in effective nuclear charge.

Trends down a group follow from the increasing number of electron shells and the increased distance of the outer electrons from the nucleus. The major factor is the increasing size.

The properties of an element are largely determined by their electronic configurations, giving rise to recurring patterns or periodic behaviour. Examples are shown in the diagrams below including ionization energy, electron affinity, electronegativity and atomic radii. It is this periodicity of properties, manifestations of which were noticed well before the underlying theory was known, that led to the establishment of the periodic law (the properties of the elements recur at varying intervals) and the development of the first periodic tables. The modern periodic table is a tabular arrangement of the chemical elements, organized on the basis of their atomic number (number of protons in the nucleus), electronic configurations, and recurring chemical properties.

In the RSC Tutorial Chemistry Text on Main Group Chemistry, it notes that "When an element forms a chemical compound, electrons can be considered to be either lost, gained or shared with other atoms. These tendencies can be assessed by the parameters of ionization energy (IE), electron affinity (EA) and electronegativity (E). Prediction of bond types as either ionic or covalent then allows prediction of the chemical and physical properties of chemical substances."

So how are these parameters defined and how do they vary with atomic number?

Effective nuclear charge

The concept of the effective nuclear charge (often symbolized as Z_eff or Z^*) relates to the net positive charge experienced by an electron in a multi-electron atom. The term "effective" is used because the shielding effect of negatively charged inner electrons prevents higher orbital electrons from experiencing the full nuclear charge due to the repelling effect of the lower inner-layer electrons.

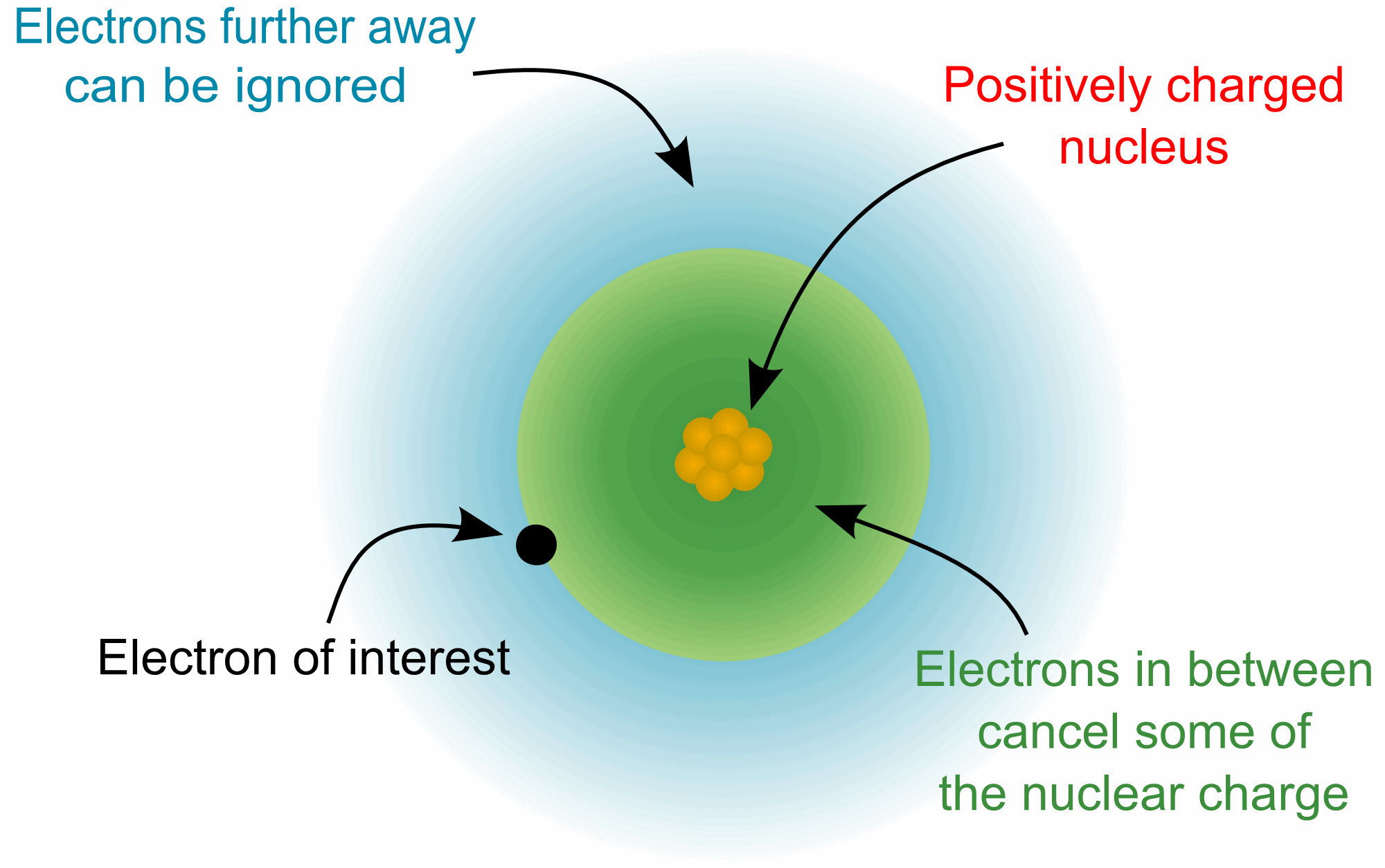In an atom with one electron, that electron experiences the full charge of the positive nucleus. In this case, the effective nuclear charge can be calculated from Coulomb's law.

However, in an atom with many electrons the outer electrons are simultaneously attracted to the positive nucleus and repelled by the inner negatively charged electrons. The effective nuclear charge on such an electron is given by the following equation:

Z_eff = Z - S

where
Z is the number of protons in the nucleus (atomic number), and
S is the shielding calculated from the electrons between the nucleus and the electron in question. A systematic method for determining this is given by "Slater's rules".

These can be summarised as follows:
Arrange the electrons into a sequence of groups in order of increasing principal quantum number n, and for equal n in order of increasing azimuthal quantum number l, except that s- and p- orbitals are kept together.

[1s] [2s,2p] [3s,3p] [3d] [4s,4p] [4d] [4f] [5s, 5p] [5d] etc.

Any electron higher in the sequence to the electron under consideration contributes nothing to the shielding, S, and is ignored.

For an electron in an ns or np orbital:

0.35 comes from each other electron within the same group except for the [1s] group, where the other electron contributes only 0.30.

0.85 for each electron with principal quantum number n one less than that of the group, i.e (n-1) shell

1.00 for each electron with principal quantum number two or more less, i.e (n-2) etc. shell

For an electron in an nd or nf orbital:
0.35 comes from each other electron within the same group

1.00 for each electron "closer" to the atom than the group. This includes electrons with the same principal quantum number but in s or p orbitals.

In tabular form, the rules are summarized as:

Group	Other electrons in the same group	Electrons in group(s) with principal quantum number n and azimuthal quantum number < l	Electrons in group(s) with principal quantum number n-1	Electrons in all group(s) with principal quantum number < n-1
[1s]	0.30	-	-	-
[ns, np]	0.35	-	0.85	1
[nd] or [nf]	0.35	1	1	1

Example 1.
Consider a sodium cation, Na⁺, a fluorine anion, F^-, and a neutral neon atom, Ne. Each has 10 electrons, 1s² 2s² 2p⁶ so the shielding from the 1s and 2s/2p electrons is 2 * 0.85 + 7 * 0.35 = 4.15 but the effective nuclear charge varies because each has a different atomic number:

Z_eff F^- = 9 - 4.15 = 4.85
Z_eff Ne = 10 - 4.15 = 5.85
Z_eff Na⁺ = 11 - 4.15 = 6.85

So the sodium cation has the largest effective nuclear charge, and can be expected to have the smallest radius.

Example 2.
Predict whether K would be more energetically stable with a configuration of
1s² 2s² 2p⁶ 3s² 3p⁶ 4s¹ or 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹

For K, Z=19 and considering the 4s electron then the screening constant S can be calculated from:

S= (8 * 0.85) + (10 * 1.0) = 16.8

Z_eff = 19 - 16.8 = 2.2

For the 3d calculation of S:

S= (18 * 1.0) = 18

Z_eff = 19 - 18 = 1

Accordingly, an electron in the 4s (as opposed to the 3d) orbital would come under the influence of a greater effective nuclear charge in the ground state of potassium and so will be the orbital that is occupied.

Ionization Energy

The Ionization Energy (IE_n) of an element is defined as the internal energy change associated with the removal of an electron from the gaseous atom, E, in its ground state, i.e. at 0 K. The first IE is therefore the energy required for the reaction:
E_(g) → E⁺_(g) + e^- energy required = IE

This energy change is generally considered equivalent to the enthalpy change at 298 K (ΔH_{298 K}). Estimates of the error suggest < 10 kJmol^-1 which when compared to typical IE values often in their thousands, is insignificant.

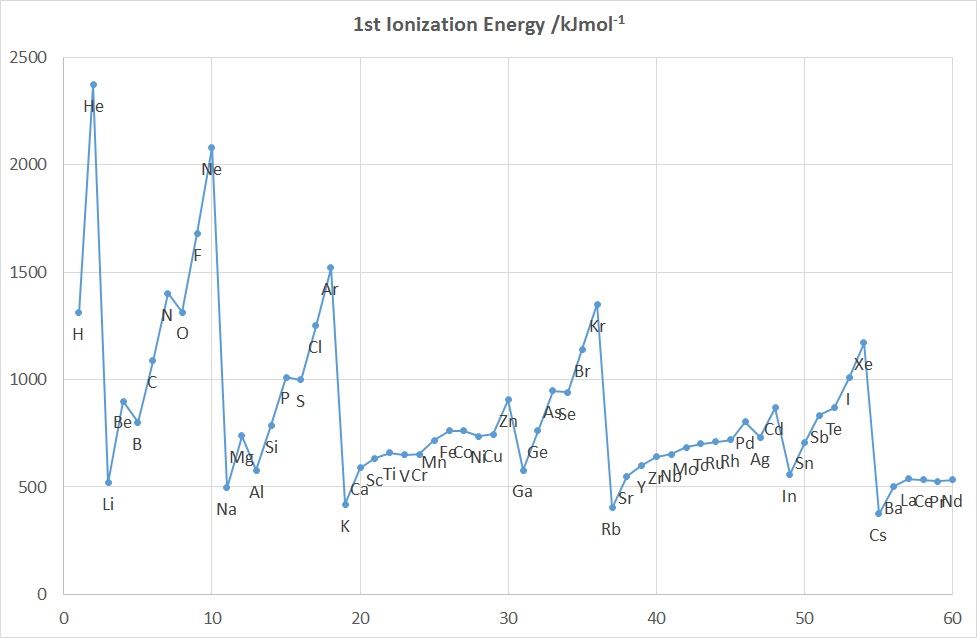
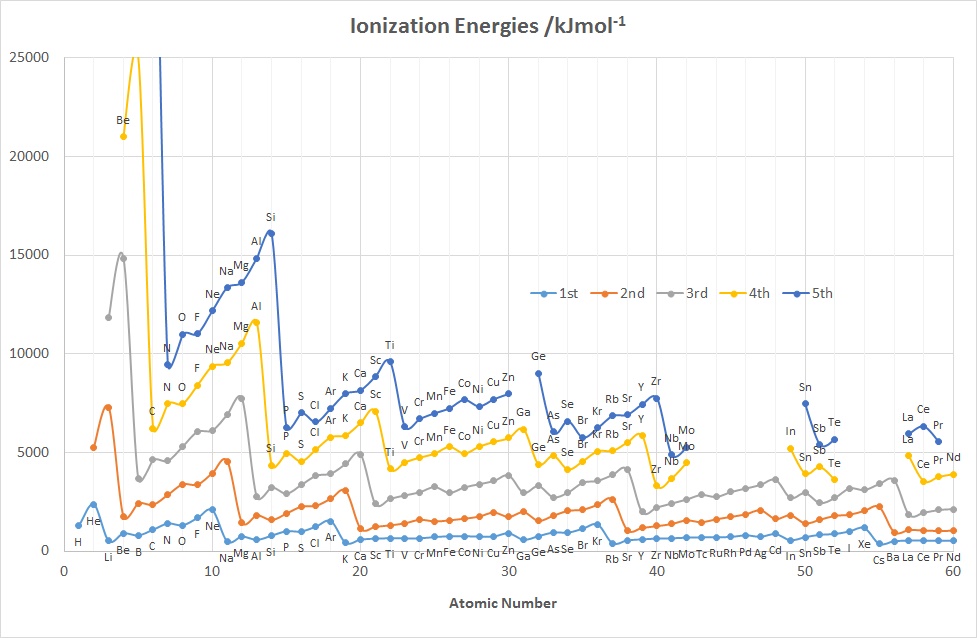The diagrams above show the variation in the values of the 1st five IE's as a function of Z up to Nd (60).

Features to note for IE₁ are:

• the values associated with the noble gases are the highest in each period
• the values associated with the group 1 elements are generally the lowest in each period, (group 2 elements for the 2nd IE and group 3 for the 3rd IE etc.)
• the gradual increase in values across a given period (applies to IE_2-5 as well)
• the drop in values on going from an element in group 15 to its neighbour in group 16 e.g. for N-O, P-S, As-Se
• the drop in values on going from an element in group 2 or 12 to its neighbour in group 13, e.g. for Be-B, Mg-Al and Zn-Ga, Cd-In
• the rather similar values for a given row of d-block elements

These observations can be accounted for in terms of the effective nuclear charge since the further away from the positively charged nucleus that a negatively charged electron is located, the less strongly that electron is attracted to the nucleus and the more easily it can be removed. So, as the atomic radius decreases from left to right across the Period the 1st Ionization Energy increases.

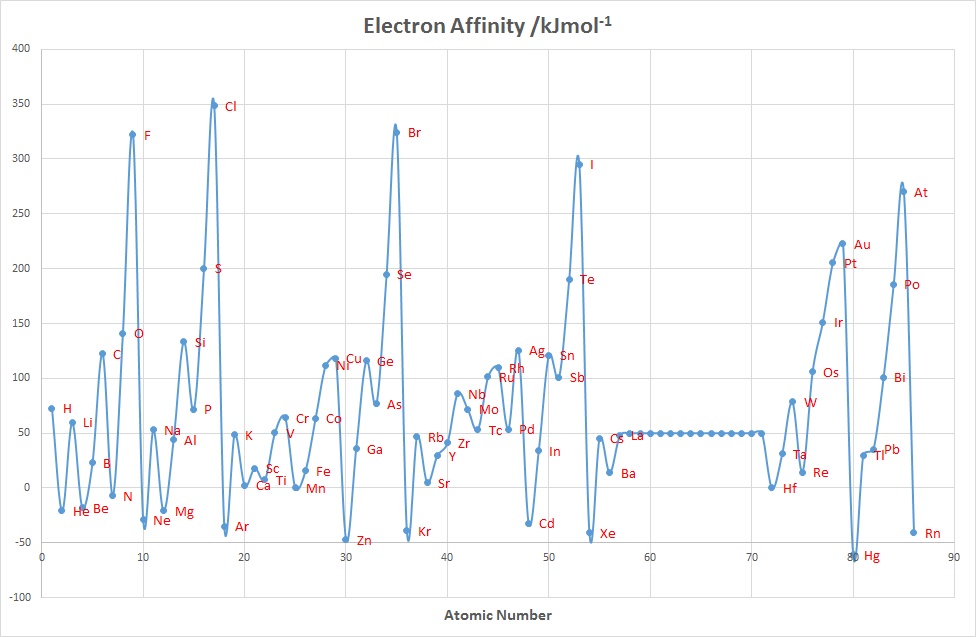
Electron Affinity

The electron affinity(EA) of an element E is defined as minus the internal energy change associated with the gain of an electron by a gaseous atom, at 0 K :

\[E_{(g)} + e^- → E^-_{(g)}\]

Unlike ionization energies, which are always positive for a neutral atom because energy is required to remove an electron, electron affinities can be positive (energy is released when an electron is added), negative (energy must be added to the system to produce an anion), or zero (the process is energetically neutral).

Chlorine has the most positive electron affinity of any element, which means that more energy is released when an electron is added to a gaseous chlorine atom than to an atom of any other element, EA= 348.6 kJmol^-1 and the Group 17 elements have the largest values overall. The addition of a second electron to an element is expected to be much less favored since there will be repulsion between the negatively charged electron and the overall negatively charged anion. For example, for O the values are:

\[O_{(g)} + e^ \rightarrow O^-_{(g)} \;\;\;\; EA = +141\; kJmol^{-1}\]

\[O^-_{(g)} + e^- → O^{2-}){(g)} \;\;\;\; EA = -798\; kJmol^{-1}\]

Electronegativity

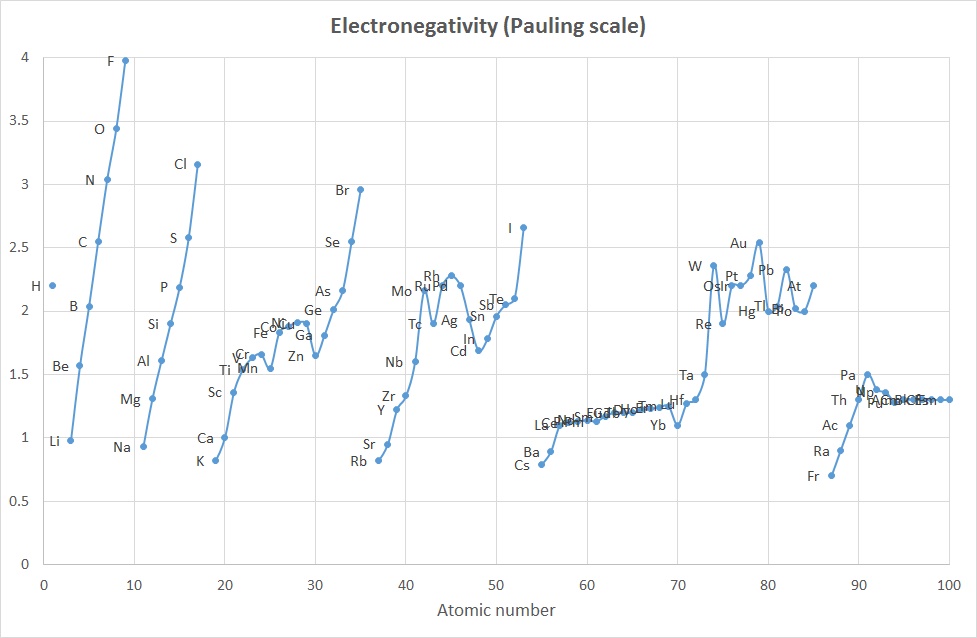
The concept of Electronegativity originated with Linus Pauling in the 1930's and was defined as "the power of an atom in a molecule to attract electrons to itself".

The values proposed by Pauling were calculated based on differences in bond dissociation enthalpy values found when comparing homo-diatomic molecues with hetero-diatomic molecules. For example , the bond energy of chlorine monofluoride, ClF, is about 255 kJ mol^-1 which is significantly greater than for either of the two homo-nuclear species Cl₂ and F₂ (242 and 153 kJ mol^-1 respectively). Pauling attributed this to an electrostatic attraction between the partially charged atoms in the heternuclear species. That is the excess bond energy came from an ionic contribution to the bond.

The method of calculating the Pauling values is:

D(XY) = [D(XX).D(YY)]^1/2 + 96.48 * (χ_Y - χ_X)² where the 96.48 factor means D values are in kJ mol^-1

In Housecroft and Sharpe the average, rather than geometric mean is used, and this is rearranged to give:

ΔD = D(XY) - {½ * [D(XX) - D(YY)] } = (χ_Y - χ_X)² = (Δχ)²

or Δχ = √(ΔD)

As only differences in electronegativity were defined, it was necessary to choose an arbitrary reference point in order to construct a scale. Hydrogen was chosen as the reference, since it formed covalent bonds with a large variety of elements: its electronegativity was fixed at 2.20.

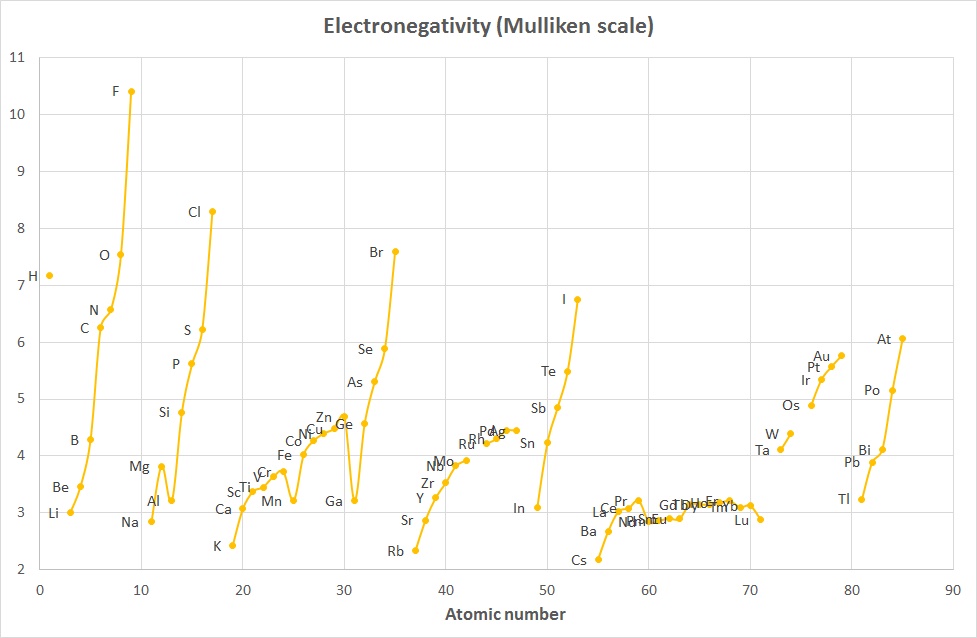
The Mulliken scale was calculated by taking the average of the Ionization Energy and the Electron Affinity (when both were given in units of eV).

χ^M = ½ (IE₁ + EA₁) where both IE₁ and EA₁ are in eV

A variant of this (2006) that converts the values to roughly the Pauling scale is:

χ^M = 0.00197 * (IE₁ + EA₁) + 0.19 where IE₁ and EA₁ are now given in kJ mol^-1

The plots above indicate that while the absolute values are different, the trends are quite similar and the 2 curves are comparable when scaled appropriately.

The Allred-Rochow scale considered that electronegativity was related to the charge experienced by an electron on the "surface" of an atom: the higher the charge per unit area of atomic surface the greater the tendency of that atom to attract electrons. Their scale was dependent on Z_eff and inversely proportional to the square of the covalent radius, r_cov.

χ^AR = (3590 * Z_eff / r²_cov) + 0.744 where r_cov is in pm

The values range between 0 and 10. Once again a good correlation to the Pauling scale was found and this applies as well to other Electronegativity scales.

Atomic Radius

Have a look at an interactive visual display (JSmol) showing the periodic table of elements with atomic and ionic radii.

The atomic radius of a chemical element is a measure of the size of its atoms, usually the mean or typical distance from the center of the nucleus to the boundary of the surrounding cloud of electrons. Since the boundary is not a well-defined physical entity, there are various non-equivalent definitions of atomic radius. Three widely used definitions of atomic radius are Van der Waals radius, ionic radius, and covalent radius.

Covalent radius is defined as half the covalent bond length when the two atoms bonded are homonuclear (½ X-X bond).

van der Waals radius is defined as half of the internuclear separation of two non-bonded atoms of the same element on their closest possible approach.

It is not possible to measure the sizes of both metallic and nonmetallic elements using a single technique and method. To get values for comparison, theoretical quantum mechanical functions have been used instead to calculate atomic radii.

In the periodic table, atomic radii decrease from left to right across a period and increase from top to bottom down the groups. As a result of these two trends, the largest atoms are found in the lower left corner of the periodic table, and the smallest are found in the upper right corner.

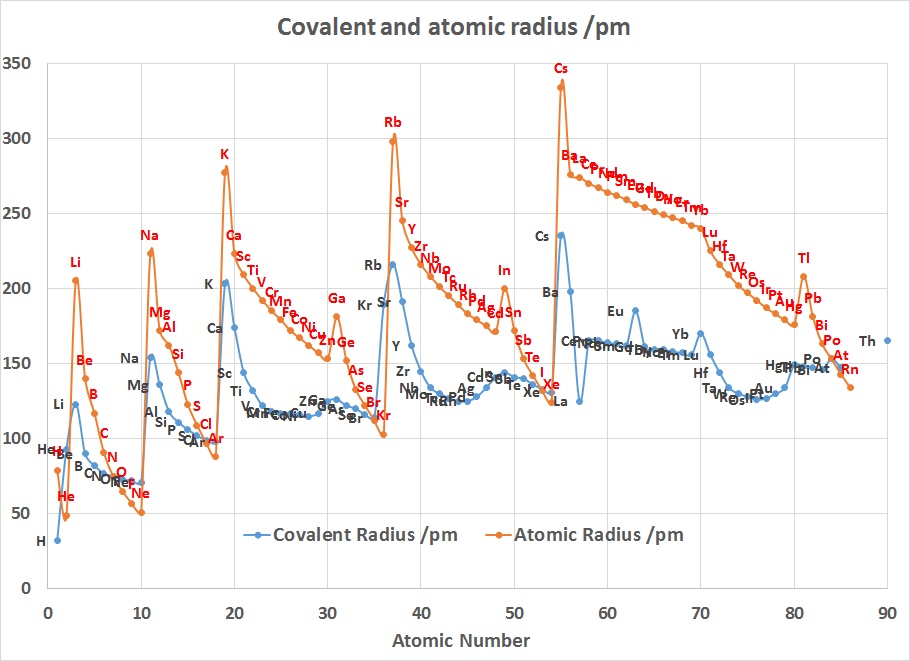
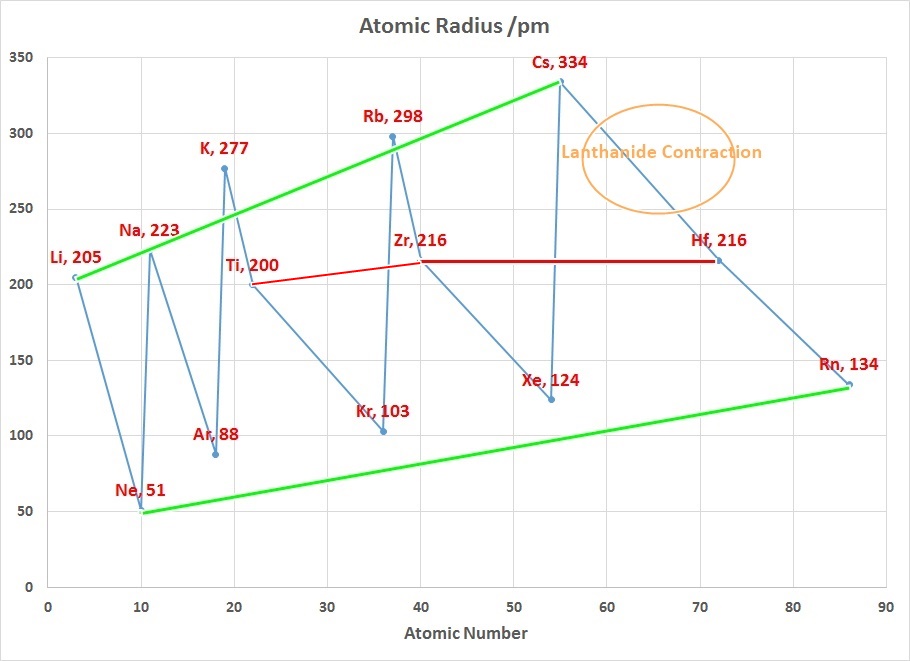
The radius increases sharply between the noble gas at the end of each period and the alkali metal at the beginning of the next period. These trends of the atomic radii (and of various other chemical and physical properties of the elements) can be explained by the electron shell theory of the atom; they provided important evidence for the development and confirmation of quantum theory. The atomic radii decrease across the Periodic Table because as the atomic number increases, the number of protons increases across the period, but the extra electrons are only added to the same quantum shell. Therefore, the effective nuclear charge towards the outermost electrons increases, drawing the outermost electrons closer. As a result, the electron cloud contracts and the atomic radii decreases.

The Lanthanide Contraction
The chart on the right above can be used to explain why Zirconium and Hafnium are two of the hardest elements in the Periodic Table to separate. In addition why the teaching of Transition Metal Chemistry is often covered in 2 courses since the properties of the first row elements are expected to be quite different to those of the second and third row.

Considering that the size of Gallium is smaller than Aluminium suggests that the 3d contraction is having an impact as well.

Ionic Radius

Although neither atoms nor ions have sharp boundaries, they are sometimes treated as if they were hard spheres with radii such that the sum of ionic radii of the cation and anion gives the distance between the ions in a crystal lattice.

Ions may be larger or smaller than the neutral atom, depending on the ion's charge. When an atom loses an electron to form a cation, the lost electron no longer contributes to shielding the other electrons from the charge of the nucleus; consequently, the other electrons are more strongly attracted to the nucleus, and the radius of the atom gets smaller. Similarly, when an electron is added to an atom, forming an anion, the added electron shields the other electrons from the nucleus, with the result that the size of the atom increases. Typical values range from 50 pm to over 220 pm.

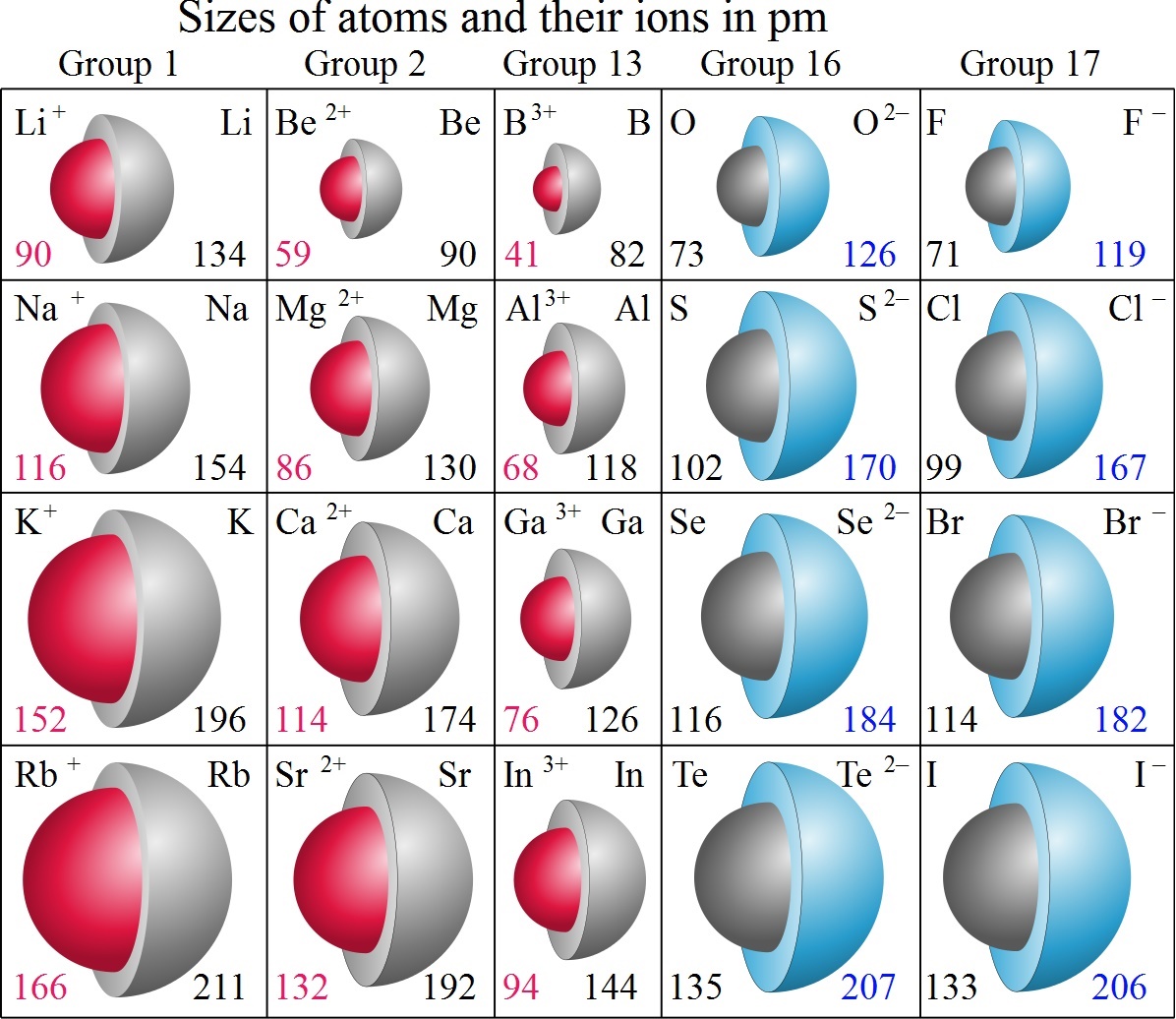
Atomic and Ionic Radius Retrieved 24 November 2014

Return to the course outline or move on to Lecture 2: Polarizing power and polarizability, Anomalous behavior of row 2 elements.

References

1. Much of the information in these course notes has been sourced from Wikipedia under the Creative Commons License.
2. 'Main Group Chemistry'- W Henderson, RSC, 2000, DOI:10.1039/9781847551283
3. 'Inorganic Chemistry' - C. Housecroft and A.G. Sharpe, Prentice Hall, 4th Ed., 2012, ISBN13: 978-0273742753, pps 24-27, 43-50, 172-176, 552-558, 299-301, 207-212