Angular Momentum II (Worksheet)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
Angular Momentum
Angular momentum is a key component in the physical descriptions of rotating systems. It is important because angular momentum, just like energy and linear momentum, must be conserved in any process. Consequently angular momentum is used to derive selection rules for spectroscopic transitions, determine which states of atoms and molecules can be affected by various perturbations, and identify possible and forbidden mechanisms in chemical reactions. Rotational angular momentum also explains the splitting of spectral lines in electric and magnetic fields and the angular distributions of gas-phase reaction products.
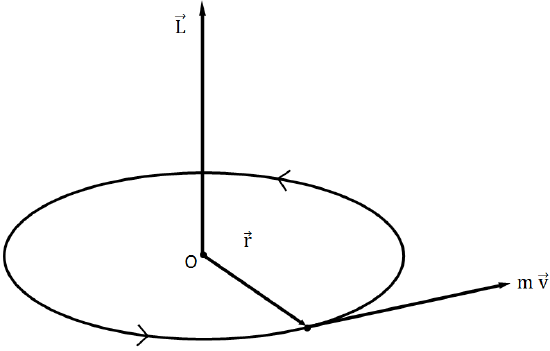
Suppose an object of mass m is revolving around a circle of radius r with speed v about an axis passing through center O as shown above. The linear momentum of the object,
p=mv
The angular momentum of an object,
→L=linear momentum×perpendicular distance from the axis of rotation
or
L=pr
Therefore,
L=mvr
This can be carried over to quantum mechanics, by reinterpreting r as the quantum position operator and p as the quantum momentum operator. ˆL is then an operator, specifically called the orbital angular momentum operator. Specifically, ˆL is a vector operator, meaning
→L=Lxi+Lyj+Lzk,
where ˆLx, ˆLy, and ˆLz are three different operators representing the projection of →L on each respective axis (i, j or k).
We can express the quantum mechanical angular momentum (in Cartesian coordinates) using operators:
- ˆLx=ˆyˆpz−ˆzˆpy=−iℏ(y∂∂z−z∂∂y)
- ˆLy=ˆzˆpx−ˆxˆpz=−iℏ(z∂∂x−x∂∂z)
- ˆLz=ˆxˆpy−ˆyˆpx=−iℏ(x∂∂y−y∂∂x)
- ˆL2=ˆL2x+ˆL2y+ˆL2z=ˆLxˆLx+ˆLyˆLy+ˆLzˆLz=−ℏ2[(y2+z2)∂2∂x2+(x2+z2)∂2∂y2+(y2+x2)∂2∂z2−2(xy∂2∂x∂y+xz∂2∂x∂z+zy∂2∂z∂y)−2(x∂∂x+y∂∂y+z∂∂z)]
Q1
What exactly does each of the the four operators above measure (more specifically, what do their eignevalues represent)?
Q2
The Cartesian components of the angular momentum do not commute with each other. This means that the components are not compatible observables. We cannot measure, for instance, Lx and Ly simultaneously, and we do not have a basis of common eigenfunctions of the two operators. Physically, this also implies that measuring one component of the angular momentum modifies the probability of finding a given result for the other two. The commutators for the angular momenta are
- [ˆLx,ˆLy]=iℏˆLz,
- [ˆLy,ˆLz]=iℏˆLx,
- [ˆLz,ˆLx]=iℏˆLy
Confirm the first commutator for ˆLx and ˆLy.
Q3
What does this tell you about the eigenfunctions for ˆLx, ˆLy, and ˆLz? (Hint: can an eigenfunction for one operator also be the eigenfunction for one of the other operators?)
Q4
Do ˆL2 and ˆLx commute? Demonstrate mathematically.
Q5
If [ˆL2,ˆLx]=0, should ˆL2 commute with ˆLy and/or ˆLz? Explain why or why not (no math needed).
Q6
If [ˆL2,ˆLx]=0, what does this tell you about the eigenfunctions for these operators and the "measurability" of their corresponding eigenvalues?
Q7
If the angular moment operators were converted to spherical coordinates, then
- ˆLx=iℏ(sinϕ∂∂θ+cotθcosϕ∂∂ϕ),
- ˆLy=−iℏ(cosϕ∂∂θ−cotθsinϕ∂∂ϕ), and
- ˆLz=−iℏ∂∂ϕ,
- ˆL2=−ℏ2[1sinθ∂∂θ(sinθ∂∂θ)+1sin2θ∂2∂ϕ2]=−ℏ2(∂2∂θ2+cotθ∂∂θ+1sin2θ∂2∂ϕ2)
Based on the simplicity of the problem, which commutator problem, [ˆL2,ˆLx]=0, [ˆL2,ˆLy]=0, or [ˆL2,ˆLz]=0 looks the easiest? Does switching to spherical coordinates change the resulting commutator relationships discussed above?


