Objectives
After completing this section, you should be able to
- discuss the formation of carbon-carbon double bonds using the concept of sp2 hybridization.
- describe the geometry of compounds containing carbon-carbon double bonds.
- compare the molecular parameters (bond lengths, strengths and angles) of a typical alkene with those of a typical alkane.
- explain why free rotation is not possible about a carbon-carbon double bond.
- explain why the lack of free rotation about a carbon-carbon double bond results in the occurrence of cis-trans isomerism in certain alkenes.
- decide whether or not cis-trans isomerism is possible for a given alkene, and where such isomerism is possible, draw the Kekulé structure of each isomer.
Key Terms
Make certain that you can define, and use in context, the key term below.
Study Notes
Your previous studies in chemistry may have prepared you to discuss the nature of a carbon-carbon double bond. If not, you should review Section 1.8 of this course before beginning the present section. It is particularly important that you make molecular models of some simple alkenes to gain insight into the geometry of these compounds.
Geometric isomerism (also known as cis-trans isomerism or E-Z isomerism) is a form of stereoisomerism. Isomers are molecules that have the same molecular formula, but have a different arrangement of the atoms in space. That excludes any different arrangements which are simply due to the molecule rotating as a whole, or rotating about particular bonds. Where the atoms making up the various isomers are joined up in a different order, this is known as structural isomerism. Structural isomerism is not a form of stereoisomerism, and is dealt with in a separate Module.
Geometric (cis / trans) isomerism
These isomers occur where you have restricted rotation somewhere in a molecule. At an introductory level in organic chemistry, examples usually just involve the carbon-carbon double bond - and that's what this page will concentrate on. Think about what happens in molecules where there is unrestricted rotation about carbon bonds - in other words where the carbon-carbon bonds are all single. The next diagram shows two possible configurations of 1,2-dichloroethane.
_and_eclipsed_(highest_energy)_conformations_of_1%252C2-dichloroethane.svg?revision=2)
These two models represent exactly the same molecule. You can get from one to the other just by twisting around the carbon-carbon single bond. These molecules are not isomers. If you draw a structural formula instead of using models, you have to bear in mind the possibility of this free rotation about single bonds. You must accept that these two structures represent the same molecule:
_and_eclipsed_(highest_energy)_conformations_of_1%252C2-dichloroethane.svg?revision=1)
But what happens if you have a carbon-carbon double bond - as in 1,2-dichloroethene?

These two molecules are not the same. The carbon-carbon double bond won't rotate and so you would have to take the models to pieces in order to convert one structure into the other one. That is a simple test for isomers. If you have to take a model to pieces to convert it into another one, then you've got isomers. If you merely have to twist it a bit, then you haven't!
Drawing structural formulae for the last pair of models gives two possible isomers:
- In one, the two chlorine atoms are locked on opposite sides of the double bond. This is known as the trans isomer. (trans : from latin meaning "across" - as in transatlantic).
- In the other, the two chlorine atoms are locked on the same side of the double bond. This is know as the cis isomer. (cis : from latin meaning "on this side")

trans-1,2-dichloroethene |

cis-1,2-dichloroethene |
The most likely example of geometric isomerism you will meet at an introductory level is but-2-ene. In one case, the CH3 groups are on opposite sides of the double bond, and in the other case they are on the same side.

trans-but-2-ene |

cis-but-2-ene |
The importance of drawing geometric isomers properly
It's very easy to miss geometric isomers in exams if you take short-cuts in drawing the structural formulae. For example, it is very tempting to draw but-2-ene as
CH3CH=CHCH3
If you write it like this, you will almost certainly miss the fact that there are geometric isomers. If there is even the slightest hint in a question that isomers might be involved, always draw compounds containing carbon-carbon double bonds showing the correct bond angles (120°) around the carbon atoms at the ends of the bond. In other words, use the format shown in the last diagrams above.
How to recognize the possibility of geometric isomerism
You obviously need to have restricted rotation somewhere in the molecule. Compounds containing a carbon-carbon double bond have this restricted rotation. (Other sorts of compounds may have restricted rotation as well, but we are concentrating on the case you are most likely to meet when you first come across geometric isomers.) If you have a carbon-carbon double bond, you need to think carefully about the possibility of geometric isomers.
What needs to be attached to the carbon-carbon double bond?
Think about this case:

Although we've swapped the right-hand groups around, these are still the same molecule. To get from one to the other, all you would have to do is to turn the whole model over. You won't have geometric isomers if there are two groups the same on one end of the bond - in this case, the two pink groups on the left-hand end. So there must be two different groups on the left-hand carbon and two different groups on the right-hand one. The cases we've been exploring earlier are like this:

But you could make things even more different and still have geometric isomers:

Here, the blue and green groups are either on the same side of the bond or the opposite side. Or you could go the whole hog and make everything different. You still get geometric isomers, but by now the words cis and trans are meaningless. This is where the more sophisticated E-Z notation comes in.
-_and_(E)-2-bromo-1-chloro-1-iodoethene.svg?revision=1)
Rigidity of C=C Bonds
As discussed in Section 1.8 the double bond in the molecule ethene (H2C=CH2) is created by the overlap of two different sets of orbitals. The C-C σ bond is formed when an sp2 orbital from each carbon atom overlaps end to end. Also, the C-C pi bond is created by the side-to-side overlap of a pz orbital from each carbon atom.

Because they are the result of side-by-side overlap (rather then end-to-end overlap like a sigma bond), pi bonds are not free to rotate. If rotation about this bond were to occur, it would involve disrupting the side-by-side overlap between the two 2pz orbitals that make up the pi bond. If free rotation were to occur the p-orbitals would have to go through a phase where they are 90° from each other, which would break the pi bond because there would be no overlap. Since the pi bond is essential to the structure of ethene it must not break, so there can be no free rotation about the carbon-carbon sigma bond. The presence of the pi bond thus ‘locks’ the six atoms of ethene into the same plane.
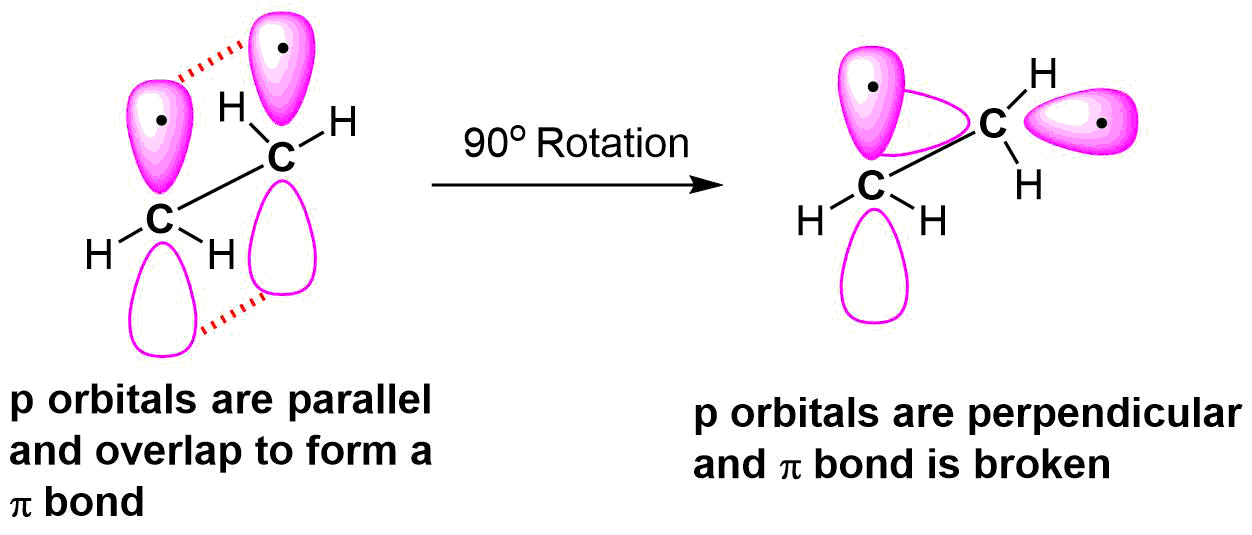
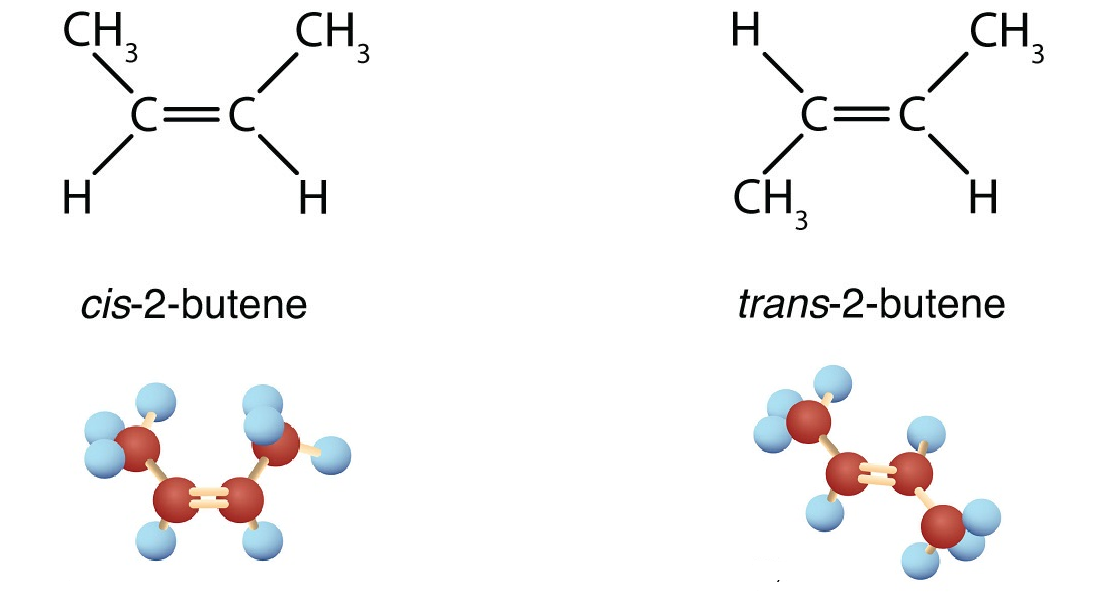
Restricted rotation about the double bond means that the relative positions of substituent groups above or below the double bond become significant. This leads to a special kind of isomerism in double bonds. Consider the alkene with the condensed structural formula CH3CH=CHCH3. We could name it 2-butene, but there are actually two such compounds due to this isomerism. The isomer in which the two methyl (CH3) groups lie on the same side of the molecule is called the cis isomer (Latin cis, meaning “on this side”) and is named cis-2-butene. The isomer with the two (CH3) groups on opposite sides of the molecule is the trans isomer (Latin trans, meaning “across”) and is named trans-2-butene. These two compounds are cis-trans isomers (or geometric isomers), compounds that have different configurations (groups permanently in different places in space) because of the presence of a rigid structure in their molecule. In general these isomers have different physical, chemical, and physiological properties.
It is important to note that the presence of a double bond does not necessarily lead to cis-trans isomerism. Being able to tell if a double bond has the possibility of isomerism is a very important skill. Cis-trans can occur whenever both double-bond carbons are directly attached to a carbon and a hydrogen. In this case, interchanging the substituents on one of the double-bond carbons creates a different isomer.

If one of the double-bond carbons of an alkene is attached to two identical groups, cis-trans isomerism is not possible. Here, interchanging the substituents on one of the double-bond carbons forms an identical molecule.

Worked Example \(\PageIndex{1}\)
Are the following molecules cis-trans isomers?

- Answer
-
Although the two molecules are seemingly different propenes, these two structures are not really different from each other. Because the one of the double-bond carbons is attached to two identical groups (hydrogens) it is incapable of forming cis-trans isomers. The interchange of two substituents seen here does not create a new isomer. If either molecule were flipped over top to bottom, the two would you would look identical.
Exercise \(\PageIndex{1}\)
Classify each compound as a cis isomer, a trans isomer, or neither.

- Answer
-
a) trans isomer
b) neither
c) cis isomer
d) cis isomer
Exercise \(\PageIndex{2}\)
Which of the following compounds could exist as cis/trans isomers? Draw (& label) both of the isomers for the ones that can.
- CH3CH=CHCH3
- (CH3)2C=CHCH3
- H2C=CHCH3
- CH3CH2CH=CHBr
- Answer
-

Exercise \(\PageIndex{3}\)
Draw (& label) the cis and trans isomer for each of the following compound names. If no cis/trans isomerism is possible, write none.
- 3-hexene
- 1-hexene
- 4-methylpent-2-ene (4-methyl-2-pentene)
- 1,1-dibromobut-2-ene (1,1-dibromo-2-butene)
- Answer
-

Exercise \(\PageIndex{4}\)
Name the following compounds using cis/trans nomenclature

- Answer
-
a) trans-4-methylhex-2-ene (trans-4-methyl-2-hexene)
b) cis-2,5-dibromohex-3-ene (cis-2,5-dibromo-3-hexene)




