The Electrochemical Series
- Page ID
- 3846
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Arranging REDOX equilibria in order of their E° values
The electrochemical series is built up by arranging various redox equilibria in order of their standard electrode potentials (redox potentials). The most negative E° values are placed at the top of the electrochemical series, and the most positive at the bottom. For this introductory look at the electrochemical series we are going to list the sort of metal / metal ion equilibria that we looked at on the previous page (plus the hydrogen equilibrium) in order of their E° values.
The electrochemical series
| equilibrium | E° (volts) |
|---|---|
| \(\ce{Li+(aq) + e^- <=> Li(s)}\) | -3.03 |
| \(\ce{K+(aq) + e^- <=> K(s)} \) | -2.92 |
| \(\ce{Ca^2+(aq) +2e^- <=> Ca(s)} \) | -2.87 |
| \(\ce{Na+(aq) + e^- <=> Na(s)} \) | -2.71 |
| \(\ce{Mg^2+(aq) + 2e^- <=> Mg(s)} \) | -2.37 |
| \(\ce{Al^3+(aq) + 3e^- <=> Al(s)} \) | -1.66 |
| \(\ce{Zn^2+(aq) + 2e^- <=> Zn(s)} \) | -0.76 |
| \(\ce{Fe^2+(aq) + 2e^- <=> Fe(s)} \) | -0.44 |
| \(\ce{Pb^2+(aq) + 2e^- <=> Pb(s)} \) | -0.13 |
| \(\ce{2H+(aq) + 2e^- <=> H2(g)} \) | 0 |
| \(\ce{Cu^2+(aq) + 2e^- <=> Cu(s)} \) | +0.34 |
| \(\ce{Ag+(aq) + e^- <=> Ag(s)} \) | +0.80 |
| \(\ce{Au^3+ + 3e^- <=> Au(s)} \) | +1.50 |
A note on the hydrogen value
Remember that each E° value shows whether the position of the equilibrium lies to the left or right of the hydrogen equilibrium. That difference in the positions of equilibrium causes the number of electrons which build up on the metal electrode and the platinum of the hydrogen electrode to be different. That produces a potential difference which is measured as a voltage. Obviously if you connect one standard hydrogen electrode to another one, there will be no difference whatsoever between the positions of the two equilibria. The number of electrons built up on each electrode will be identical and so there will be a potential difference of zero between them.
Remember that in terms of electrons:
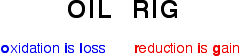
Now apply this to one of the redox equilibria:
\[ \ce{Mg^{2+} (aq) + 2e^- <=> Mg (s)}\]
When solid magnesium forms its ions, it loses electrons. The magnesium is being oxidized. Taking another example . . .
\[ \ce{Cu^{2+} (aq) + 2e^- <=> Cu(s)}\]
When the copper(II) ions gain electrons to form copper, they are being reduced.
Reducing agents and oxidizing agents
A reducing agent reduces something else. That must mean that it gives electrons to it, e.g. magnesium is good at giving away electrons to form its ions and must be a good reducing agent.
An oxidizing agent oxidizes something else. That must mean that it takes electrons from it, e.g. copper doesn't form its ions very readily, and its ions easily pick up electrons from somewhere to revert to metallic copper. Copper(II) ions must be good oxidizing agents.
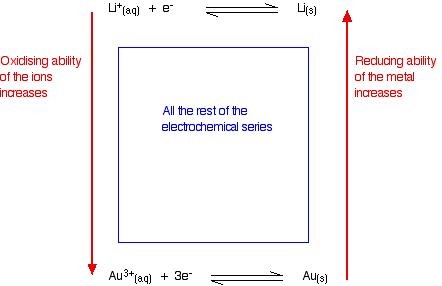
Summarizing this on the electrochemical series
- Metals at the top of the series are good at giving away electrons. They are good reducing agents. The reducing ability of the metal increases as you go up the series.
- Metal ions at the bottom of the series are good at picking up electrons. They are good oxidizing agents. The oxidizing ability of the metal ions increases as you go down the series.
Judging the oxidizing or reducing ability from E° values
- The more negative the E° value, the more the position of equilibrium lies to the left - the more readily the metal loses electrons. The more negative the value, the stronger reducing agent the metal is.
- The more positive the E° value, the more the position of equilibrium lies to the right - the less readily the metal loses electrons, and the more readily its ions pick them up again. The more positive the value, the stronger oxidizing agent the metal ion is.
Contributors
Jim Clark (Chemguide.co.uk)