Unit 11: Nuclear Chemistry
- Page ID
- 93401
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Introduction
Nuclear reactors were first created in 1940’s. Today, newer and safer models have been developed, but the risks, cost, and management of the current power stations, has halted the production of new plants in the United States. Yet, nearly 20% of the countries electrical energy is supplied by the current plants and some of them are reaching the end of their projected lifetime. How we deal with nuclear power is going to be a major issue (as is oil and gas extraction and production) in the foreseeable future? Like the study of all sciences, understanding the basics science of a process or product helps us to make the best decisions personally and for the community. With nuclear chemistry the need for understanding the nature of radiation and half-lives of isotopes is clear and direct.
The Structure of the Atom
The atom is composed of a nucleus surrounded by an electron cloud. The electron cloud contains all the electrons. Each electron travels within the cloud with their own specific energy that limits their travels to a specific orbital and specific spin. It is the pattern of orbitals and the energies of the valence electrons that governs the chemistry of substances. The nucleus contains the particles with mass, the proton and neutron. Each atoms contains a set number of protons that is unique for each element. Each element has different isotopes (although, for example, fluorine has only one stable isotope in nature) where each isotope contains varying number of neutrons and the same number of protons. Some isotopes are stable and some isotopes are unstable. Nuclear chemistry is about the changes that occur in an unstable isotope.
The Structure of the Nucleus
The protons and neutrons, which are the particles with mass, crowd together in the center of the nucleus, occupying only 1/10,000th of the volume. This is like taking all the people who could fill a football stadium, collapsing them into a space the size of a large walnut, while leaving a bag of peanuts for each person behind to represent the electrons. Moreover, the protons and neutrons are actually formed from smaller particles called quarks. Quarks have been proposed and discovered only in the last half century. In 1964, quarks where predicted, in 1968 quarks where observed, and by 1977 five quarks where identified. The final “top” quark was found only in 1995, and by the early theory of 1964 was part of the conventional understanding of the structure of the nucleus.
Quarks
There are six flavors of quarks: up, down, strange, charmed, bottom, and top. Protons and neutrons are each made up of three up and down quarks held together by particles called gluons. A proton contains two up and one down quark, and a neutron contains two down and one up quark. Protons and neutrons are referred to as fundamental particles when discussing the number of particles in a nucleus, but they are called baryons when they are part of a discussion of quarks. Quarks and leptons, which is a class of particles that includes electrons, are called elementary particles, because they are the smallest particles to make up all matter.

Illustration of Quarks in a Proton. (like all particles quarks are in motion) http://commons.wikimedia.org/wiki/File:Quark_wiki.jpg
Charge
Charge is a fundamental property of protons, electrons, and quarks. The charge of a proton is positive, +1, and the charge of an electron is negative, –1. The charge of quarks is +⅔ for up quarks and -⅓ for down quarks (which is consistent with a neutron being neutral, since it contains two down quarks and one up quark). Charge exerts a force over distance between particles. Like charges repel, or push each other, thus two protons or two electrons will repel each other. Unlike charges attract, or pull each other, thus protons are attracted to electrons. The force of repulsion and attraction depends on distance, and, like gravity, it becomes exponentially weaker as the distance between two charges increases. This exponential decrease can be graphed using Coulomb’s Law: \(F\;=\;k\frac{q_{1}q_{2}}{r^{2}}\), where F is force, k is a constant, q is the amount of charge for two points of charge 1 and 2, and r is the distance between the two charges. When the charges are close together like in the nucleus the force is incredibly strong, but as the particles move farther apart the force is reduced significantly (see the graph)
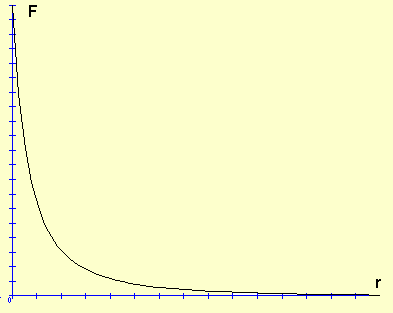
Force,F, vs. distance,r for two charges q1 and q2 http://commons.wikimedia.org/wiki/File:Inversa.png
Strong Force
If like charges repel then pushing the protons into such a small space as the nucleus, then the forces of repulsion must be very strong. So the force that stabilizes the nucleus and holds it together must be extremely strong; consequently the binding force in the nucleus is called the strong force. In fact, while the electrical force of charge is much greater than the force of gravity, the, which binds the protons and neutrons in the nucleus, is strongest of all known forces. In a stable isotope the strong force overcomes the repulsive forces between protons. In an unstable nucleus the strong force is unable to hold the nucleus together. Sometime the unstable nucleus flies apart in microseconds and sometimes it takes millions of years for the unstable nucleus to fall apart. A graph of the number of neutrons versus the number of protons shows a band of stability for the stable isotopes of the different elements. When the number of neutrons is higher or lower than these stable isotopes the isotope is unstable. Stable isotopes have a ratio of neutrons to protons near 1:1 when the atomic mass is low and when the isotope has a high atomic mass the ratio is near 1.5:1.
The strong force can act on protons and neutrons only within the limited confines of the nucleus. As the nucleons spread apart the strong force drops off rapidly so that repulsive force between protons soon overcomes the binding energy of the strong force.

Band of Stability, the black line represents the small number of stable isotopes. http://commons.wikimedia.org/wiki/File:Table_isotopes_en.svg
Unstable Isotopes and Radioactivity
An unstable isotope is destine to change, the strong force cannot hold the nucleus together. There are either too few neutrons, like helium-3 or 3He, or there are too many neutrons, like carbon-14, 14C. When the unstable nucleus breaks apart particles and energy is released. The particles themselves have high energy and can cause changes to the matter that they encounter. These high energy particles are called radioactivity. Radioactivity can cause other atoms to become unstable and radioactive, it can damage cells by altering molecules, it heats up matter when the energy is absorbed, and it can lead to other changes to matter.
Radioactive Elements Stable Negligible radioactivity Dangerous radioactivity http://commons.wikimedia.org/wiki/File:Periodic_Table_Radioactivity.svg
Radioactivity is a natural process and it is present in the foods we eat, the buildings we work in, and in the air around us. While radiation is something to be concerned with, just like worrying about getting too much sun when you are tanning, natural radiation is low enough for our bodies to handle. But when natural sources of radiation are concentrated then either by a manufacturing process or by a natural process then there is a real concern of skin and internal organ damage like a bad sun burn, or that radiation can lead to cancerous growth when the instruction code of DNA is altered. Radon gas is emitted from several types of rock, especially in the northeast. While this release of gas is part of the natural background radiation, it can be concentrated in basements that have good insulation. The concentrated gas is a real danger and there are a wide selection of kits and companies to check for excess radon in rooms. When uranium products are purified, they can be radioactive. A very nice orange color formed from uranium oxide was used in pottery, until it was decided that it was too high a concentration of uranium and represented a radiation risk. And since energy is released as light from radium, a radium paint was used on watch dials (long before digital watches with LED lights) so that the time could be seen in the dark. However, the workers painting the watch dials developed cancers of the mouth from sharpening the point of their brushes in their mouth.
We still use radioactive sources even in medicine. An unstable isotope of cesium, cesium-137 or 137Cs, is used in cancer therapies, and iodine-131, 131I, is used to treat thyroid cancer. Medical imaging techniques use fluorine-18, 18F, for PET scans. Technium-99, 99Tc, is detected with a gamma camera after it is injected into patients where it is absorbed into bones; thus allowing doctors to find bone cancers. Americium-241 is used in smoke detectors. Cobalt-60 is used to find flaws in metallic products, and it is used to kill bacteria in food products without creating radioactive food. Carbon-14 and potassium-40 are used for radioactive dating, that allows use to estimate the time for the death of a living organism and the time for the formation of a rock respectively. There are many more uses of radioactive isotopes, radionuclides. The EPA has a nice listing of radioactive isotopes, radionuclides, that can be researched at http://www.epa.gov/rpdweb00/radionuclides/index.html, and the Nuclear Regulatory Commission, NRC, has information on radionuclides, including The Regulation and Use of Radioisotopes in Today's World, found at the electronic reading room of the NRC, http://www.nrc.gov/reading-rm/doc-co...s/fact-sheets/ .
Types of Radioactivity
When an unstable isotope changes by breaking into smaller nuclei, by changing neutrons to protons, by fusing together, by losing excess energy, or other change, it releases particles or energy which is called radioactivity. There are many types of radioactivity but there are three major types. They are listed a, b, and c but from the greek alphabet: α, alpha; β, beta; and γ, gamma. These particles are emitted by radioactive isotopes as the isotopes attempt to form more stable structures. An α-emission, or α-decay emits a helium nucleus, 42He, as the nucleus emits several particles to form a more stable structure. A β–emission, or β-decay, releases an energetic electron that is formed as a neutron forms a proton in order to balance the number of protons and neutrons to a more stable ratio. Finally, a γ-emission, or γ-ray, is a very high energy electromagnetic wave (like super high energy light) that easily passes through much material but imparts great energy and results in large change when it is absorbed. Each type of decay has a certain penetrating power, or the amount of material that can be used to safely protect you from the radiation emitted from an unstable nuclei. The large, low energy alpha particle, α, is stopped by cardboard or canvas. The beta particle, β–, is stopped by metal sheets, and gamma rays, γ, are difficult to stop even with feet of concrete or inches of lead are needed to absorb the energy (see image).
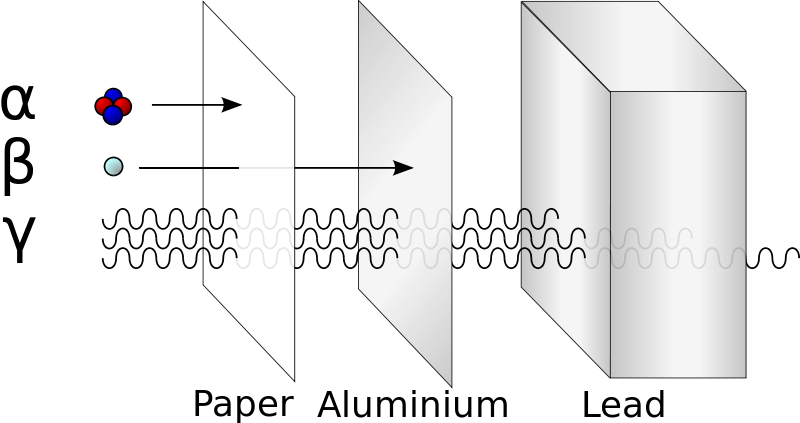
http://en.wikipedia.org/wiki/File:Alfa_beta_gamma_radiation_penetration.svg
Because of their weak penetrating power, alpha radiation only causes minor damage in biological systems. So while prolonged exposure can cause burns and ingestion can focus damage on sensitive organs, sources of alpha radiation are typically safe to use. Beta particles which can more easily burn the skin and can reach internal organs, does require more strict regulation and monitoring, but methods of protecting workers and living organisms are relatively easy to put in place. Gamma radiation and neutron emission, which is another type of radiation of concern, are very dangerous and strict regulations that monitor containment and use of isotopes producing these types of radiation are necessary. The building, maintenance, and monitoring of nuclear power plants is very costly and severely limits the economic benefits of nuclear power.
| Particle | Symbol | Composition | Penetrating Power |
|---|---|---|---|
| alpha particle | \(\alpha,\; ^{4}_{2}{He^{2+}},\; He,\; He^{2+}\) | two protons & two neutrons | stopped by thick paper or cloth |
| beta particle | \(\beta,\; \beta^{-},\;e^{-},\; ^{0}_{-1}{e}\) | a high energy electron | stopped by thick sheets of metal or plastic |
| gamma ray | \(\gamma,\;^{0}_{0}{\gamma}\) | Highest type of electromagnetic energy, it is a wave of high energy light | stopped by thick lead walls, or feet of concrete or rock. |
Fission
The nuclear reaction we are most familiar with is the explosions of atomic and hydrogen bombs caught on black and white film by the US defense department, and the reactions that must be powering nuclear power plants. Atomic bombs and nuclear power plants use the same type of nuclear reaction: fission of purified uranium-235. Fission is the nuclear reaction that results in the division of an unstable nucleus. Fission occurs naturally in large unstable nuclei like uranium-235, polonium-210, and plutonium-239. The fission of uranium-235 is accelerated with the absorption of a neutron in a nuclear reactor or atomic bomb. neutron fission with energy and radiation of three neutrons
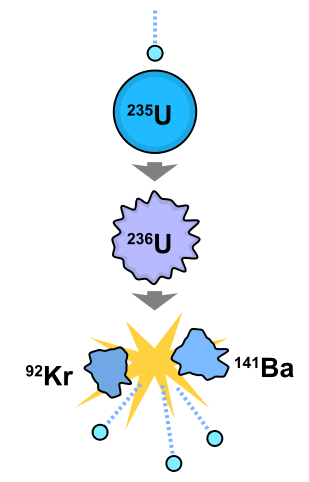
Fission: the splitting of a atomic nucleus http://en.wikipedia.org/wiki/File:Nuclear_fission.svg
Fusion
Fusion is the energy source of the sun. The most abundant element in the universe, hydrogen, is pressed together by the huge gravitational forces of the sun until they react to form a helium nucleus (the hydrogens involved in the fusion reaction are tritium that has two neutrons and deuterium which has one neutron and not the common hydrogen atom without any neutrons). Fusion is the nuclear reaction in a hydrogen bomb. It is also being studied actively as a new source of energy in power plants. Currently, the researchers have been able to contain a fusion reaction using magnets and lasers, and they have created more energy than they used to start the reaction, but any commercially viable fusion power plant is decades away.
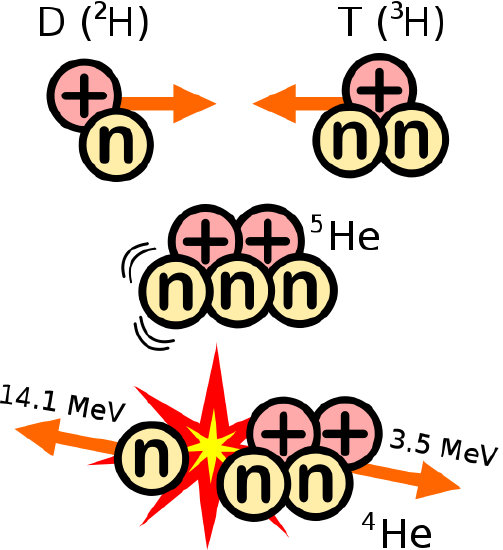
Fusion: combining atomic nuclei D is deuterium, and T is tritium https://commons.wikimedia.org/wiki/File:D-T_fusion.svg
Writing Nuclear Reactions
Nuclear reactions obey the law of conservation of mass where the mass of the reacting atoms as measured by the number of protons and neutrons in the nuclei is the same as the mass of the reactants. The charge of the reaction is also conserved, just like ratio of cations and anions in ionic compounds, which is shown by indicating the number of protons and using a -1 to represent beta particles. Besides fission and fusion reactions, nuclear reactions can be classified as either emission, where atomic particles are expelled, or capture, where atomic particles are absorbed. Each isotope is written with the atomic symbol and the atomic mass in the upper left side of the symbol. Often the atomic number is added to the lower left side of the symbol to represent the charge (and beta particles have a -1 in this location).
| alpha emission: | \(^{235}_{92}{U}\;\rightarrow\;^{234}_{90}Th + ^{4}_{2}He\) | α-decay: the product is a He nucleus |
| beta emission: | \(^{14}_{6}{C}\;\rightarrow^{14}_{7}{N} + ^{0}_{-1}{e}\) |
β-decay: the product is a high energy electron e- |
| positron emission: | \(^{49}_{24}{Cr}\;\rightarrow\;^{49}_{23}{V}\;+\;^{0}_{+1}{e}\) | a positron is a positive electron, e+ |
| electron capture: | \(^{81}_{36}{Kr}\;+\;^{0}_{-1}{e}\;\rightarrow^{81}_{36}{Br}\) | a capture adds a particle, like the beta particle, e- |
| neutron capure: | \(^{81}_{7}{N}\;+\;^{1}_{0}{n}\;\rightarrow\;^{12}_{6}{C}\;+\;^{1}_{1}{H}\) |
\(^{1}_{0}{n}\) is a neutron and \(^{1}_{1}{H}\) is a proton |
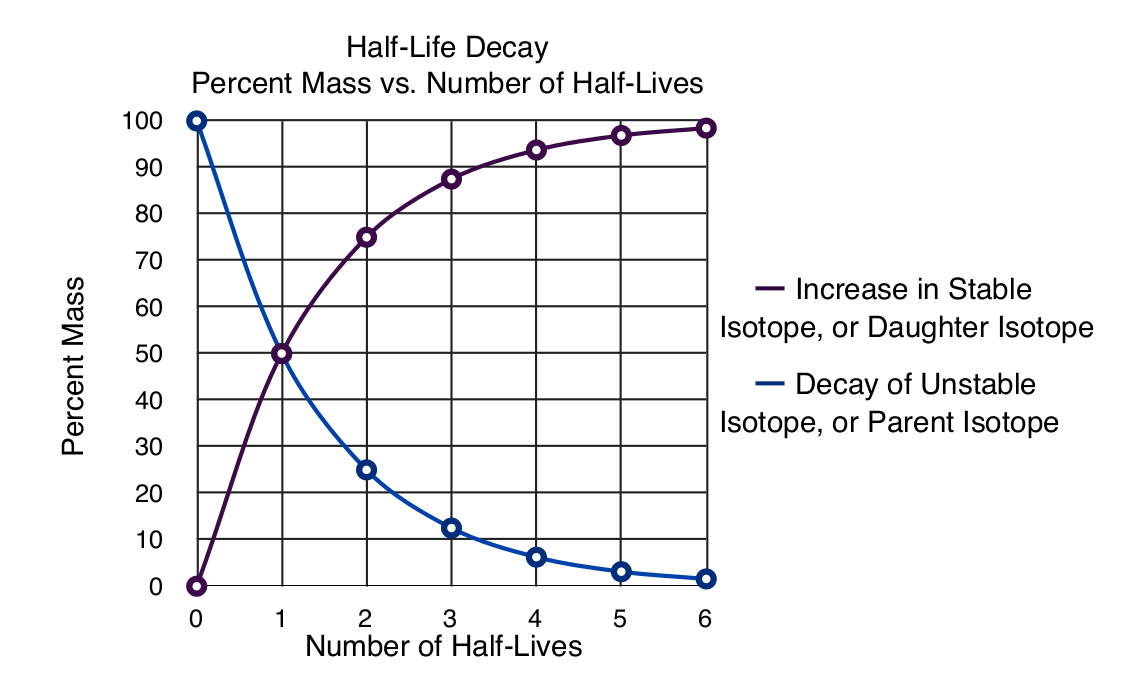
Half-Life
Radioactive decay of an unstable isotope takes place so that the same fraction of isotopes decay in a specific amount of time regardless of the amount of material. Half-life is the amount of time it takes for 1/2 of the unstable parent isotope to decay to the new isotope called the daughter isotope. The half-life can take seconds or millions of years depending on the isotope. For example, potassium-40 has a half-life of 1.25 billions years, carbon 14 has a half-life of 5700 years, radon-222 has a half-life of 4.8 minutes, and meitnerium-276 has a half-life of 40 seconds. Moreover, regardless of whether the half-life is measured from the beginning amount of isotope or it is measured after barely any unstable isotope remains after millions of years, the half-life for the decay of an unstable isotope is constant.
The graph below shows the percent change in the amount of any isotope after a certain number of half-lives have passed. The change is always 1/2 the original amount no matter how small the remaining unstable isotope remains.
Recall that the unstable isotope is changing in to another isotope, often one that is table, so the mass of the sample does not necessarily change unless the radiation emitted by the decay are alpha particles.
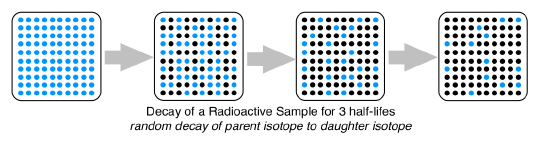
The decay that occurs in a radioactive isotope is always random. If you were to pick any atom in a sample of the unstable isotope, their is no way to tell if it will decay in the first half-life or the 10th half-life. In this picture the decay is random, so there is no part of the sample that will become less radioactive than any other portion.
Calculating the Amount of Radioactive Isotope Remaining
Because of the constant rate of decay, it is possible to determine how long a substance has been decaying after it has been created. When a living organism dies, the cellular processes that replace dying cells stop. This means that the carbon in the cells has stopped changing and the greatest amount of carbon-14, the most common radioactive isotope of carbon, is present in the organism. From this point onward carbon-14 will decay to stable nitrogen-14. By examining the ratio of carbon-14 to nitrogen-14, it is possible to determine how long the organism has been dead. This method of using radioactive isotopes to date the age of a sample is called radioactive dating. Dating methods are correlated to other methods like tree rings and geological strata, to make sure they are accurate, and use a variety of isotopes. Besides carbon-14 which is useful only for living organisms and for periods of time no longer than 50,000 years, geologists use potassium-40 and uranium-238 to date long geologic periods like the age of the earth and rocks from prehistoric periods.
To find out how much radioactive isotope remains in a sample one can use the formula:
\(N_{t}\;=\;N{o} \cdot \frac{1}{2}^{(t/{t\frac{1}{2}})}\)
where Nt is the amount of sample remaining after time t, No is the beginning amount of sample, \((t/{t\frac{1}{2}})\) is the fraction of t,time of decay, divided by the half-life, \(t\frac{1}{2}\). However, if the time that the sample has decayed is a whole number ratio of the half-life, then the amount of radioactive isotope remaining can be found by multiplying the original sample by 1/2 for each half–life that has passed.
Example \(\PageIndex{1}\):
Q: The half-life of carbon-14, C-14, is 5730 years. For a 5 gram sample of C-14 how much of the radioactive isotope will remain after 17160 years?
A: 17160 / 5730 = 3 {17160 is 3 half-lives} ⇒ 5 g•1⁄2•1⁄2•1⁄2 = 0.625g {Multiply the starting amount by 1/2 for each half-life that has passed}
Example \(\PageIndex{2}\):
Q: A 4.0 g sample of uranium-234 has been discovered that is said to be 640,000 years old. If the half-life is 80,000 years then how much of the unstable isotope remains?
A: 400,000 / 80,000 = 5 half-lives ⇒ 4 • 1⁄2•1⁄2•1⁄2•1⁄2•1⁄2 = 4 • (1⁄2) 5 = 0.125 g U-234 remains
E=mc2
Einstein’s famous equation has been so quoted that it is the equation that represents science. Einstein developed his ideas of special relativity which discussed masses and their peculiar properties at velocities near the speed of light. In doing so he concluded that mass and energy are “different manifestations” of the same thing, and related by the equation E=mc2 , where E is energy, m is mass and c is the speed of light, 3.00 X 108 m/s. Since c2 is 9.00 X 1016 m/s, then even a small conversion of mass to energy results in a large amount of energy. Nuclear reactions have been shown that the reactants have a slightly greater mass than the products. Einstein’s equation shows that the energy from the loss of mass is enormous and even small changes in mass will be able to generate energy that is useful for industrial processes. No chemical reaction can match the energy released from nuclear reactions. So a bomb with TNT or C-4 will never match the power of a bomb using nuclear reactions (unless the mass of the conventional bomb is very large and the mass of the nuclear reaction is minute). Likewise the energy generated in the burning of oil, coal, or gas will not match the power of energy generated in fusion and fission reactions.
Contributors
Kenneth Pringle and Curriki. This content is licensed under a Creative Commons Attribution Share-Alike 3.0 License.


