2.1: Early Chemical Discoveries and Atomic Theory
- Page ID
- 19686
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Learning Objectives of this Module are:
- Explain how all matter is composed of atoms.
- Describe the modern atomic theory.
Take some aluminum foil. Cut it in half. Now there are two smaller pieces of aluminum foil. Cut one of the pieces in half again. Cut one of those smaller pieces in half again. Continue cutting, making smaller and smaller pieces of aluminum foil.
It should be obvious that the pieces are still aluminum foil; they are just becoming smaller and smaller. But how far can this exercise be taken, at least in theory? Can one continue cutting the aluminum foil into halves forever, making smaller and smaller pieces? Or is there some limit, some absolute smallest piece of aluminum foil? (Thought experiments like this—and the conclusions based on them—were debated as far back as the fifth century BC.)
The modern atomic theory, proposed about 1803 by the English chemist John Dalton (Figure 2.2), is a fundamental concept that states that all elements are composed of atoms. Previously, an atom was defined as the smallest part of an element that maintains the identity of that element. Individual atoms are extremely small; even the largest atom has an approximate diameter of only 5.4 × 10−10 m. With that size, it takes over 18 million of these atoms, lined up side by side, to equal the width of the human pinkie (about 1 cm).

Figure 2.2 John Dalton was an English scientist who enunciated the modern atomic theory.
John Dalton (1766-1844) is the scientist credited for proposing the atomic theory. The theory explains several concepts that are relevant in the observable world: the composition of a pure gold necklace, what makes the pure gold necklace different than a pure silver necklace, and what occurs when pure gold is mixed with pure copper. Before discussing the atomic theory, this article explains the theories that Dalton used as a basis for his theory: the law of conservation of mass and the law of constant composition.
Law of Conservation of Mass: (1766-1844)
The law of conservation of mass states that the total mass present before a chemical reaction is the same as the total mass present after the chemical reaction; in other words, mass is conserved. The law of conservation of mass was formulated by Antoine Lavoisier (1743-1794) as a result of his combustion experiment, in which he observed that the mass of his original substance—a glass vessel, tin, and air—was equal to the mass of the produced substance—the glass vessel, “tin calx”, and the remaining air.
Historically, this was a difficult concept for scientists to grasp. If this law was true, then how could a large piece of wood be reduced to a small pile of ashes? The wood clearly has a greater mass than the ashes. From this observation scientists concluded that mass had been lost. However, Figure 1 shows that the burning of word does follow the law of conservation of mass. Scientists did not account for the gases that play a critical role in this reaction.
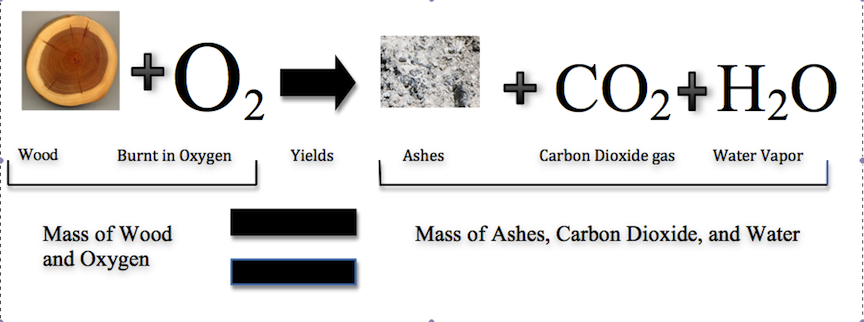
Figure 1: Image of the wood courtesy of Ehamberg and Stannered on Wikimedia Commons,
available under Creative Commons Attribution 2.5 Generic license. Image of ashes courtesy of Walter Siegmund under the creative
commons-share alike 3.0 unported license. Figure 1 as a whole constructed by Jessica Thornton using Microsoft Word and Preview (UCD).
Law of Constant Composition
Joseph Proust (1754-1826) formulated the law of constant composition (also called the law of definite proportions). This law states that if a compound is broken down into its constituent elements, the masses of the constituents will always have the same proportions, regardless of the quantity or source of the original substance. Joseph Proust based this law primarily on his experiments with basic copper carbonate. The illustration below depicts this law; 31 grams of H2O and 8 grams of H2O are made up of the same percent of hydrogen and oxygen.

Figure 2: Constructed by Jessica Thornton (UCD)
Dalton's Atomic Theory
1. Each chemical element is composed of extremely small particles that are indivisible and cannot be seen by the naked eye, called atoms. Atoms can neither be created nor destroyed. Pictured below is a helium atom. The purple and red dots represent the neutrons and protons in the nucleus. The black area around the nucleus represent the electron cloud. The following sections discuss this further.
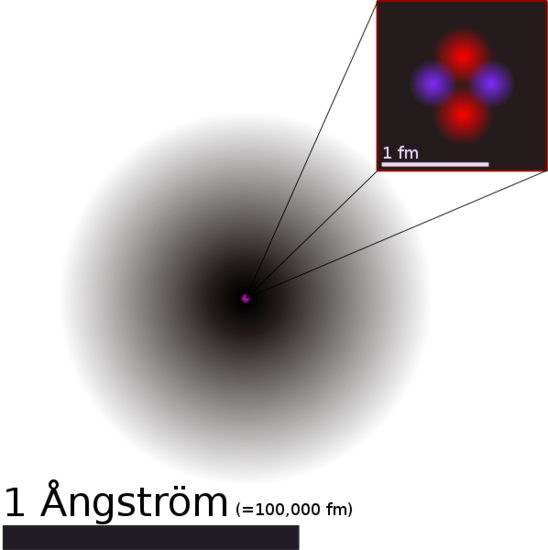
Figure 3: Courtesy of Yzmo on Wikimedia commons, available under Creative Commons-Share Alike 3.0 Unported
2. All atoms of an element are alike in mass and other properties, but the atoms of one element differ from those of all other elements. For example, gold and silver have different atomic masses and different properties.


Gold Silver
Atomic Mass: 196.97 Atomic Mass: 107.87
Figure 4 (Gold): Courtesy of Chris Ralph that released this image into the public domain.
Figure 5 (silver): Courtesy of http://resourcescommittee.house.gov/subcommittees/emr/usgsweb/photogallery/
3. For each compound, different elements combine in a simple numerical ratio. The illustration below describes this rule. The second equation for the reaction is incorrect because half of an atom does not exist.
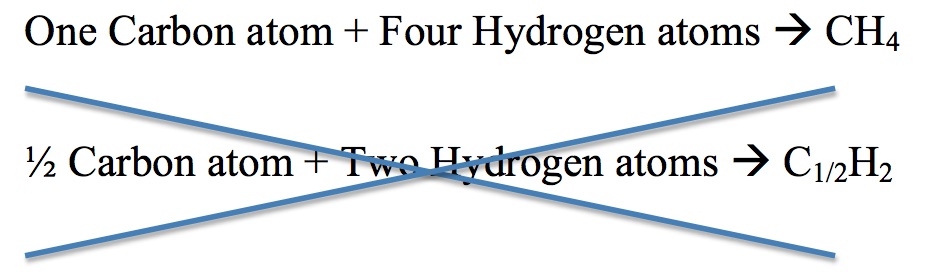
Figure 6: Created by Jessica Thornton
Atomic theory can be used to answers the questions presented above. A pure gold necklace is made up of gold atoms. A pure gold necklace and a pure silver necklace are different because they have different atoms. Pure gold mixed with pure copper forms rose gold. The gold and copper atoms combine in a simple numerical ratio.
Dalton's theory has not proven to be correct under all circumstances. The first rule was proven incorrect when scientists divided atoms in a process called nuclear fission. The second rule was proven incorrect by the discovery that not all atoms of the same element have the same mass; there are different isotopes. However, these failures do not justify discarding the atomic theory. It correctly explains the law of conservation of mass: if atoms of an element are indestructible, then the same atom must be present after a chemical reaction as before and, and the mass must constant. Dalton’s atomic theory also explains the law of constant composition: if all the atoms of an element are alike in mass and if atoms unite in fixed numerical ratios, the percent composition of a compound must have a unique value without regards to the sample analyzed. The atomic theory led to the creation of the law of multiple proportions.
Law of Multiple Proportions
The law of multiple proportions states that if two elements form more than one compound between them, the masses of one element combined with a fixed mass of the second element form in ratios of small integers. The illustration of the third rule of the atomic theory correctly depicts this law.
Looking Closer: Atomic Theory
Dalton’s ideas are called the modern atomic theory because the concept of atoms is very old. The Greek philosophers Leucippus and Democritus originally introduced atomic concepts in the fifth century BC. (The word atom comes from the Greek word atomos, which means “indivisible” or “uncuttable.”) Dalton had something that the ancient Greek philosophers didn’t have, however; he had experimental evidence, such as the formulas of simple chemicals and the behavior of gases. In the 150 years or so before Dalton, natural philosophy had been maturing into modern science, and the scientific method was being used to study nature. When Dalton announced a modern atomic theory, he was proposing a fundamental theory to describe many previous observations of the natural world; he was not just participating in a philosophical discussion.
Concept Review Exercises
-
What is the modern atomic theory?
-
What are atoms?
Answers
-
The modern atomic theory states that all matter is composed of atoms.
-
Atoms are the smallest parts of an element that maintain the identity of that element.
Key Takeaways
- Atoms are the ultimate building blocks of all matter.
- The modern atomic theory establishes the concepts of atoms and how they compose matter.
Example Problems
1. Basic concept check: When 32.0 grams (g) of methane are burned in 128.0 g of oxygen, 88.0 g of carbon dioxide and 72.0 g of water are produced. Which law is this an example of? (a) Law of definite proportions (b) Law of conservation of mass or (c) Law of multiple proportions.
The answer is (b) Law of conservation of mass. The number of grams of reactants (32.0 g of methane and 128.0 g of oxygen = 160.0 g total) is equal to the number of grams of product (88.0 g of carbon dioxide and 72.0 g of water = 160.0 g total).
2. Law of Conservation of Mass: 8.00 grams (g) of methane are burned in 32.00 g of oxygen. The reaction produces 22.00 g of carbon dioxide and an unmeasured mass of water. What mass of water is produced?
The answer is 18.00 g of water. Because the only products are water and carbon dioxide, their total mass must equal the total mass of the reactants, methane and oxygen. 8.00 g of methane + 32.00 g of oxygen = 40.00 total g of reactants. Because the total mass of the reactants equals the total mass of the products, the total mass of the products is also 40.00 g. Thus, 40.00 total g of products = 22.00 g carbon dioxide + unknown mass water. 40.00 total g of products - 22.00 g carbon dioxide = 18.00 g water.
3. Law of Definite Proportions: Two experiments using sodium and chlorine are performed. In the first experiment, 4.36 grams (g) sodium are reacted with 32.24 g of chlorine, using up all the sodium. 11.08 g of sodium chloride was produced in the first experiment. In the second experiment, 4.20 g of chlorine reacted with 20.00 g of sodium, using up all the chlorine. 6.92 g of of sodium chloride was produced in the second experiment. Show that these results are consistent with the law of constant composition.
To solve, determine the percent of sodium in each sample of sodium chloride. There is 4.36 g sodium for every 11.08 g of sodium chloride in the first experiment. The amount of sodium in the sodium chloride for the second experiment must be found. This is found by subtracted the known amount of reacted chlorine (4.20 g) from the amount of sodium chloride (6.92 g). 6.92 g sodium chloride - 4.20 g chlorine = 2.72 g sodium.
Thus, the percent of sodium in each sample is represented below:
% Na = (4.36 g Na)/(11.08 g NaCl) x 100% = 39.4% Na % Na = (2.72 g Na)/(6.92 g NaCl) x 100% = 39.3%
The slight difference in compositions is due to significant figures: each percent has an uncertainty of .01% in either direction. The two samples of sodium chloride have the same composition.
4. Law of Conservation of Mass: 36.0 grams (g) of wood are burned in oxygen. The products of this reaction weigh 74.4 g. (a) What mass of oxygen is needed in this reaction? (b) What mass of oxygen is needed to burn 8.00 lb of wood? 1 lb = 453.59237 g.
- The answer is 38.4 g of oxygen. The total mass of the products is 74.4 g. Thus, the total mass of the reactants must equal 74.4 g as well. Thus, 74.4 g products - 36.0 g wood reactant = 38.4 g oxygen reactant.
- The answer is 8.53 lb of oxygen. From, (a) that it takes 38.4 g of oxygen to burn 18.0 g of wood. First, convert both of these values to pounds (alternatively, the 8.00 lb can be converted to grams).
36.0 g wood x (1lb)/(453.59237 g) = .0793664144 lb wood
38.4 g oxygen x (1 lb)/(453.59237 g) = .0846575087 lb oxygen
Now two ratios equal to each other can be set up to determine the unknown mass of oxygen.
(0.0793664144 lb wood)/(.0846575087 lb oxygen) = (8.00 lb wood)/(unknown mass oxygen)
Solving reveals that it requires 8.53 lb of oxygen to burn 8.00 lb of wood.
5. Law of Definite Proportions: A sample of methane contains only carbon and hydrogen, with 3.00 grams (g) of carbon for every 1.00 g of hydrogen. How much hydrogen should be present in a different, 50.0 g same of methane?
The answer is 12.5 g of hydrogen. If there are 3.00 g of carbon present for every 1.00 g of hydrogen, we can assume the smallest whole number combination of these elements in that ratio to be 4.00 g of methane:
50.0 g methane x (1.00 g hydrogen)/(4.00 g methane) = 12.5 g of hydrogen.
Outside links
- Description of Atomic Theory - http://en.wikipedia.org/wiki/Atomic_theory
- Description of Atomic Theory - http://www.visionlearning.com/librar...wer.php?mid=50
- Cathode Ray Demonstration - http://www.youtube.com/watch?v=XU8nMKkzbT8
- Theoretical Demonstration of Conservation of Mass - http://www.youtube.com/watch?v=dExpJAECSL8
- Actual Demonstration of Conservation of Mass - http://www.youtube.com/watch?v=J5hM1...eature=related
- The alpha scattering experiment-http://www.youtube.com/watch?v=5pZj0u_XMbc
References
- Petrucci, Ralph, William Harwood, Geoffrey Herring, and Jeffry Madura. General Chemistry. 9th ed. Upper Saddle River, New Jersey: Pearson Prentince Hall, 2007
- Moore, John. Chemistry for Dummies. John Wiley & Sons Inc, 2002.
- Asimov, Isaac. A Short History of Chemistry. , CT.: Greenwood Press, 1965.
- Patterson, Elizabeth C. John Dalton and the Atomic Theory. Garden City, NY: Doubleday, 1970
- Myers, Richard. The Basics of Chemistry. Greenwood, 2003
- Demtröder, Wolfgang. Atoms, Molecules and Photons: An Introduction to Atomic- Molecular- and Quantum Physics. 1st ed. Springer. 2002
Exercises
-
Which of the following elements exist as diatomic molecules?
- helium
- hydrogen
- iodine
- gold
-
Which of the following elements exist as diatomic molecules?
- chlorine
- potassium
- silver
- oxygen
-
Why is it proper to represent the elemental form of helium as He but improper to represent the elemental form of hydrogen as H?
-
Why is it proper to represent the elemental form of chlorine as Cl2 but improper to represent the elemental form of calcium as Ca2?
Answers
-
- no
- yes
- yes
- no
-
Hydrogen exists as a diatomic molecule in its elemental form; helium does not exist as a diatomic molecule.

