Units, Measures and Dimensions
- Page ID
- 2167
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)CHEMTUTOR
Measurement is the most useful form of description in science. Often the most useful measurements are those that have a number and a unit, such as ‘12.7 inches.' Here '12.7' is the number and 'inches' is the unit. This unit of inches in the example is one of the common units in the dimension of length. A number, then, is an expression in numerals. A unit is a recognized way to divide the essence of a dimension for measurement, and a dimension is a measurable physical idea. Here is a bit of advice you can overlook only at your peril: To become fluent in the subject you should memorize the basic background of information. The following units, dimensions, and measures are so basic to the study of Chemistry that you could always help yourself by memorizing these. The real test of whether you know this well enough is to recognize the dimensions of any measurement and know its symbol and magnitude from the unit alone.
DIMENSIONS, UNITS, AND SYMBOLS
Notice the symbols of the dimensions as they would be used in formulas. The basic metric symbol or the symbol of the most used metric unit is listed after the metric units.
| DIMENSION | SYMBOL | METRIC UNITS | SYMBOL | “ENGLISH” UNITS |
| LENGTH | S, l, d, r | meter (+m.p.) | m | Ft, in,Yd, mi, etc. |
| AREA | A | sq.meter, etc,hectare | m2 | sq.Ft, etc., acre |
| VOLUME | V | cu.meter, etc., liter | m3, L | cu.Ft,cu.in,etc.,gal,Floz. |
| TIME | t | sec (+m.p.) sec,min,hr,day,yr,etc.(both metric & English) | ||
| MASS | m | Kilogram (+ m.p.), AMU | kg | (slug, rarely used) |
| FORCE (weight) | F, Fw | Newton (+ m.p.) | N | Pound (#), Oz, etc. |
| VELOCITY | v | meter/sec,KPH,etc | m/sec | Ft/sec, MPH, etc. |
| ACCELERATION | a | meter/sec.sq., etc. | m/sec2. | Ft/sec sq., etc. |
| PRESSURE | P | N/sq.m, atm.,Pa | atm,Pa* | #/sq.in (PSI), inHg, etc. |
| DENSITY | D | g/cc, Kg/liter, etc. | g/cc | #/cu.Ft, #/gal, etc. |
| TEMPERATURE | T | Celsius or Kelvin | °C | Fahrenheit or Rankine |
| ENERGY | E | Joule (+ m.p.) | J | foot-pound |
| HEAT | Q | calorie (+ m.p.) | cal | BTU (British Thermal Unit) |
| CONCENTRATION | C** | gram/L, mol/L, Molar | M | (#/gal or #/cu.ft, rare) |
Abbreviations: Ft = foot, in = inch, AMU = atomic mass unit, KPH = kilometers per hour, MPH = miles per hour,
gal = gallon, PSI = pounds per square inch, cc = cubic centimeter, inHg = inches of mercury, Pa = Pascal
m.p. = metric prefixes, cu. = cubic, sq. = square, atm = atmosphere.
*The unit Pa, for Pascal, is a unit of pressure that is the standard unit for the SI system, the MKS system in the metric measurements. The unit of Pascal, however, is rarely used in chemistry. Instead, the unit "atm," for "atmosphere," is still most used in chemistry.
**The symbol "B" is now the official symbol for concentration in the SI, but there are still chemistry texts using the "C" as is shown here."
The table above lists almost all the dimensions you will need in this course, the symbol for each dimension as it will be used in common formulas, and the units of each dimension. Notice Chemtutor has two systems of measurement displayed that you should know. There are really two commonly used metric subsystems. Most chemistry texts will use the MKS system (meter, kilogram, second) rather than the less-used CGS (centimeter, gram, second) system. A system is defined by its basic measure of distance, mass, and time.We will use the MKS system, also called the S.I., or International System. The symbol for only the basic unit of each dimension in the metric system is on the list.
METRIC SYSTEM vs. "ENGLISH SYSTEM"
The metric system typically uses only one root word for any basic dimension such as for length, the meter. All the metric units of length use the root word 'meter' with the metric prefixes in the next table. Our common system in the United States is not really a system, but is a thrown-together mess of measurements with no overriding order. Chemtutor, as does most of the United States, calls this group of measurements the “English system.” While calling it that is a considerable slander on the English people, the United States and Liberia are the only nations on earth to still cling to it. Chemtutor thinks that the English system makes a fine learning tool, along with being wonderfully poetic. You will want to know how to relate the English System to the metric system. Particularly notice the large number of units of length in the English system. This is only a small number of the common ones. We regularly use fathoms to measure depth in water and furlongs to measure distance in horse racing. There are many little-used English length units such as the barleycorn (one third of an inch) that may be picturesque, but are not used today. Notice that we define the barleycorn as a third of an inch. The way to relate one English unit to another is by definition. Length is the most common measurement. As a result, it has not only the largest number of words to describe it, but it also has the largest number of symbols to represent it in formulas. The English language also uses distance, long, width, height, radius, displacement, offset, and other words for length, sometimes in specialized applications.
LENGTH
A meter is a little longer than a yard, so a meterstick that has inches on the back of it will has just a bit over thirty-nine inches on the English side. Typically, on the English side, the inches are broken into halves, fourths, eighths, and perhaps sixteenths. On the metric side one meter breaks down into ten decimeters, one hundred centimeters, and a thousand millimeters.
AREA
An area is a length multiplied by a length. (A= l l as in the formula list.) An area is an amount of surface. Almost all area units are length units squared, such as: square meter (m2), square centimeter (cm2), square inch (in2), etc. The acre and hectare, units of land measurement, are the only units commonly used that are not in the ‘distance squared’ area unit format. An acre is defined as 43,560 square feet, so in using the unit 'acre' in dimensional analysis, the definition can be used to relate the acre to other units. Notice the squaring of a unit of length. A meter multiplied by a meter is a square meter. A foot by a foot is a square foot, etc.
VOLUME
Volume is length multiplied by length multiplied by length. You may have heard that volume is length times height times width, but it means the same thing. ( V= l l l ) You may think of a volume as the space inside a rectangular (block-shaped) fish tank. Volume is the measure of an amount of space in three dimensions. Because volume is such a common type of measurement, it is unique in that it has two types of commonly used root word in both metric and English systems. The metric roots are liter and cubic meter. The English system also uses cubic length and an extensive array of units that are not in the cubed length format. Again, analagously to area measurements, a cubic meter is a meter multiplied by a meter multiplied by a meter, and a cubic foot is a foot by a foot by a foot.
TIME
Time is also a bit odd in its units. In both systems the units of less than a second are in the metric style with prefixes before the second. Time units of more than a year are in a type of metric configuration because they are in multiples of ten. (Decades, centuries, millennia, etc.) The dimension of time is messy for good reason. The more commonly used time units from day to year are all dependent upon the movement of the earth. The unit of 'month,' particularly if it is directly related to the moon, is useless as an accurate unit because it does not come out even in anything. Having sixty seconds in an hour and twenty-four hours in a day come about from the ease of producing mechanical clocks. (Is it time to switch to metric time? How would you like, say, ten hours in a day, one hundred minutes in an hour, and one hundred seconds in a minute. It would come out to almost the same length of second.)
MASS
Mass is an amount of matter. Mass has inertia, which is the tendency of matter to stay where it is if it is not moving, or to keep moving at the same rate and direction if it is already moving. You could measure mass by an inertial massometer. Visualize a metal strip held tightly on one end and “twanged," or given a push to make it vibrate on the other end. It has a natural pitch to vibrate. If you were to put a mass on the end of that strip, you would change the pitch of the vibration. The change of pitch would make it possible to calculate the mass of the added object. This measurement of mass is completely independent of gravity, the way we often weigh a mass by comparing the push or force of the mass on a surface. Mass is a more accurate way of thinking of amount of matter compared to weight. The metric system is mass-based whereas the English system thinks in weight. Consider that an astronaut in near earth orbit has no weight because the gravitational attraction cancels inertia, but the mass of the astronaut remains the same. The metric root word of mass is the gram. Notice the difference between the ‘root word,’ gram, which is the basis for adding metric prefixes, and the system base of kilogram, the mass unit of the S.I. metric system.
FORCE
A force is a push or a pull. Those simple words are the best definition of a force under our limited experience. A force can not be seen or heard directly, so it is a bit of a difficult concept beyond the simple definition. Having basic metric units like 'kilogram-meter per second squared' make the idea of force hard to think about using that tool also.
WEIGHT
Weight is a downward force due to the mass of an object and the acceleration of gravity. The English system can conveniently use the idea of weight to measure amount of material because there is very little difference in the acceleration of gravity over the surface of the earth. There are certainly other forces besides gravity. Magnetism produces a force. Electric charge produces a force.
VELOCITY
Velocity is a complex dimension. The unit of velocity is a combination of more than one type of basic dimension. A velocity is a distance per time. The word 'per' here means 'divided by,' and distance divided by time is not only the definition of velocity, but it is the easy way to remember the velocity formula, v = d/t. Velocity also has the name of rate. You might know the same formula as, ‘rate times time equals distance.’ Here’s where we could start complicating the math by using calculus, but we won’t. If you are taking a course that requires calculus, the math is only slightly different, but the basic ideas behind it are the same.
ACCELERATION
An acceleration is just another step down the same road as velocity, that is, acceleration is a distance per time per time, or, another way to see it, distance per time squared. An acceleration is a time rate of change of velocity. If something changes its velocity, it has an acceleration. An acceleration causes an increase or decrease in speed or a change in direction. Newton and Einstein identified gravity as an acceleration. Gravity has a fairly consistent amount of acceleration on the surface of the earth, that is 32 ft./sec2 or 9.8 m/sec2. As you can see, the acceleration of gravity, ‘g,’ can substitute for the ‘a’ of acceleration in the formulas below when the acceleration is due to gravity.
PRESSURE
A pressure is a force per area. You can almost see the pressure of the wind on a sail. The pressure of the wind is the same, so the larger the area of the sail, the greater the force of the wind on the ship. Pressure unit definitions that we need for this course revolve around the unit ‘atmosphere’ because historically the pressure was first measured for weather.
DENSITY
Density is mass per volume, weight per volume, or specific gravity, which is the density of a material per the density of water. Metric system densities are usually in the units of mass per volume, such as kg/L (kilogram per liter) or g/cm3 (gram per cubic centimeter). English densities are usually in weight per volume, such as #/gal. (pounds per gallon) or #/ft3 (pound per cubic foot). Specific gravity has no units (!) because it is a comparative measurement. Specific gravity is the density of a material compared to the density of water. Expressing density as specific gravity shows neither system.
We can have fun in a density demonstration by passing a large-grapefruit-sized ball of lead around the class. That size of lead ball weighs about 35 pounds. People do not expect something that compact to weigh so much. One way to think of density is, ‘How much mass is packed into a volume.
TEMPERATURE
Temperature is a bit more subtle dimension. What we really measure is the average velocity of the atoms or molecules in the material. One way to measure it is by the expansion of a liquid in a very small tube. This is the shape of a liquid (usually mercury or alcohol) in a thermometer. The Fahrenheit scale is still not a bad one for use with weather. Scientists are more likely to use the Celsius or Centigrade scale. Gas law calculations require the Kelvin scale because it is an absolute scale. The other absolute scale, Rankine (pronounced “rank-in”), is useful for teaching purposes, but is not in common use.
ENERGY
Energy is the ability to do work. A Joule, the metric unit of energy is a kilogram- meter- square- per- second- square. Both of those ideas can be difficult to wrap your mind around. The easier way to think of energy is perhaps by its various types. You should have an intuitive feeling that a fifty pound rock held above your head has more energy of position in a gravitational field than the same fifty pound rock by your feet. A rubber band pulled back has more spring energy than a lax one. A speeding train has more energy of movement than a still one. We usually value petroleum not for its beauty, but for its chemical energy content. Energy is transferable from one type to another, but is not lost or gained in changes.
HEAT
Heat is a form of energy. It is the energy of the motion of molecules. Even though heat and energy are fundamentally the same dimension, we measure and calculate them differently. We define a calorie (note the lower-case 'c') as the amount of heat that increases the temperature of a gram of liquid water one degree C. The BTU, the English unit of heat, is the amount of heat that increases the temperature of a pound of liquid water one degree F. A food Calorie (note upper case 'C' ) is one thousand heat calories of usable food energy. That is, the food Calorie reflects the type of living thing eating AND USING the energy. So the food Calorie depends on the type of (animal) eating it. A cow or a termite could get much more food value from a head of lettuce than a human being can, so what is a Calorie for us would be different for them.
CONCENTRATION
Concentration is amount of material in a volume. In this course, we will stay mostly with measuring the amount of solute in a solution. There is more on this in the chapter on solutions, and we really need to explain the idea of mol or mole before a thorough explanation of concentration can mean much. <basefont size="4"/> Notice the formulas in the table below. Some of the simple ones we use in this course only for practice with problem-solving techniques and for defining the units and dimensions. There are a few items in the formulas that have not been mentioned yet, such as c, the specific heat; n, the number of mols; and R, the universal gas constant. These we will consider in context as we use them.
FORMULAS
| A = l l | V = l l l | V = A l | v t = d | F = m a ( Fw = m g) |
| a = v/t | a = d/t2 | P = F/A | C V = n | D = m/V (D =Fw/V) |
| P V = n R T | Q = m c | Circle Area, Ac = | ||
A formula is a relationship among dimensions. The symbols for the dimensions in the formula list are in the dimension list. Note the capitalization or lack of it in the symbols, for instance, V = volume and v = velocity; C = concentration and c = specific heat, etc. Also, there are some letters written after and slightly under a symbol called a subscript. Subscripts indicate a special case of the symbol, as you see above with the area of a circle being represented by the A for area and a subscript c for circle.
DEFINITIONS TO CHANGE UNITS
There are three types of definitions you should know for changing units:
- English system definitions
- metric system definitions and
- changeover definitions between the two systems.
There are a small number of English system definitions listed below in Table C that you should know by rote. Notice that we take the same approach here with one of the larger unit being stated first and then some number greater than one of the smaller unit. All of these English definitions are exact definitions except for the cubic feet-to-gallons relationship. Take a look at any edition of the Chemical Rubber Company (CRC) Handbook of Physics and Chemistry and you will see the incredible number of non-metric units.
ENGLISH SYSTEM DEFINITIONS YOU SHOULD KNOW BY ROTE
| 1 ft. = 12 in. | 1 mi. = 5280 ft. | 1 cup = 8 Floz. | 1 pint = 2 cups | 1 qt. = 2 pints |
| 1 gal. = 4 qts. | 1 # = 16 Oz. | 1 ton = 2000 # | 1 acre = 43560 ft2 | *1 ft3 = 7.48 gal. |
| 1 gal. = 231 in3 | *not an exact def. |
METRIC PREFIXES AS FACTORS OF TEN
| FACTOR | PREFIX | SYMBOL |
| +18 | exa | E |
| +15 | peta | P |
| +12 | tera | T |
| +9 | giga | G |
| +6 | mega | M |
| +3 | kilo | k |
| +2 | hecto | h |
| +1 | deka | da |
| 0 | *ROOT WORD ONLY* | |
| -1 | deci | d |
| -2 | centi | c |
| -3 | milli | m |
| -6 | micro | µ |
| -9 | nano | n |
| -12 | pico | p |
| -15 | femto | f |
| -18 | atto | a |
The above table includes only the commonly used metric prefixes. There have been some metric prefixes suggested for some of the exponents of ten not listed here, but they are not in common use, or are in use by only a small number of people for limited use. The prefix "myria-" (my or ma) as E4 is a good example. The word "myriad" means ten-thousand, so the prefix is well documented in language. (Thanks to Van Isaac Anderson for the thought.)
A FEW ODD METRIC DEFINITIONS
| 1 metric tonne = E3 kg | 1 mL. = 1 cc = 1 cm3 |
| 1 Ångstrom = E-10 m | 1 cubic meter = 1000 L |
THE METRIC STAIRCASE
| | peta +15 | The metric staircase below is a graphic way of showing how | |||||||||||||||||||||||||||||||
| |__ | metric prefixes interact. It is the same thing as the chart | |||||||||||||||||||||||||||||||
| |__ | above, but in a more visual representation. Each step is | |||||||||||||||||||||||||||||||
| | tera +12 | a multiple of ten of the lower step. For instance, 'centi' | |||||||||||||||||||||||||||||||
| |__ | is on the next step above 'milli,' so a centimeter is | |||||||||||||||||||||||||||||||
| |__ | ten times larger than a millimeter. Centigram is | |||||||||||||||||||||||||||||||
| | giga +9 | ten times larger than milligram. There are no | |||||||||||||||||||||||||||||||
| |__ | common metric prefixes for some powers | |||||||||||||||||||||||||||||||
| |__ | of ten such as +4,+5,-7, etc. | |||||||||||||||||||||||||||||||
| | mega +6 | ||||||||||||||||||||||||||||||||
| |__ | ||||||||||||||||||||||||||||||||
| |__ | ||||||||||||||||||||||||||||||||
| | kilo +3 | ||||||||||||||||||||||||||||||||
| | hecto +2 | ||||||||||||||||||||||||||||||||
| | deka +1 | ||||||||||||||||||||||||||||||||
| | ROOT WORD | ||||||||||||||||||||||||||||||||
| | deci -1 | ||||||||||||||||||||||||||||||||
| | centi -2 | ||||||||||||||||||||||||||||||||
| | milli -3 | ||||||||||||||||||||||||||||||||
| |__ | ||||||||||||||||||||||||||||||||
| METRIC SYSTEM DEFINITIONS | |__ | |||||||||||||||||||||||||||||||
| | micro -6 | ||||||||||||||||||||||||||||||||
| Metric system definitions are relationships | |__ | |||||||||||||||||||||||||||||||
| between units with the same rootword that, | |__ | |||||||||||||||||||||||||||||||
| is, only the prefix changes. The Metric Stair- | | nano -9 | |||||||||||||||||||||||||||||||
| case is just a way to visualize the relationships | |__ | |||||||||||||||||||||||||||||||
| among the metric prefixes. We make a metric | |__ | |||||||||||||||||||||||||||||||
| system definition in the following way, using the | | pico -12 | |||||||||||||||||||||||||||||||
| units kilometer and millimeter as an example: | |__ | |||||||||||||||||||||||||||||||
| |__ | ||||||||||||||||||||||||||||||||
| 1.Pick the largest metric prefix. Begin the metric definition with | |femto-15 | |||||||||||||||||||||||||||||||
| one of the larger units, e.g. 1 km = (some number of) millimeters. | | _ | |||||||||||||||||||||||||||||||
2. Count the number of 'steps' down the metric staircase between the two metric prefixes. For instance, kilo- to milli- is six steps.
3. The number of the smaller unit is ten to the power of the number of steps between the metric prefixes. In our example
1 km = 106 mm. Another way to think of it is that the number of zeros of the smaller unit is the number of steps, so
1 km = 1,000,000 mm.
The reason for stating the metric system definitions this way is to make calculations easier and make the sense of the definition more obvious. It is easier to use 1 km = E6 mm than 1 mm = 1/1,000,000 km in math, even though they are both correct.
Here is more information on the metric units, their origins and uses. This chart emphasizes the point of view of computer use.
There are some times you will need to convert between systems. The following few conversion definitions are all you should need to memorize to convert almost anything. Notice we show a “bridge” between the systems in length, volume, and mass to weight
COMMONLY USED CONVERSIONS FROM METRIC TO ENGLISH
| 1 kg = 2.2 # (at “g”) or 1 # (at 'g') = 453 grams (Use either of these two.) | |
These three conversions are all you will need in this course. The DA (dimensional analysis) system will use these to convert more complex units. See the DA problems at the end of Numbers and Math for more understanding as to how these conversion factors work. As you need them for whatever you might do on a regular basis, you might need to find conversions that are more useful to you. A cook might want a conversion factor between cups and liters. A doctor or pharmacist might want a conversion factor between grains and grams. The conversion between inches and centimeters is an exact one by definition, but the others are not. The conversion from metric mass to English weight must be done assuming the acceleration of gravity is one g.
Particularly in the section on gases you will need the following pressure units:
1 atm = 760 mmHg = 33.9 ftH2O = 14.7 PSI = 29.96 inHg ≈ 30 inHg
Abbreviations: atm = atmosphere, mmHg = millimeters of mercury, PSI = pounds per square inch, ftH2O = feet of water, inHg = inches of mercury. The unit ‘feet of water’ is not common, but included because it can be useful. For every hundred feet below the surface of water the pressure increases about three atmospheres. The running equation above (It just keeps going!) shows the common pressure units. You can use it to change between any two of the units, for example:
760 mmHg = 14.7 PSI.
The official SI unit of pressure, the Pascal, Pa, is not often used in chemistry because it is such a small unit. One atmosphere is about equal to 100,000 Pascals, or you could say that one atmosphere is approximately equal to 100 kPa.
More exactly, 1 atm = 1.01325 E5 Pa = 101.325 kPa
ISLAND SYSTEMS
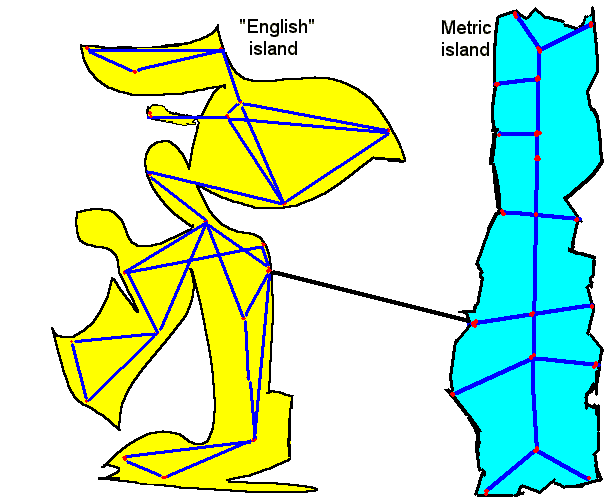
Here is one way to think of the metric and "English" systems. The metric system is the metric island with an orderly set of towns and an orderly and simple and fast road system. The "English" island has every town connected as well as they can (by definitions) to other neighboring towns. The "English" system of transportation is not too efficient.
There only has to be one good solid bridge (changeover definition) between the two islands. You can get anywhere from one system to the other by first coming to the bridge town, crossing, and then taking the new system to wherever you want to go.
Metric prefix humor (?) exa-ray exa-rated peta-cat tera-dactyl giga-low tera-bull pico-nose deci-mate tera-piece-of-paper peta-greed tara-rism pico-peach deca-cards atto-mobile micro-phone nano-pudding milli-mouse milli-cent pico-card peta-gogue peta-ful pico-nick ba-nano pico-low centi-mental exa-lint atto-miser milli-tent pico-boo atto-whack tera-pin kilo-bug deca-ration centi-fold tera-torialism
THERE'S MORE
1 million microphones = 1 megaphone
2000 mockingbirds = two kilomockingbirds
10 cards = 1 decacards
1 millionth of a fish = 1 microfiche
453.6 graham crackers = 1 pound cake
1 trillion pins = 1 terrapin
10 rations = 1 decoration
100 rations = 1 C-ration
10 millipedes = 1 centipede
3 1/3 tridents = 1 decadent
AND EVEN MORE
2 monograms = 1 diagram
8 nickels = 2 paradigms
2 wharves = 1 paradox
Contributors
- David Wilner (info@chemtutor.com)
- Ellen Averill
| Copyright © 1997-2009 Chemtutor, LLC. All rights reserved. |
| Publication of any part is prohibited without prior written consent, except for instructor use publishing for instructor's own classroom students. All hard copy materials distributed under this exception must have on every page distributed reference to http://www.chemtutor.com as source. Under the same exception granted to classroom teachers, full recognition of Chemtutor must be given when all or any part is included in any other electronic representation, such as a web site, whether by direct inclusion or by hyperlink. |

