Chapter 4 Solutions
- Page ID
- 1119
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In-chapter exercises
E4.1:
a) You would expect to see fragments of m/z = 15, 29, 43, 57, and 72.
b) You would expect to see fragments of m/z = 29, 43 (cations); 57, 71 (acylium ions), and 102 (molecular ion).
c) All of the fragmentation events shown in the example would lead to fragments with m/z = 84.
E4.2: Chlorine has two main isotopes of mass 35 (abundance ~76%) and 37 (abundance ~24%). Therefore, fragments containing Cl would be seen in pairs with relative heights of about 3:1.
E4.3: The mass spectrum fits that of propanal. The most abundant fragment (the base peak) is the acylium ion containing the aldehyde hydrogen.
E4.4:
Using λν = c, we first rearrange to ν= c/λ to solve for frequency.
For light with a wavelength of 400 nm, the frequency is 7.50 x 1014 Hz:

In the same way, we calculate that light with a wavelength of 700 nm has a frequency of 4.29 x 1014 Hz.
To calculate corresponding energies:
Using hc/λ, we find for light at 400 nm:
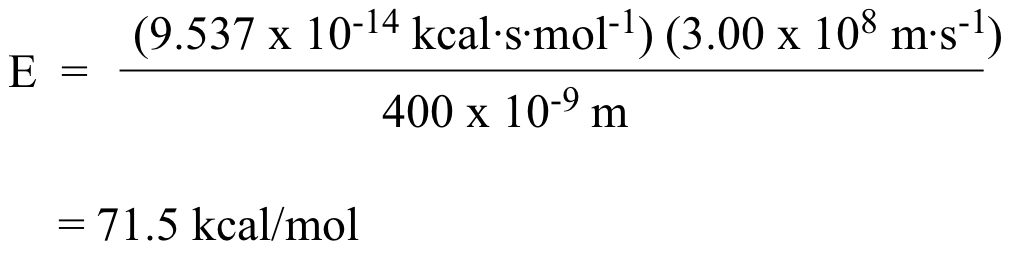
Using the same equation, we find that light at 700 nm corresponds to 40.9 kcal/mol.
E4.5:
A wavenumber of 3000 cm-1 means that 3000 waves fit in one cm (0.01m):
![]()
We want to find the length of 1 wave, so we divide numerator and denominator by 3000:
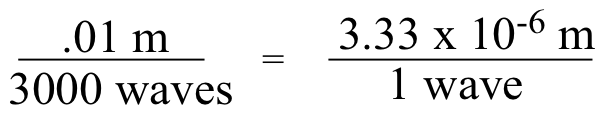
So 3000 cm-1 is equivalent to a wavelength of 3.33 mm.
E4.6: We can distinguish the alkenes from the alkenes by their respective C-C stretching bands. To distinguish between the two alkenes, we recognize that1,3-octadiene will have characteristic vinylic C-H stretching bands, whereas 1,2-dimethylcyclohexene will not. In a similar argument, 1-octyne will show a terminal alkyne C-H stretching band, while 3-octyne will not.
E4.7: Using the online Spectral Database for Organic Compounds, look up IR spectra for the following compounds, and identify absorbance bands corresponding to those listed in the table above. List actual frequencies for each signal to the nearest cm-1 unit, using the information in tables provided on the site.
a) 1-methylcyclohexanol: O-H stretching centered at 3375 cm-1
b) 4-methylcyclohexene: alkene C-H stretching at 3025 cm-1; alkene C-C stretching at 1651 cm-1
c) 1-hexyne: terminal alkyne C-H stretching at 3311cm-1, alkyne C-C stretching at 2120 cm-1.
d) 2-hexyne: alkyne C-C stretching at 2054 cm-1 (this signal is very weak, because the molecule is near-symmetrical and thus the triple bond has only a very weak dipole moment)
e) 3-hexyne-2,5-diol: O-H stretching centered on 2983. No alkyne C-C stretching band because the molecule is symmetrical.
E4.8: As carbon-carbon bonds get shorter and stronger moving from single to double to triple order, the stretching frequency becomes higher, meaning shorter wavelengths (higher wavenumbers) . Imagine two balls connected by a short, tight spring compared to the same two balls connected to a longer, looser spring. If you compress and release both springs so that the balls bounce back and forth, the shorter spring will bounce more rapidly (higher frequency).
E4.9: Using the same method as in Exercise 4.4, we find that photons of light with wavelength of 470 nm have energy of 255 kJ/mol.
E4.10: Molecule A has a longer system of conjugated pi bonds, and thus will absorb at a longer wavelength. Notice that there is an sp3-hybridized carbon in molecule B which isolates two of the pi bonds from the other three.
E4.11:
We use the formula:
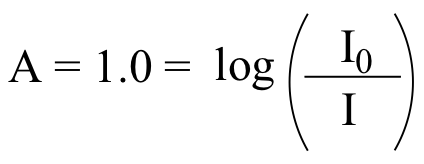
recall from your high school algebra that if y = log(x), then x = 10y , so:
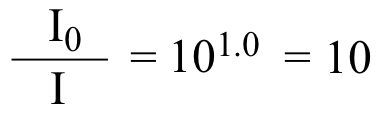
. . . so the intensity of light entering the sample (I0) is 10 times the intensity of the light (at a particular wavelength) that emerges from the sample and is detected (I). Because %T is simply the reciprocal of this ratio multiplied by 100, we find that A = 1.0 corresponds to 10% transmission.
E4.6: Using ε = A/c, we plug in our values for ε and A and find that c = 3.27 x 10-5M, or 32.7 mM.
End-of-chapter problems
P4.1:
Without doing any calculation, we can answer the first part of the calculation: electromagnetic waves at 3400 cm-1 are shorter than those at 1690 cm-1 (more waves fit into one centimeter) and thus correspond to a higher frequency.
3400 cm-1 = 2.94 mm = 1.02 x 1014 Hz
1690 cm-1 = 5.92 mm = 5.07 x 1013 Hz
P4.2:
1720 cm-1 corresponds to a wavelength of .01/1720 = 5.81 x 10-6 m, and an energy of 4.92 kcal/mol.
P4.3:
The triple bond in compound I is symmetric, and therefore is not IR-active, so there would be no absorbance in the carbon-carbon triple bond range (2100-2250 cm-1). In compound II the presence of the fluorines makes the triple bond asymmetric and IR-active, thus the alkyne peak will be observed. In compound III, we should see not only the carbon-carbon triple bond peak but also an absorbance at approximately 3300 cm-1 due to stretching of the terminal alkyne carbon-hydrogen bond.
P4.4:
All three spectra will have a strong carbonyl stretching peak, but the ester (compound C) carbonyl peak will be observed at a shorter wavelength compared to the ketone (compound B) and the carboxylic acid (compound A). In addition, Compound A will show a broad absorbance centered at approximately 3000 cm-1 due to carboxylic acid O-H stretching, whereas in the spectrum of compound B we should see the broad absorbance centered at approximately 3300 cm-1 from stretching of the alcohol O-H bond. Compound C will have no broad O-H stretching absorbance.
P4.5:
All three compounds contain alkene functional groups. However, in compound Y the alkene is symmetric and thus we would not expect to see an absorbance from C=C stretching in the 1620-1680 cm-1range. We would expect to see this peak in the spectra of compounds X and Z; in addition we would expect to see, in the compound X spectrum, a peak in the 3020 - 3080 cm-1 range due to stretching of the terminal alkene C-H bonds.
P4.6:
![]()
![]()
P4.7:
The change in A340 is DA = 0.220. Using the expression ε = A/c, we can calculate that this represents a change in the NADH concentration of 3.50 x 10-5 M. This is in a 1 mL solution, so 3.50 x 10-8 mol have been used up over the course of five minutes, or 7.00 x 10-9 mol (7.00 nmol) per minute on average.
P4.8:
Both starting compounds contain systems of conjugated pi bonds which absorb in the UV range. The condensation reaction brings these two conjugated systems together to create a single, longer conjugated pi system, which absorbs in the blue part of the visible spectrum.
P4.9:
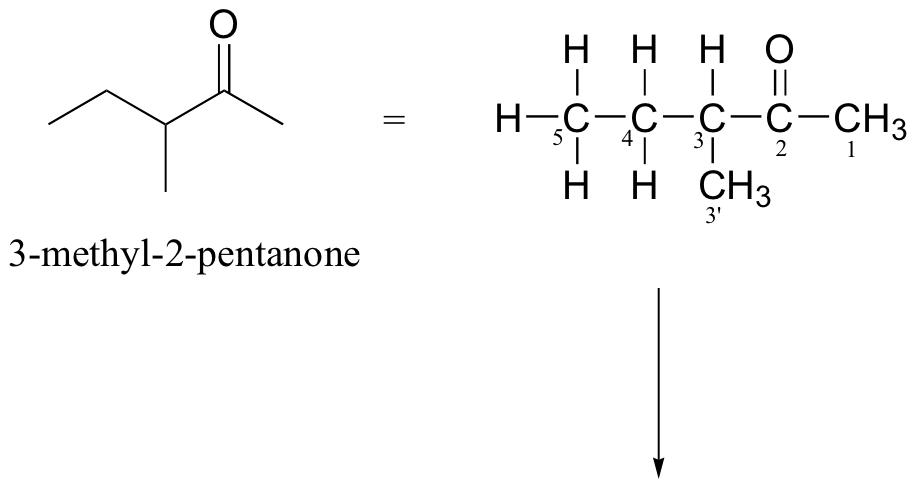

P4.10:
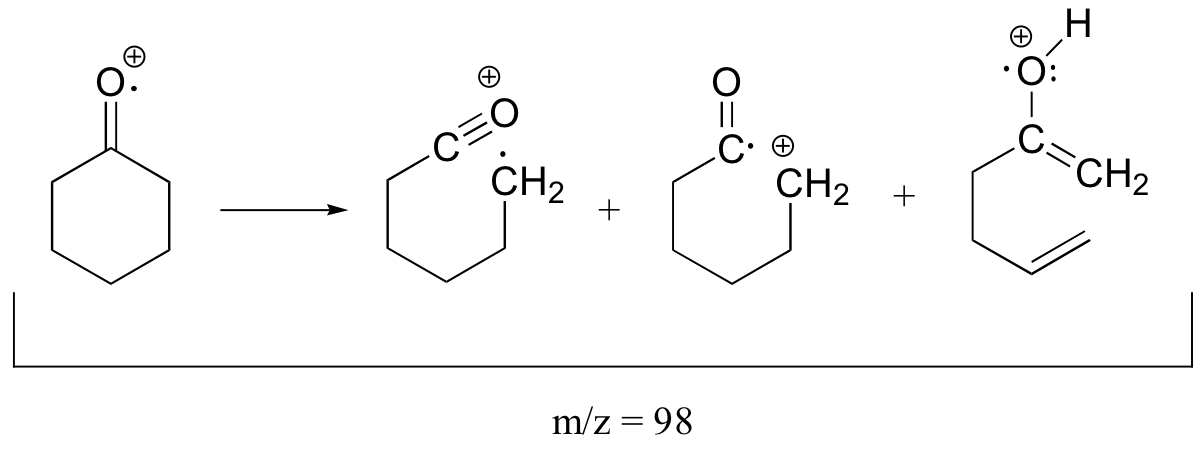
The molecular ion and the fragments from all three of the typical ketone fragmentation patterns would all have m/z = 98.
P4.11:
Both molecules contain alkene and ketone functional groups, however the degree of pi bond conjugation is different. Therefore, UV would be the more useful technique to distinguish the two.
P4.12:
Both molecules are straight-chain alkanes with a single ketone group, so their IR spectra are expected to be very similar and neither will absorb strongly in the UV range. However, the different positions of the ketone (at the C4 vs C5 position) will result in the formation of fragments of different masses in an MS experiment.


