11.3: Coulometric Methods
- Page ID
- 5603
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In a potentiometric method of analysis we determine an analyte’s concentration by measuring the potential of an electrochemical cell under static conditions. Dynamic techniques, in which current passes through the electrochemical cell, also are important electrochemical methods of analysis. In this section we consider coulometry. Voltammetry and amperometry are covered in section 11D.
Coulometry is based on an exhaustive electrolysis of the analyte. By exhaustive we mean that the analyte is completely oxidized or reduced at the working electrode or that it reacts completely with a reagent generated at the working electrode. There are two forms of coulometry: controlled-potential coulometry, in which we apply a constant potential to the electrochemical cell, and controlled-current coulometry, in which we pass a constant current through the electrochemical cell.
During an electrolysis, the total charge, \(Q\), in coulombs, passing through the electrochemical cell is proportional to the absolute amount of analyte by Faraday’s law
\[Q = nFN_\ce{A} \tag{11.25}\]
where n is the number of electrons per mole of analyte, F is Faraday’s constant (96487 C mol–1), and NA is the moles of analyte. A coulomb is equivalent to an A⋅sec; thus, when passing a constant current, i, the total charge is
\[Q=it_\ce{e} \tag{11.26}\]
where te is the electrolysis time. If the current varies with time, as it does in controlled-potential coulometry, then the total charge is
\[Q = \int_o^{t_\ce{e}} i(t)\;dt \tag{11.27}\]
In coulometry, we monitor current as a function of time and use either equation 11.26 or equation 11.27 to calculate Q. Knowing the total charge, we then use equation 11.25 to determine the moles of analyte. To obtain an accurate value for NA, all the current must be used to oxidize or reduce the analyte. In other words, coulometry requires 100% current efficiency—or an accurately measured current efficiency established using a standard—a factor that we must be consider when designing a coulometric method of analysis.
Note
Current efficiency is the percentage of current that actually leads to the analyte’s oxidation or reduction.
11.3.1 Controlled-Potential Coulometry
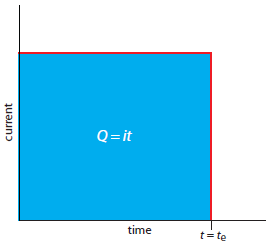
The easiest way to ensure 100% current efficiency is to hold the working electrode at a constant potential, chosen so that the analyte reacts completely without simultaneously oxidizing or reducing an interfering species. As electrolysis progresses the analyte’s concentration decreases, as does the current. The resulting current-versus-time profile for controlled-potential coulometry is shown in Figure 11.27. Integrating the area under the curve (equation 11.27) from t = 0 to t = te gives the total charge. In this section we consider the experimental parameters and instrumentation needed to develop a controlled-potential coulometric method of analysis.
Figure 11.27 Current versus time for a controlled-potential coulometric analysis. The measured current is shown by the red curve. The integrated area under the curve, shown in blue, is the total charge.
Selecting a Constant Potential
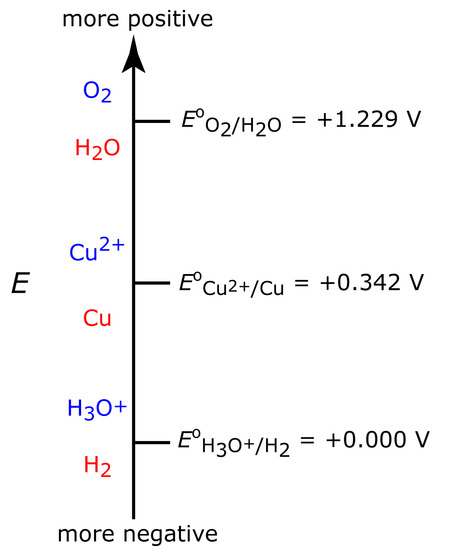
To see how an appropriate potential for the working electrode is selected, let’s develop a constant-potential coulometric method for Cu2+ based on its reduction to copper metal at a Pt working electrode.
\[\ce{Cu^2+}(aq) + 2e^- ⇋ \ce{Cu}(s)\tag{11.28}\]
Figure 11.28 shows a ladder diagram for an aqueous solution of Cu2+. From the ladder diagram we know that reaction 11.28 is favored when the working electrode’s potential is more negative than +0.342 V versus the standard hydrogen electrode. To ensure a 100% current efficiency, however, the potential must be sufficiently more positive than +0.000 V so that the reduction of H3O+ to H2 does not contribute significantly to the total current flowing through the electrochemical cell.
Figure 11.28 Ladder diagram for an aqueous solution of Cu2+ showing steps for the reductions of O2 to H2O, of Cu2+ to Cu, and of H3O+ to H2. For each step, the oxidized species is in blue and the reduced species is in red.
We can use the Nernst equation for reaction 11.28 to estimate the minimum potential for quantitatively reducing Cu2+.
\[E = E^\circ_\mathrm{Cu^{2+}/Cu} - \dfrac{0.05916}{2}\log\dfrac{1}{[\mathrm{Cu^{2+}}]}\tag{11.29}\]
Note
So why are we using the concentration of Cu2+ in equation 11.29 instead of its activity? In potentiometry we write the Nernst equation using activity because we use Ecell to determine the amount of analyte in the sample. Here we are using the Nernst equation to design the analysis. The amount of analyte is given by the total charge, not the applied potential.
If we define a quantitative electrolysis as one in which we reduce 99.99% of Cu2+ to Cu, then the concentration of Cu2+ at te is
\[[\ce{Cu^2+}]_{t_\ce{e}} = 0.0001×[\ce{Cu^2+}]_0\tag{11.30}\]
where [Cu2+]0 is the initial concentration of Cu2+ in the sample. Substituting equation 11.30 into equation 11.29 allows us to calculate the desired potential.
\[E = E^\circ_\mathrm{Cu^{2+}/Cu} − \dfrac{0.05916}{2}\log\dfrac{1}{0.0001×[\ce{Cu^2+}]_0}\]
If the initial concentration of Cu2+ is 1.00 × 10–4 M, for example, then the working electrode’s potential must be more negative than +0.105 V to quantitatively reduce Cu2+ to Cu. Note that at this potential H3O+ is not reduced to H2, maintaining 100% current efficiency.
Note
Many controlled-potential coulometric methods for Cu2+ use a potential that is negative relative to the standard hydrogen electrode—see, for example, Rechnitz, G. A. Controlled-Potential Analysis, Macmillan: New York, 1963, p.49.
Based on the ladder diagram in Figure 11.28 you might expect that applying a potential <0.000 V will partially reduce H3O+ to H2, resulting in a current efficiency that is less than 100%. The reason we can use such a negative potential is that the reaction rate for the reduction of H3O+ to H2 at is very slow at a Pt electrode. This results in a significant overpotential—the need to apply a more positive or a more negative potential than predicted by thermodynamics—that shifts Eo for the H3O+/H2 redox couple to a more negative value.
Minimizing Electrolysis Time
In controlled-potential coulometry, as shown in Figure 11.27, the current decreases over time. As a result, the rate of electrolysis—recall from Section 11A that current is a measure of rate—becomes slower and an exhaustive electrolysis of the analyte may require a long time. Because time is an important consideration when choosing and designing analytical methods, we need to consider the factors affecting the analysis time.
We can approximate the change in current as a function of time in Figure 11.27 by an exponential decay; thus, the current at time t is
\[i = i_0e^{-kt}\tag{11.31}\]
where i0 is the current at t = 0 and k is a rate constant that is directly proportional to the area of the working electrode and the rate of stirring, and that is inversely proportional to the volume of solution. (Problem11.16 asks you to explain why a larger surface area, a faster stirring rate, and a smaller volume leads to a shorter analysis time.) For an exhaustive electrolysis in which we oxidize or reduce 99.99% of the analyte, the current at the end of the analysis, te, is
\[i ≤ 0.0001 × i_0\tag{11.32}\]
Substituting equation 11.32 into equation 11.31 and solving for te gives the minimum time for an exhaustive electrolysis as
\[t_\ce{e}= -\dfrac{1}{k} × \ln(0.0001) = \dfrac{9.21}{k}\]
From this equation we see that a larger value for k reduces the analysis time. For this reason we usually carry out a controlled-potential coulometric analysis in a small volume electrochemical cell, using an electrode with a large surface area, and with a high stirring rate. A quantitative electrolysis typically requires approximately 30–60 min, although shorter or longer times are possible.
Instrumentation
A three-electrode potentiostat is used to set the potential in controlled-potential coulometry. The working electrodes is usually one of two types: a cylindrical Pt electrode manufactured from platinum-gauze (Figure 11.29), or a Hg pool electrode. The large overpotential for the reduction of H3O+ at Hg makes it the electrode of choice for an analyte requiring a negative potential. For example, a potential more negative than –1 V versus the SHE is feasible at a Hg electrode—but not at a Pt electrode—even in a very acidic solution. Because mercury is easily oxidized, it is less useful if we need to maintain a potential that is positive with respect to the SHE. Platinum is the working electrode of choice when we need to apply a positive potential.
Note
Figure 11.5 shows an example of a manual three-electrode potentiostat. Although a modern potentiostat uses very different circuitry, you can use Figure 11.5 and the accompanying discussion to understand how we can use the three electrodes to set the potential and monitor the current.
Figure 11.29 Example of a cylindrical Pt-gauze electrode for controlled-potential coulometry. The electrode shown here has a diameter of 13 mm and a height of 48 mm, and is fashioned using Pt wire with a diameter of approximately 0.15 mm. The electrode’s surface has 360 openings/cm2 and a total surface area of approximately 40 cm2.
The auxiliary electrode, which is often a Pt wire, is separated by a salt bridge from the analytical solution. This is necessary to prevent the electrolysis products generated at the auxiliary electrode from reacting with the analyte and interfering in the analysis. A saturated calomel or Ag/AgCl electrode serves as the reference electrode.
The other essential instrumental need for controlled-potential coulometry is a means for determining the total charge. One method is to monitor the current as a function of time and determine the area under the curve, as shown in Figure 11.27. Modern instruments use electronic integration to monitor charge as a function of time. The total charge at the end of the electrolysis is read directly from a digital readout.
Electrogravimetry
If the product of controlled-potential coulometry forms a deposit on the working electrode, then we can use the change in the electrode’s mass as the analytical signal. For example, in we apply a potential that reduces Cu2+ to Cu at a Pt working electrode, the difference in the electrode’s mass before and after electrolysis is a direct measurement of the amount of copper in the sample. We call an analytical technique that uses mass as a signal a gravimetric technique; thus, we call this electrogravimetry.
Note
For a review of other gravimetric techniques, see Chapter 8.
11.3.2 Controlled-Current Coulometry
A second approach to coulometry is to use a constant current in place of a constant potential, which produces the current-versus-time profile shown in Figure 11.30. Controlled-current coulometry has two advantages over controlled-potential coulometry. First, the analysis time is shorter because the current does not decrease over time. A typical analysis time for controlled-current coulometry is less than 10 min, compared to approximately 30–60 min for controlled-potential coulometry. Second, because the total charge is simply the product of current and time (equation 11.26), there is no need to integrate the current-time curve in Figure 11.30.
Figure 11.30 Current versus time for a controlled-current coulometric analysis. The measured current is shown by the red curve. The integrated area under the curve, shown in blue, is the total charge.
Using a constant current presents us with two important experimental problems. First, during electrolysis the analyte’s concentration—and, therefore, the current due to the its oxidation or reduction—continuously decreases (see Figure 11.27). To maintain a constant current we must allow the potential to change until another oxidation reaction or reduction reaction occurs at the working electrode. Unless we design the system carefully, this secondary reaction decreases the current efficiency to less than 100%. The second problem is that we need a method for determining when the analyte's electrolysis is complete. As shown in Figure 11.27, in a controlled-potential coulometric analysis we know that electrolysis is complete when the current reaches zero, or when it reaches a constant background or residual current. In a controlled-current coulometric analysis, however, current continues to flow even when the analyte’s electrolysis is complete. A suitable method for determining the reaction’s endpoint, te, is needed.
Maintaining Current Efficiency
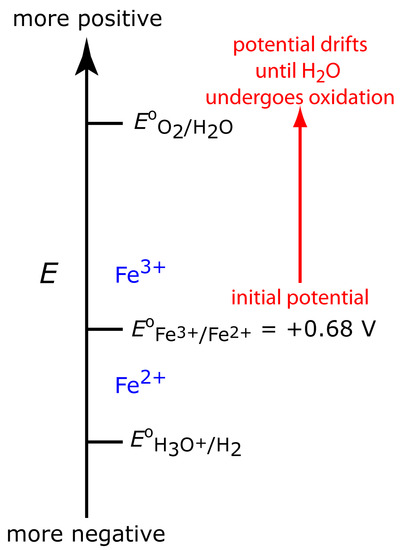
To illustrate why a change in the working electrode’s potential may result in a current efficiency <100%, let’s consider the coulometric analysis for Fe2+ based on its oxidation to Fe3+ at a Pt working electrode in 1 M H2SO4.
\[\ce{Fe^2+}(aq) ⇋ \ce{Fe^3+}(aq) + e^-\]
Figure 11.31 shows the ladder diagram for this system. At the beginning, the potential of the working electrode remains nearly constant at a level near its initial value. As the concentration of Fe2+ decreases, the working electrode’s potential shifts toward more positive values until the oxidation of H2O begins.
\[\ce{2H2O}(l)⇋\ce{O2}(g) + \ce{4H+}(aq) + 4e^-\]
Because a portion of the total current comes from the oxidation of H2O, the current efficiency for the analysis is less than 100% and we cannot use equation 11.25 to determine the amount of Fe2+ in the sample.
Figure 11.31 Ladder diagram for the constant-current coulometric analysis of Fe2+. The red arrow and text shows how the potential drifts to more positive values, decreasing the current efficiency.
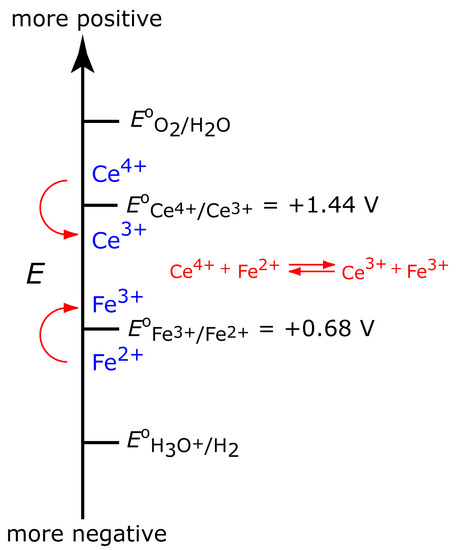
Although we cannot prevent the potential from drifting until another species undergoes oxidation, we can maintain a 100% current efficiency if the product of that oxidation reacts both rapidly and quantitatively with the remaining Fe2+. To accomplish this we can add an excess of Ce3+ to the analytical solution. As shown in Figure 11.32, when the potential of the working electrode shifts to a more positive potential Ce3+ eventually begins to oxidize.
\[\ce{Ce^3+}(aq) ⇋ \ce{Ce^4+}(aq) + e^- \tag{11.33}\]
The Ce4+ that forms at the working electrode rapidly mixes with the solution where it reacts with any available Fe2+.
\[\ce{Ce^4+}(aq) + \ce{Fe^2+}(aq) ⇋ \ce{Ce^3+}(aq) + \ce{Fe^3+}(aq)\tag{11.34}\]
Combining reaction 11.33 and reaction 11.34 shows that the net reaction is the oxidation of Fe2+ to Fe3+
\[\ce{Fe^2+}(aq) ⇋ \ce{Fe^3+}(aq) + e^-\]
maintaining a current efficiency of 100%. A species, such as Ce3+, which is used to maintain 100% current efficiency, is called a mediator.
Figure 11.32: Ladder diagram for the constant-current coulometric analysis of Fe2+ in the presence of a Ce3+ mediator. As the potential drifts to more positive values, we eventually reach a potential where Ce3+ undergoes oxidation. Because Ce4+, the product of the oxidation of Ce3+, reacts with Fe2+, we maintain current efficiency.
Endpoint Determination
Adding a mediator solves the problem of maintaining 100% current efficiency, but it does not solve the problem of determining when the analyte's electrolysis is complete. Using our same example, when the oxidation of Fe2+ is complete current continues to flow from the oxidation of Ce3+, and, eventually, the oxidation of H2O. What we need is a signal that tells us when there is no more Fe2+ in solution.
For our purposes, it is convenient to treat a controlled-current coulometric analysis as a reaction between the analyte, Fe2+, and the mediator, Ce3+, as shown by reaction 11.34. This reaction is identical to a redox titration; thus, we can use the end points for a redox titration—visual indicators and potentiometric or conductometric measurements—to signal the end of a controlled-current coulometric analysis. For example, ferroin provides a useful visual endpoint for the Ce3+ mediated coulometric analysis for Fe2+, changing color from red to blue when the electrolysis of Fe2+ is complete.
Note
Reaction 11.34 is the same reaction we used in Chapter 9 to develop our understanding of redox titrimetry.
See Figure 9.40 for the titration curve and for ferroin's color change.
Instrumentation
Controlled-current coulometry normally is carried out using a two-electrode galvanostat, consisting of a working electrode and a counter electrode. The working electrode—often a simple Pt electrode—is also called the generator electrode since it is where the mediator reacts to generate the species that reacts with the analyte. If necessary, the counter electrode is isolated from the analytical solution by a salt bridge or porous frit to prevent its electrolysis products from reacting with the analyte. Alternatively, we can generate the oxidizing agent or the reducing agent externally, and allow it to flow into the analytical solution. Figure 11.33 shows one simple method for accomplishing this. A solution containing the mediator flows into a small-volume electrochemical cell, with the products exiting through separate tubes. Depending upon the analyte, the oxidizing agent or the reducing reagent is selectively delivered to the analytical solution. For example, we can generate Ce4+ using an aqueous solution of Ce3+, directing the Ce4+ that forms at the anode into our sample.
Note
Figure 11.4 shows an example of a manual galvanostat. Although a modern galvanostat uses very different circuitry, you can use Figure 11.4 and the accompanying discussion to understand how we can use the working electrode and the counter electrode to control the current. Figure 11.4 includes an optional reference electrode, but its presence or absence is not important if we are not interested in monitoring the working electrode’s potential.
Figure 11.33 One example of a device for the external generation of oxidizing agents and reducing agents for controlled-current coulometry. A solution containing the mediator flows into a small-volume electrochemical cell. The resulting oxidation products, which form at the anode, flow to the right and may serve as an oxidizing agent. Reduction at the cathode generates a reducing agent.
There are two other crucial needs for controlled-current coulometry: an accurate clock for measuring the electrolysis time, te, and a switch for starting and stopping the electrolysis. An analog clock can record time to the nearest ±0.01 s, but the need to frequently stop and start the electrolysis as we approach the endpoint may result in an overall uncertainty of ±0.1 s. A digital clock allows for a more accurate measurement of time, with an overall uncertainty of ±1 ms being possible. The switch must control both the current and the clock, so that we can make an accurate determination of the electrolysis time.
Coulometric Titrations
A controlled-current coulometric method is sometimes called a coulometric titration because of its similarity to a conventional titration. For example, in the controlled-current coulometric analysis for Fe2+ using a Ce3+ mediator, the oxidation of Fe2+ by Ce4+ (reaction 11.34) is identical to the reaction in a redox titration (reaction 9.15).
There are other similarities between controlled-current coulometry and titrimetry. If we combine equation 11.25 and equation 11.26 and solve for the moles of analyte, NA, we obtain the following equation.
\[N_\ce{A} = \dfrac{i}{nF}× t_\ce{e}\tag{11.35}\]
Compare equation 11.35 to the relationship between the moles of analyte, NA, and the moles of titrant, NT, in a titration
\[N_\ce{A} = N_\ce{T} = M_\ce{T} × V_\ce{T}\]
where MT and VT are the titrant’s molarity and the volume of titrant at the end point. In constant-current coulometry, the current source is equivalent to the titrant and the value of that current is analogous to the titrant’s molarity. Electrolysis time is analogous to the volume of titrant, and te is equivalent to the a titration’s end point. Finally, the switch for starting and stopping the electrolysis serves the same function as a buret’s stopcock.
Note
For simplicity, we are assuming that the stoichiometry between the analyte and titrant is 1:1. The assumption, however, is not important and does not effect our observation of the similarity between controlled-current coulometry and a titration.
11.3.3 Quantitative Applications
Coulometry is used for the quantitative analysis of both inorganic and organic analytes. Examples of controlled-potential and controlled-current coulometric methods are discussed in the following two sections.
Controlled-Potential Coulometry
The majority of controlled-potential coulometric analyses involve the determination of inorganic cations and anions, including trace metals and halides ions. Table 11.8 summarizes several of these methods.
|
analyte |
electrolytic reactiona |
electrode |
|---|---|---|
|
antimony |
Sb(III) + 3e− ⇋ Sb |
Pt |
|
arsenic |
As(III) ⇋ As(V) + 2e− |
Pt |
|
cadmium |
Cd(II) + 2e− ⇋ Cd |
Pt or Hg |
|
cobalt |
Co(II) + 2e− ⇋ Co |
Pt or Hg |
|
copper |
Cu(II) + 2e− ⇋ Cu |
Pt or Hg |
|
halides (X–) |
Ag + X− ⇋ AgX + e− |
Ag |
|
iron |
Fe(II) ⇋ Fe(III) + e− |
Pt |
|
lead |
Pb(II) + 2e− ⇋ Pb |
Pt or Hg |
|
nickel |
Ni(II) + 2e− ⇋ Ni |
Pt or Hg |
|
plutonium |
Pu(III) ⇋ Pu(IV) + e− |
Pt |
|
silver |
Ag(I) + e− ⇋ Ag |
Pt |
|
tin |
Sn(II) + 2e− ⇋ Sn |
Pt |
|
uranium |
U(VI) + 2e− ⇋ U(IV) |
Pt or Hg |
|
zinc |
Zn(II) + 2e− ⇋ Zn |
Pt or Hg |
Source: Rechnitz, G. A. Controlled-Potential Analysis, Macmillan: New York, 1963.
a Electrolytic reactions are written in terms of the change in the analyte’s oxidation state. The actual species in solution depends on the analyte.
The ability to control selectivity by carefully adjusting the working electrode’s potential makes controlled-potential coulometry particularly useful for the analysis of alloys. For example, we can determine the composition of an alloy containing Ag, Bi, Cd, and Sb by dissolving the sample and placing it in a matrix of 0.2 M H2SO4 along with a Pt working electrode and a Pt counter electrode. If we apply a constant potential of +0.40 V versus the SCE, Ag(I) deposits on the electrode as Ag and the other metal ions remain in solution. When electrolysis is complete, we use the total charge to determine the amount of silver in the alloy. By shifting the working electrode’s potential to –0.08 V versus the SCE, we deposit Bi on the working electrode. When the coulometric analysis for bismuth is complete, we determine antimony by shifting the working electrode’s potential to –0.33 V versus the SCE, depositing Sb. Finally, we determine cadmium following its electrodeposition on the working electrode at a potential of –0.80 V versus the SCE.
We also can use controlled-potential coulometry for the quantitative analysis of organic compounds, although the number of applications is significantly less than that for inorganic analytes. One example is the six-electron reduction of a nitro group, –NO2, to a primary amine, –NH2, at a mercury electrode. Solutions of picric acid—also known as 2,4,6-trinitrophenol, or TNP, a close relative of TNT—can be analyzed by reducing it to triaminophenol.
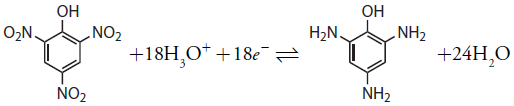
Another example is the successive reduction of trichloroacetate to dichloroacetate, and of dichloroacetate to monochloroacetate
\[\ce{Cl3CCOO-}(aq) + \ce{H3O+}(aq) + 2e^- ⇋ \ce{Cl2HCCOO-}(aq) + \ce{Cl-}(aq) + \ce{H2O}(l)\]
\[\ce{Cl2HCCOO-}(aq) + \ce{H3O+}(aq) + 2e^- ⇋ \ce{ClH2CCOO-}(aq) + \ce{Cl-}(aq) + \ce{H2O}(l)\]
We can analyze a mixture of trichloroacetate and dichloroacetate by selecting an initial potential at which only the more easily reduced trichloroacetate reacts. When its electrolysis is complete, we can reduce dichloroacetate by adjusting the potential to a more negative potential. The total charge for the first electrolysis gives the amount of trichloroacetate, and the difference in total charge between the first electrolysis and the second electrolysis gives the amount of dichloroacetate.
Controlled-Current Coulometry (Coulometric Titrations)
The use of a mediator makes a coulometric titration a more versatile analytical technique than controlled-potential coulometry. For example, the direct oxidation or reduction of a protein at a working electrode is difficult if the protein’s active redox site lies deep within its structure. A coulometric titration of the protein is possible, however, if we use the oxidation or reduction of a mediator to produce a solution species that reacts with the protein. Table 11.9 summarizes several controlled-current coulometric methods based on a redox reaction using a mediator.
| mediator | electrochemically generated reagent and reaction | representative applicationa |
|---|---|---|
| Ag+ | \(\mathrm{Ag^{2+} \textrm{: }Ag^+ ⇋ Ag^{2+} + \mathit{e}^-}\) |
\(\underline{\ce{H2C2O4}(aq)} + \ce{2Ag^2+}(aq) + \ce{2H2O}(l) ⇋ \ce{2CO2}(g) + \ce{2Ag+}(aq) + \ce{2H3O+}(aq)\) |
| Br– | \(\mathrm{Br_2\textrm{: }2Br^- ⇋ Br_2 + 2\mathit{e}^-}\) | \(\underline{\ce{H2S}(aq)} + \ce{Br2}(aq) + \ce{2H2O}(l) ⇋ \ce{S}(s) + \ce{2Br-}(aq) + \ce{2H3O+}(aq)\) |
| Ce3+ | \(\mathrm{Ce^{4+}\textrm{: }Ce^{3+} ⇋ Ce^{4+} + \mathit{e}^-}\) | \(\underline{\ce{Fe(CN)6^4-}(aq)} + \ce{Ce^4+}(aq) ⇋ \ce{Fe(CN)6^3-}(aq) + \ce{Ce^3+}(aq)\) |
| Cl− | \(\mathrm{Cl_2\textrm{: }2Cl^- ⇋ Cl_2 + 2\mathit{e}^-}\) | \(\underline{\ce{Ti(I)}(aq)} + \ce{Cl2}(aq) ⇋ \ce{Ti(III)}(aq) + \ce{2Cl-}(aq)\) |
| Fe3+ | \(\mathrm{Fe^{2+}\textrm{: }Fe^{3+} + \mathit{e}^− ⇋ Fe^{2+}}\) | \(\underline{\ce{Cr2O7^2-}(aq)} + \ce{6Fe^2+}(aq) + \ce{14H3O+}(aq) ⇋ \ce{2Cr^3+}(aq) + \ce{6Fe^3+}(aq) + \ce{21H2O}(l)\) |
| I− | \(\ce{I3-}\textrm{: }\ce{3I-} ⇋ \ce{I3-} + 2e^-\) | \(\underline{\ce{2S2O3^2-}(aq)} + \ce{I3-}(aq) ⇋ \ce{2S4O6^2-}(aq) + \ce{3I-}(aq)\) |
| Mn2+ | \(\mathrm{Mn^{3+}\textrm{: }Mn^{2+} ⇋ Mn^{3+} + \mathit{e}^−}\) | \(\underline{\ce{As(III)}(aq)} + \ce{2Mn^3+}(aq) ⇋ \ce{As(V)}(aq) + \ce{2Mn^2+}(aq)\) |
a The analyte is the underlined species in each reaction.
For an analyte that is not easily oxidized or reduced, we can complete a coulometric titration by coupling a mediator’s oxidation or reduction to an acid–base, precipitation, or complexation reaction involving the analyte. For example, if we use H2O as a mediator, we can generate H3O+ at the anode
\[\ce{6H2O}(l) ⇋ \ce{4H3O+}(aq) + \ce{O2}(g) + 4e^-\]
and generate OH– at the cathode.
\[\ce{2H2O}(l) + 2e^- ⇋ \ce{2OH-}(aq) + \ce{H2}(g)\]
If we carry out the oxidation or reduction of H2O using the generator cell in Figure 11.33, then we can selectively dispense H3O+ or OH– into a solution containing the analyte. The resulting reaction is identical to that in an acid–base titration. Coulometric acid–base titrations have been used for the analysis of strong and weak acids and bases, in both aqueous and non-aqueous matrices. Table 11.10 summarizes several examples of coulometric titrations involving acid–base, complexation, and precipitation reactions.
| type of reaction |
mediator | electrochemically generated reagent and reaction |
representative applicationa |
|---|---|---|---|
| acid–base |
H2O H2O |
\(\mathrm{H_3O^+\textrm{: }6H_2O ⇋ 4H_3O^+ + O_2} + 4e^-\) \(\mathrm{OH^-\textrm{: }2H_2O + 2\mathit{e}^- ⇋ 2OH^- + H_2}\) |
\(\underline{\ce{OH^-}(aq)} + \ce{H3O+}(aq) ⇋ \ce{2H2O}(l)\) \(\underline{\ce{H3O+}(aq)} + \ce{OH-}(aq) ⇋ \ce{2H2O}(l)\) |
| complexation |
HgNH3Y2− Y = EDTA |
\(\mathrm{HY^{3−}\textrm{: }HgNH_3Y^{2−} + NH_4^+ + 2\mathit{e}^− \\ \phantom{HY^{3−}\textrm{: }HgNH_3}⇋ HY^{3−} + Hg + 2NH_3}\) |
\(\underline{\ce{Ca^2+}(aq)} + \ce{HY^3-}(aq) + \ce{H2O}(l) \\ \phantom{\ce{Ca^2+}(aq} ⇋ \ce{CaY^2-}(aq) + \ce{H3O+}(aq)\) |
| precipitation |
Ag Hg Fe(CN)63− |
\(\mathrm{Ag^+\textrm{: }Ag ⇋ Ag^+} + e^-\) \(\mathrm{Hg_2^{2+}\textrm{: }2Hg ⇋ Hg_2^{2+}} + 2e^-\) \(\mathrm{Fe(CN)_6^{4−}\textrm{: }Fe(CN)_6^{3-} + \mathit{e}^− ⇋ Fe(CN)_6^{4−}}\) |
\(\underline{\ce{I-}(aq)} + \ce{Ag+}(aq) ⇋ \ce{AgI}(s)\) \(2\underline{\ce{Cl-}(aq)} + \ce{Hg2^2+}(aq) ⇋ \ce{Hg2Cl2}(s)\) \(3\underline{\ce{Zn^2+}(aq)} + \ce{K+}(aq) + \ce{2Fe(CN)_6^4-}(aq)\\ |
In comparison to a conventional titration, a coulometric titration has two important advantages. The first advantage is that electrochemically generating a titrant allows us to use an unstable reagent. Although we cannot easily prepare and store a solution of a highly reactive reagent, such as Ag2+ or Mn3+, we can generate them electrochemically and use them in a coulometric titration. Second, because it is relatively easy to measure a small quantity of charge, we can use a coulometric titration to determine an analyte whose concentration is too small for a conventional titration.
Quantitative Calculations
The absolute amount of analyte in a coulometric analysis is determined by applying Faraday’s law (equation 11.25), with the total charge given by equation 11.26 or equation 11.27. Example 11.10 shows the calculations for a typical coulometric analysis.
Example 11.10
To determine the purity of a sample of Na2S2O3, a sample is titrated coulometrically using I– as a mediator and I3– as the titrant. A sample weighing 0.1342 g is transferred to a 100-mL volumetric flask and diluted to volume with distilled water. A 10.00-mL portion is transferred to an electrochemical cell along with 25 mL of 1 M KI, 75 mL of a pH 7.0 phosphate buffer, and several drops of a starch indicator solution. Electrolysis at a constant current of 36.45 mA requires 221.8 s to reach the starch indicator endpoint. Determine the sample’s purity.
Solution
As shown in Table 11.9, the coulometric titration of S2O32– with I3– is
\[\ce{2S2O3^2-}(aq) + \ce{3I3-}(aq) ⇋ \ce{S4O6^2-}(aq) + \ce{3I-}(aq)\]
The oxidation of S2O32– to S4O62– requires one electron per S2O32– (n = 1). Combining equation 11.25 and equation 11.26, and solving for the moles and grams of Na2S2O3 gives
\[N_\ce{A}= \dfrac{it_\ce{e}}{nF} = \mathrm{\dfrac{(0.03645\: A)(221.8\: s)}{\left(\dfrac{1\: mol\: e^-}{mol\: Na_2S_2O_3}\right)\left(\dfrac{96487\: C}{mol\: \mathit{e}^-}\right)} = 8.379×10^{−5}\: mol\: Na_2S_2O_3}\]
\[\mathrm{8.379×10^{−5}\: mol\: Na_2S_2O_3 × \dfrac{158.1\: g\: Na_2S_2O_3}{mol\: Na_2S_2O_3} = 0.01325\: g\: Na_2S_2O_3}\]
This is the amount of Na2S2O3 in a 10.00-mL portion of a 100-mL sample; thus, there are 0.1325 grams of Na2S2O3 in the original sample. The sample’s purity, therefore, is
\[\mathrm{\dfrac{0.01325\: g\: Na_2S_2O_3}{0.1342\: g\: sample} × 100 = 98.73\%\: w/w\: Na_2S_2O_3}\]
Note that in using equation 11.25 and equation 11.26, it does not matter whether S2O32– is oxidized at the working electrode or is oxidized by I3–.
Exercise 11.7
To analyze a brass alloy, a 0.442-g sample is dissolved in acid and diluted to volume in a 500-mL volumetric flask. Electrolysis of a 10.00-mL sample at –0.3 V versus a SCE reduces Cu2+ to Cu, requiring a total charge of 16.11 C. Adjusting the potential to –0.6 V versus a SCE and completing the electrolysis requires 0.442 C to reduce Pb2+ to Pb. Report the %w/w Cu and Pb in the alloy.
Click here to review your answer to this exercise.
The best way to appreciate the theoretical and practical details discussed in this section is to carefully examine a typical analytical method. Although each method is unique, the following description of the determination of Cr2O72– provides an instructive example of a typical procedure. The description here is based on Bassett, J.; Denney, R. C.; Jeffery, G. H.; Mendham, J. Vogel’s Textbook of Quantitative Inorganic Analysis, Longman: London, 1978, p. 559–560.
Representative Method 11.2: Determination of Dichromate by a Coulometric Redox Titration
Description of the Method
The concentration of Cr2O72– in a sample is determined by a coulometric redox titration using Fe3+ as a mediator and electrogenerated Fe2+ as the titrant. The endpoint of the titration is determined potentiometrically.
Procedure
The electrochemical cell consists of a Pt working electrode and a Pt counter electrode placed in separate cells connected by a porous glass disk. Fill the counter electrode’s cell with 0.2 M Na2SO4, keeping the level above that of the solution in the working electrode’s cell. Connect a platinum electrode and a tungsten electrode to a potentiometer so that you can measure the working electrode’s potential during the analysis. Prepare a mediator solution of approximately 0.3 M NH4Fe(SO4)2. Add 5.00 mL of sample, 2 mL of 9 M H2SO4, and 10–25 mL of the mediator solution to the working electrode’s cell, and add distilled water as needed to cover the electrodes. Bubble pure N2 through the solution for 15 min to remove any O2 that might be present. Maintain the flow of N2 during the electrolysis, turning if off momentarily when measuring the potential. Stir the solution using a magnetic stir bar. Adjust the current to 15–50 mA and begin the titration. Periodically stop the titration and measure the potential. Construct a titration curve of potential versus time and determine the time needed to reach the equivalence point.
Questions
1. Is the platinum working electrode the cathode or the anode?
Reduction of Fe3+ to Fe2+ occurs at the working electrode, making it the cathode in this electrochemical cell.
2. Why is it necessary to remove dissolved oxygen by bubbling N2 through the solution?
Any dissolved O2 will oxidize Fe2+ back to Fe3+, as shown by the following reaction.
\[\ce{4Fe^2+}(aq) + \ce{O2}(aq) + \ce{4H3O+}(aq) ⇋ \ce{4Fe^3+}(aq) + \ce{6H2O}(l)\]
To maintain current efficiency, all the Fe2+ must react with Cr2O72–. The reaction of Fe2+ with O2 means that more of the Fe3+ mediator is needed, increasing the time to reach the titration’s endpoint. As a result, we report the presence of too much Cr2O72–.
3. What effect is there if the NH4Fe(SO4)2 is contaminated with trace amounts of Fe2+? How can you compensate for this source of Fe2+?
There are two sources of Fe2+: that generated from the mediator and that present as an impurity. Because the total amount of Fe2+ reacting with Cr2O72– remains unchanged, less Fe2+ must be generated from the mediator. This decreases the time needed to reach the titration's end point. Because the apparent current efficiency is greater than 100%, and the reported concentration of Cr2O72– is too small. We can remove trace amount of Fe2+ from the mediator solution by adding H2O2 and heating at 50–70oC until the evolution of O2 ceases, converting the Fe2+ to Fe3+. Alternatively, we can complete a blank titration to correct for any impurities of Fe2+ in the mediator.
4. Why is the level of solution in the counter electrode’s cell maintained above the solution level in the working electrode’s cell?
This prevents the solution containing the analyte from entering the counter electrode’s cell. The oxidation of H2O at the counter electrode produces O2, which can react with the Fe2+ generated at the working electrode or the Cr3+ resulting from the reaction of Fe2+ and Cr2O72–. In either case, the result is a positive determinate error.
11.3.4 Characterization Applications
One useful application of coulometry is determining the number of electrons involved in a redox reaction. To make the determination, we complete a controlled-potential coulometric analysis using a known amount of a pure compound. The total charge at the end of the electrolysis is used to determine the value of n using Faraday’s law (equation 11.25).
Example 11.11
A 0.3619-g sample of tetrachloropicolinic acid, C6HNO2Cl4, is dissolved in distilled water, transferred to a 1000-mL volumetric flask, and diluted to volume. An exhaustive controlled-potential electrolysis of a 10.00-mL portion of this solution at a spongy silver cathode requires 5.374 C of charge. What is the value of n for this reduction reaction?
Solution
The 10.00-mL portion of sample contains 3.619 mg, or 1.39 × 10–5 mol of tetrachloropicolinic acid. Solving equation 11.25 for n and making appropriate substitutions gives
\[\begin{align}
n &= \dfrac{Q}{FN_\ce{A}}= \mathrm{\dfrac{5.274\: C}{(96478\: C / mol\:\mathit{e}^−)(1.39×10^{−5}\: mol\: C_6HNO_2Cl_4)}}\\
&= \mathrm{4.01\: mol\: \mathit{e}^− / mol\: C_6HNO_2Cl_4}
\end{align}\]
Thus, reducing a molecule of tetrachloropicolinic acid requires four electrons. The overall reaction, which results in the selective formation of 3,6-dichloropicolinic acid, is
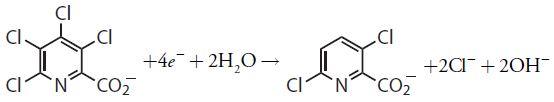
11.3.5 Evaluation
Scale of Operation
A coulometric method of analysis can be used to analyze a small absolute amount of an analyte. In controlled-current coulometry, for example, the moles of analyte consumed during an exhaustive electrolysis is given by equation 11.35. An electrolysis using a constant current of 100 μA for 100 s, for example, consumes only 1 × 10–7 mol of analyte if n = 1. For an analyte with a molecular weight of 100 g/mol, 1 × 10–7 mol of analyte corresponds to only 10 μg. The concentration of analyte in the electrochemical cell, however, must be sufficient to allow an accurate determination of the endpoint. When using a visual end point, the smallest concentration of analyte that can be determined by a coulometric titration is approximately 10–4 M. As is the case for a conventional titration, a coulometric titration using a visual end point is limited to major and minor analytes. A coulometric titration to a preset potentiometric endpoint is feasible even if the analyte’s concentration is as small as 10–7 M, extending the analysis to trace analytes.12
Note
See Figure 3.5 to review the meaning of major, minor, and and trace analytes.
Accuracy
When using controlled-current coulometry accuracy is determined by the current efficiency, by the accuracy with which we can measure current and time, and by the accuracy of the end point. The maximum measurement errors for current and time are about ±0.01% and ±0.1%, respectively. The maximum end point error for a coulometric titration is at least as good as that for a conventional titration, and is often better when using small quantities of reagents. Together, these measurement errors suggest that an accuracy of 0.1%–0.3% is feasible. The limiting factor in many analyses, therefore, is current efficiency. A current efficiency of greater than 99.5% is fairly routine, and it often exceeds 99.9%.
In controlled-potential coulometry, accuracy is determined by current efficiency and by the determination of charge. If the sample is free of interferents that are easier to oxidize or reduce than the analyte, a current efficiency of greater than 99.9% is routine. When an interferent is present, it can often be eliminated by applying a potential where the exhaustive electrolysis of the interferents is possible without the simultaneous electrolysis of the analyte. Once the interferent has been removed the potential can be switched to a level where electrolysis of the analyte is feasible. The limiting factor in the accuracy of many controlled-potential coulometric methods of analysis is the determination of charge. With electronic integrators the total charge can be determined with an accuracy of better than 0.5%.
If we cannot obtain an acceptable current efficiency, an electrogravimetic analysis may be possible if the analyte—and only the analyte—forms a solid deposit on the working electrode. In this case the working electrode is weighed before beginning the electrolysis and reweighed when the electrolysis is complete. The difference in the electrode’s weight gives the analyte’s mass.
Precision
Precision is determined by the uncertainties in measuring current, time, and the endpoint in controlled-current coulometry or of charge in controlled-potential coulometry. Precisions of ±0.1–0.3% are routinely obtained in coulometric titrations, and precisions of ±0.5% are typical for controlled-potential coulometry.
Sensitivity
For a coulometric method of analysis the calibration sensitivity is equivalent to nF in equation 11.25. In general, a coulometric method is more sensitive if the analyte’s oxidation or reduction involves a larger value of n.
Selectivity
Selectivity in controlled-potential and controlled-current coulometry is improved by carefully adjusting solution conditions and by properly selecting the electrolysis potential. In controlled-potential coulometry, the potential is fixed by the potentiostat, and in controlled-current coulometry the potential is determined by the redox reaction with the mediator. In either case, the ability to control the electrolysis potential affords some measure of selectivity. By adjusting pH or adding a complexing agent, it may be possible to shift the potential at which an analyte or interferent undergoes oxidation or reduction. For example, the standard-state reduction potential for Zn2+ is –0.762 V versus the SHE. If we add a solution of NH3, forming Zn(NH3)42, the standard state potential shifts to –1.04 V. This provides an additional means for controlling selectivity when an analyte and interferent undergo electrolysis at similar potentials.
Time, Cost, and Equipment
Controlled-potential coulometry is a relatively time consuming analysis, with a typical analysis requiring 30–60 min. Coulometric titrations, on the other hand, require only a few minutes, and are easily adapted for automated analysis. Commercial instrumentation for both controlled-potential and controlled-current coulometry is available, and is relatively inexpensive. Low cost potentiostats and constant-current sources are available for approximately $1000.