10.8: Spectroscopy Based on Scattering
- Page ID
- 5615
The blue color of the sky during the day and the red color of the sun at sunset result from the scattering of light by small particles of dust, molecules of water, and other gases in the atmosphere. The efficiency of a photon’s scattering depends on its wavelength. We see the sky as blue during the day because violet and blue light scatter to a greater extent than other, longer wavelengths of light. For the same reason, the sun appears red at sunset because red light is less efficiently scattered and is more likely to pass through the atmosphere than other wavelengths of light. The scattering of radiation has been studied since the late 1800s, with applications beginning soon thereafter. The earliest quantitative applications of scattering, which date from the early 1900s, used the elastic scattering of light by colloidal suspensions to determine the concentration of colloidal particles.
10.8.1 Origin of Scattering
If we send a focused, monochromatic beam of radiation with a wavelength λ through a medium of particles with dimensions <1.5λ, the radiation scatters in all directions. For example, visible radiation of 500 nm is scattered by particles as large as 750 nm in the longest dimension. Two general categories of scattering are recognized. In elastic scattering, radiation is first absorbed by the particles and then emitted without undergoing change in the radiation’s energy. When the radiation emerges with a change in energy, the scattering is said to be inelastic. Only elastic scattering is considered in this text.
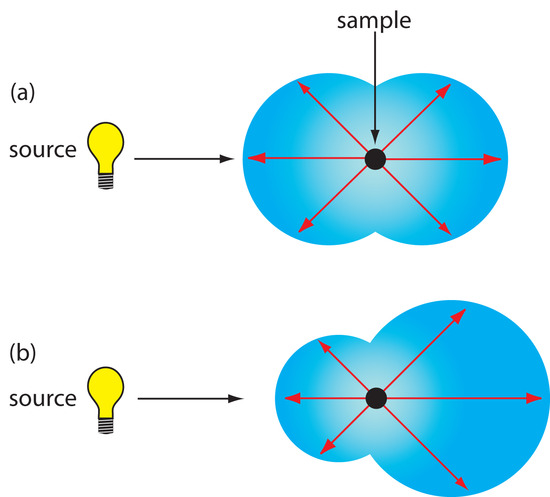
Elastic scattering is divided into two types: Rayleigh, or small-particle scattering, and large-particle scattering. Rayleigh scattering occurs when the scattering particle’s largest dimension is less than 5% of the radiation’s wavelength. The intensity of the scattered radiation is proportional to its frequency to the fourth power, ν4—accounting for the greater scattering of blue light than red light—and is symmetrically distributed (Figure 10.63a). For larger particles, scattering increases in the forward direction and decreases in the backwards direction as the result of constructive and destructive interferences (Figure 10.63b).
Figure 10.63 Distribution of radiation for (a) Rayleigh, or small-particle scattering, and (b) large-particle scattering.
10.8.2 Turbidimetry and Nephelometry
Turbidimetry and nephelometry are two techniques based on the elastic scattering of radiation by a suspension of colloidal particles. In turbidimetry the detector is placed in line with the source and the decrease in the radiation’s transmitted power is measured. In nephelometry scattered radiation is measured at an angle of 90o to the source. The similarity of turbidimetry to absorbance and of nephelometry to fluorescence is evident in the instrumental designs shown in Figure 10.64. In fact, turbidity can be measured using a UV/Vis spectrophotometer and a spectrofluorimeter is suitable for nephelometry.
Figure 10.64 Schematic diagrams for (a) a turbimeter, and (b) a nephelometer.
Turbidimetry or Nephelometry?
When developing a scattering method the choice of using turbidimetry or nephelometry is determined by two factors. The most important consideration is the intensity of the scattered radiation relative to the intensity of the source’s radiation. If the solution contains a small concentration of scattering particles the intensity of the transmitted radiation, IT, is approximately the same as the intensity of the source’s radiation, I0. As we learned earlier in the section on molecular absorption, there is substantial uncertainty in determining a small difference between two intense signals. For this reason, nephelometry is a more appropriate choice for samples containing few scattering particles. Turbidimetry is a better choice when the sample contains a high concentration of scattering particles.
A second consideration in choosing between turbidimetry and nephelometry is the size of the scattering particles. For nephelometry, the intensity of scattered radiation at 90o increases when the particles are small and Rayleigh scattering is in effect. For larger particles, as shown in Figure 10.63, the intensity of scattering is diminished at 90o. When using an ultraviolet or visible source of radiation, the optimum particle size is 0.1–1 μm. The size of the scattering particles is less important for turbidimetry where the signal is the relative decrease in transmitted radiation. In fact, turbidimetric measurements are still feasible even when the size of the scattering particles results in an increase in reflection and refraction, although a linear relationship between the signal and the concentration of scattering particles may no longer hold.
Determining Concentration by Turbidimetry
In turbidimetry, the measured transmittance, \(T\), is the ratio of the intensity of source radiation transmitted by the sample, \(I_T\), to the intensity of source radiation transmitted by a blank, \(I_0\).
\[T = \dfrac{I_T}{ I_0}\]
The relationship between transmittance and the concentration of the scattering particles is similar to that given by Beer’s law:
\[– \log{T} = k\,b\,C \tag{10.32}\]
where
- \(C\) is the concentration of the scattering particles in mass per unit volume (w/v),
- \(b\) is the pathlength, and
- \(k\) is a constant that depends on several factors, including the size and shape of the scattering particles and the wavelength of the source radiation.
As with Beer’s law, equation 10.32 may show appreciable deviations from linearity. The exact relationship is established by a calibration curve prepared using a series of standards containing known concentrations of analyte.
Determining Concentration by Nephelometry
In nephelometry the relationship between the intensity of scattered radiation, IS, and the concentration of scattering particles is
\[I_\ce{S} = k_\ce{S}I_0C\tag{10.33}\]
where kS is an empirical constant for the system and I0 is the source radiation’s intensity. The value of kS is determined from a calibration curve prepared using a series of standards containing known concentrations of analyte.
Selecting a Wavelength for the Incident Radiation
The choice of wavelength is based primarily on the need to minimize potential interferences. For turbidimetry, where the incident radiation is transmitted through the sample, a monochromator or filter allow us to avoid wavelengths that are absorbed by the sample. For nephelometry, the absorption of incident radiation is not a problem unless it induces fluorescence from the sample. With a nonfluorescent sample there is no need for wavelength selection, and a source of white light may be used as the incident radiation. For both techniques, other considerations in choosing a wavelength including the effect of wavelength on scattering intensity, the transducer’s sensitivity, and the source’s intensity. For example, many common photon transducers are more sensitive to radiation at 400 nm than at 600 nm.
Preparing the Sample for Analysis
Although equation 10.32 and equation 10.33 relate scattering to the concentration of scattering particles, the intensity of scattered radiation is also influenced by the particle’s size and shape. Samples containing the same number of scattering particles may show significantly different values for -logT or IS, depending on the average diameter of the particles. For a quantitative analysis, therefore, it is necessary to maintain a uniform distribution of particle sizes throughout the sample and between samples and standards.
Most turbidimetric and nephelometric methods rely on precipitation to form the scattering particles. As we learned in Chapter 8, the properties of a precipitate are determined by the conditions under which it forms. To maintain a reproducible distribution of particle sizes between samples and standards, it is necessary to control parameters such as the concentration of reagents, the order of adding reagents, the pH and temperature, the agitation or stirring rate, the ionic strength, and the time between the precipitate’s initial formation and the measurement of transmittance or scattering. In many cases a surface-active agent—such as glycerol, gelatin, or dextrin—is added to stabilize the precipitate in a colloidal state and to prevent the coagulation of the particles.
Applications
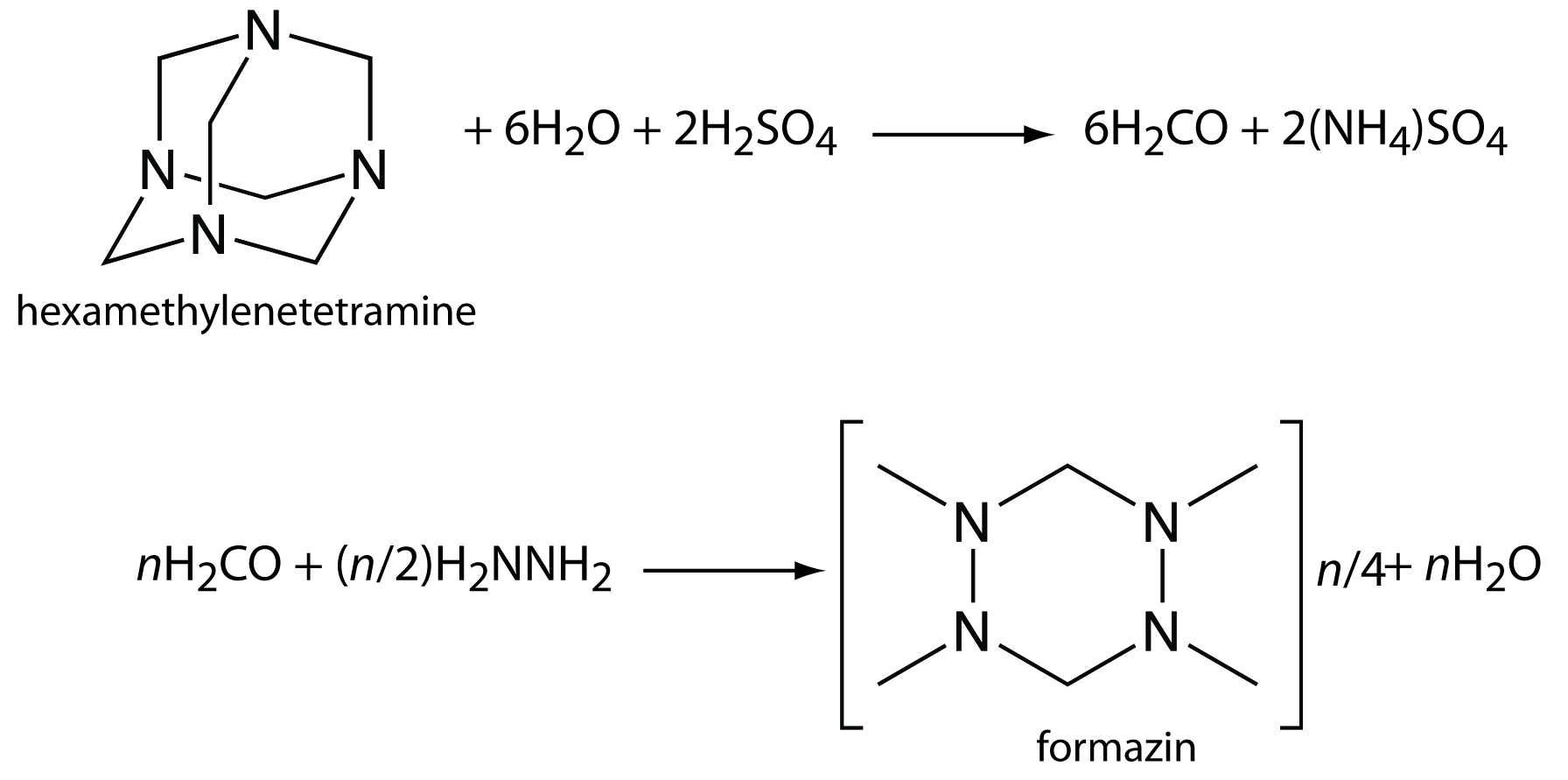
Turbidimetry and nephelometry are widely used to determine the clarity of water, beverages, and food products. For example, a nephelometric determination of the turbidity of water compares the sample’s scattering to the scattering of a set of standards. The primary standard for measuring turbidity is formazin, which is an easily prepared, stable polymer suspension (Figure 10.65).20 Formazin prepared by mixing a 1 g/100 mL solution of hydrazine sulfate, N2H4•H2SO4, with a 10 g/100 mL solution of hexamethylenetetramine produces a suspension that is defined as 4000 nephelometric turbidity units (NTU). A set of standards with NTUs between 0 and 40 is prepared and used to construct a calibration curve. This method is readily adapted to the analysis of the clarity of orange juice, beer, and maple syrup.
Figure 10.65 Scheme for preparing formazin for use as a turbidity standard.
A number of inorganic cations and anions can be determined by precipitating them under well-defined conditions and measuring the transmittance or scattering of radiation from the precipitated particles. The transmittance or scattering, as given by equation 10.32 or equation 10.33 is proportional to the concentration of the scattering particles, which, in turn, is related by the stoichiometry of the precipitation reaction to the analyte’s concentration. Examples of analytes that have been determined in this way are listed in Table 10.15.
|
analyte |
precipitant |
precipitate |
|---|---|---|
| Ag+ | NaCl | AgCl |
| Ca2+ | Na2C2O4 | CaC2O4 |
| Cl– | AgNO3 | AgCl |
| CN– | AgNO3 | AgCN |
| CO32– | BaCl2 | BaCO3 |
| F– | CaCl2 | CaF2 |
| SO42– | BaCl2 | BaSO4 |
Note
The best way to appreciate the theoretical and practical details discussed in this section is to carefully examine a typical analytical method. Although each method is unique, the following description of the determination of sulfate in water provides an instructive example of a typical procedure. The description here is based on Method 4500–SO42––C in Standard Methods for the Analysis of Water and Wastewater, American Public Health Association: Washington, D. C. 20th Ed., 1998.
Representative Method 10.5
Turbidimetric Determination of Sulfate in Water
Description of Method
Adding BaCl2 to an acidified sample precipitates SO42– as BaSO4. The concentration of SO42– may be determined either by turbidimetry or by nephelometry using an incident source of radiation of 420 nm. External standards containing know concentrations of SO42– are used to standardize the method.
Procedure
Transfer a 100-mL sample to a 250-mL Erlenmeyer flask along with 20.00 mL of a buffer. For samples containing >10 mg SO42–/L, the buffer contains 30 g of MgCl2•6H2O, 5 g of CH3COONa•3H2O, 1.0 g of KNO3, and 20 mL of glacial CH3COOH per liter. The buffer for samples containing <10 mg SO42–/L is the same except for the addition of 0.111 g of Na2SO4 per L.
Place the sample and the buffer on a magnetic stirrer operated at the same speed for all samples and standards. Add a spoonful of 20–30 mesh BaCl2, using a measuring spoon with a capacity of 0.2–0.3 mL, to precipitate the SO42– as BaSO4. Begin timing when the BaCl2 is added and stir the suspension for 60 ± 2 s. Measure the transmittance or scattering intensity 5.0± 0.5 min after the end of stirring.
Prepare a calibration curve over the range 0–40 mg SO42–/L by diluting a 100-mg SO42–/L standard. Treat the standards using the procedure described above for the sample. Prepare a calibration curve and use it to determine the amount of sulfate in the sample.
Questions
1. What is the purpose of the buffer?
If the precipitate’s particles are too small, IT may be too small to measure reliably. Because rapid precipitation favors the formation of microcrystalline particles of BaSO4, we use conditions that favor precipitate growth over nucleation. The buffer’s high ionic strength and its acidity favors precipitate growth and prevents the formation of microcrystalline BaSO4.
2. Why is it important to use the same stirring rate and time for the samples and standards?
How fast and how long we stir the sample after adding BaCl2 influence the size of the precipitate’s particles.
3. Many natural waters have a slight color due to the presence of humic and fulvic acids, and may contain suspended matter (Figure 10.66). Explain why these might interfere with the analysis for sulfate. For each interferent, suggest a method for minimizing its effect on the analysis.
Suspended matter in the sample contributes to the scattering, resulting in a positive determinate error. We can eliminate this interference by filtering the sample prior to its analysis. A sample that is colored may absorb some of the source’s radiation, leading to a positive determinate error. We can compensate for this interference by taking a sample through the analysis without adding BaCl2. Because no precipitate forms, we can use the transmittance of this sample blank to correct for the interference.
4. Why is Na2SO4 added to the buffer for samples containing <10 mg SO42–/L?
The uncertainty in a calibration curve is smallest near its center. If a sample has a high concentration of SO42–, we can dilute it so that its concentration falls near the middle of the calibration curve. For a sample with a small concentration of SO42–, the buffer increases the concentration of sulfate by
\[\mathrm{\dfrac{0.111\: g\: Na_2SO_4}{L} × \dfrac{96.06\: g\: SO_4^{2−}}{142.04\: g\: Na_2SO_4} × \dfrac{1000\: mg}{g} × \dfrac{20.00\: mL}{250.0\: mL} = \dfrac{6.00\: mg\: SO_4^{2−}}{L}}\]
After using the calibration curve to determine the amount of sulfate in the sample, subtracting 6.00 mg SO42–/L corrects the result.
Figure 10.66 Waterfall on the River Swale in Richmond, England. The river, which flows out of the moors in the Yorkshire Dales, is brown in color as the result of organic matter that leaches from the peat found in the moors.
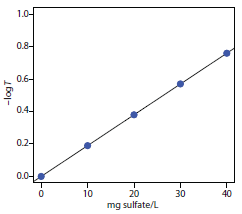
Example 10.13
To evaluate the method described in Representative Method 10.5, a series of external standard was prepared and analyzed, providing the results shown in the following table.
| mg SO42–/L | transmittance |
|
0.00 10.00 20.00 30.00 40.00 |
1.00 0.646 0.417 0.269 0.174 |
Analysis of a 100.0-mL sample of a surface water gives a transmittance of 0.538. What is the concentration of sulfate in the sample?
Solution
Linear regression of -logT versus concentration of SO42– gives a standardization equation of
\[−\log T= \mathrm{−1.04×10^{−5} + 0.0190 × \dfrac{mg\: SO_4^{2−}}{L}}\]
Substituting the sample’s transmittance into the calibration curve’s equation gives the concentration of sulfate in sample as 14.2 mg SO42–/L.
