4.7: Detection Limits
- Page ID
- 5748
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The International Union of Pure and Applied Chemistry (IUPAC) defines a method’s detection limit as the smallest concentration or absolute amount of analyte that has a signal significantly larger than the signal from a suitable blank.12 Although our interest is in the amount of analyte, in this section we will define the detection limit in terms of the analyte’s signal. Knowing the signal you can calculate the analyte’s concentration, CA, or the moles of analyte, nA, using the equations
\[S_\ce{A} = k_\ce{A}C_\ce{A} \hspace{20px} \ce{or} \hspace{20px} S_\ce{A} = k_\ce{A}n_\ce{A}\]
where k is the method’s sensitivity. (See Chapter 3 for a review of these equations.)
Let’s translate the IUPAC definition of the detection limit into a mathematical form by letting Smb represent the average signal for a method blank, and letting σmb represent the method blank’s standard deviation. The null hypothesis is that the analyte is not present in the sample, and the alternative hypothesis is that the analyte is present in the sample. To detect the analyte, its signal must exceed Smb by a suitable amount; thus,
\[(S_\ce{A})_\ce{DL} = S_\ce{mb} + zσ_\ce{mb}\tag{4.24}\]
where (SA)DL is the analyte’s detection limit.
Note
If σmb is not known, we can replace it with smb; equation 4.24 then becomes
\[(S_\ce{A})_\ce{DL} = S_\ce{mb} + \dfrac{ts_\ce{mb}}{\sqrt{n}}\]
You can make similar adjustments to other equations in this section. See, for example, Kirchner, C. J. “Estimation of Detection Limits for Environmental Analytical Procedures,” in Currie, L. A. (ed) Detection in Analytical Chemistry: Importance, Theory, and Practice; American Chemical Society: Washington, D. C., 1988.
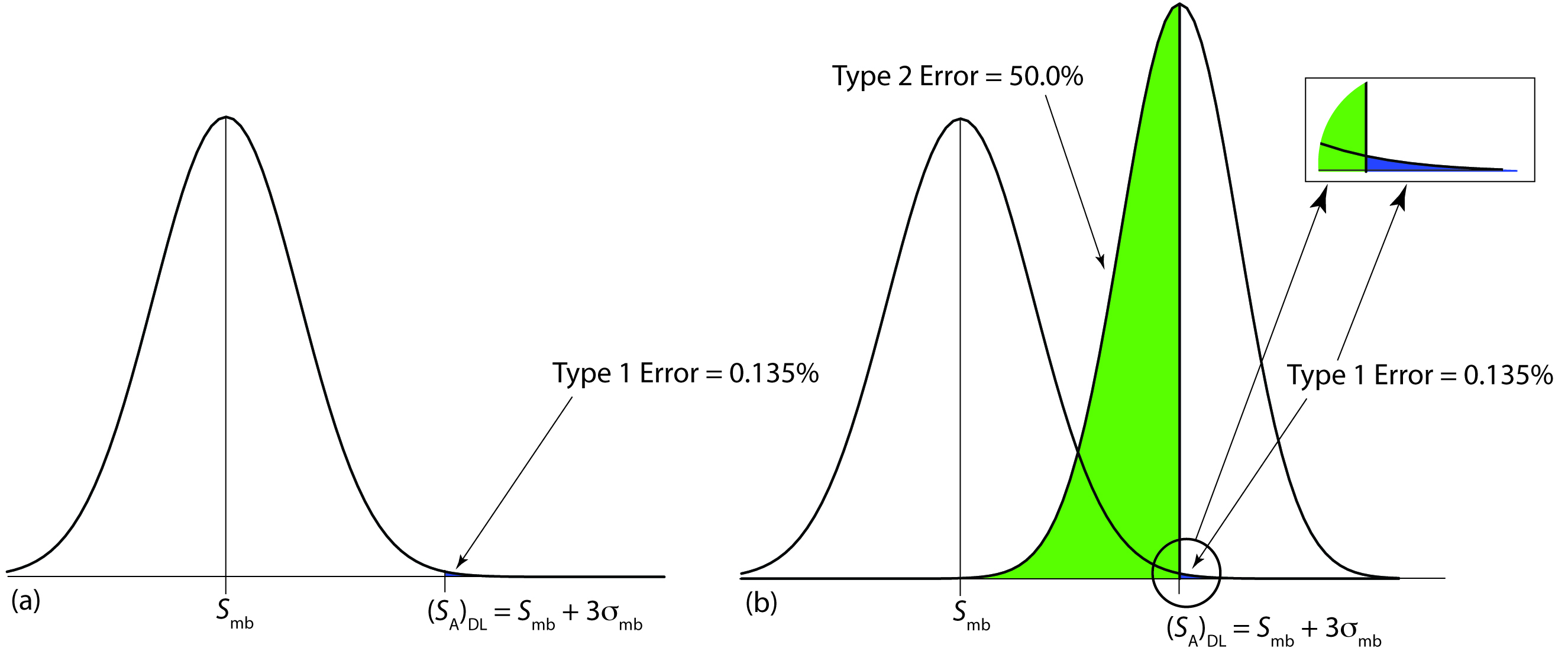
The value we choose for z depends on our tolerance for reporting the analyte’s concentration even though it is absent from the sample (a type 1 error). Typically, z is set to three, which, from Appendix 3, corresponds to a probability, α, of 0.00135. As shown in Figure 4.16a, there is only a 0.135% probability of detecting the analyte in a sample that actually is analyte-free.
A detection limit also is subject to a type 2 error in which we fail to find evidence for the analyte even though it is present in the sample. Consider, for example, the situation shown in Figure 4.16b where the signal for a sample containing the analyte is exactly equal to (SA)DL. In this case the probability of a type 2 error is 50% because half of the signals arising from such samples are below the detection limit. We will correctly detect the analyte at the IUPAC detection limit only half the time. The IUPAC definition for the detection limit indicates the smallest signal for which we can say, at a significance level of α, that an analyte is present in the sample. Failing to detect the analyte does not imply that it is not present in the sample.
The detection limit is often represented, particularly when discussing public policy issues, as a distinct line separating detectable concentrations of analytes that concentrations that cannot be detected. This use of a detection limit is incorrect.13 As suggested by Figure 4.16, for concentrations of analyte near the detection limit there is a high probability of failing to detect the analyte.
Figure 4.16 Normal distribution curves showing the probability of type 1 and type 2 errors for the IUPAC detection limit. (a) The normal distribution curve for the method blank, with Smb = 0 and σmb = 1. The minimum detectable signal for the analyte, (SA)DL, has a type 1 error of 0.135%. (b) The normal distribution curve for the analyte at its detection limit, (SA)DL = 3, is superimposed on the normal distribution curve for the method blank. The standard deviation for the analyte’s signal, σA, is 0.8, The area in green represents the probability of a type 2 error, which is 50%. The inset shows, in blue, the probability of a type 1 error, which is 0.135%.
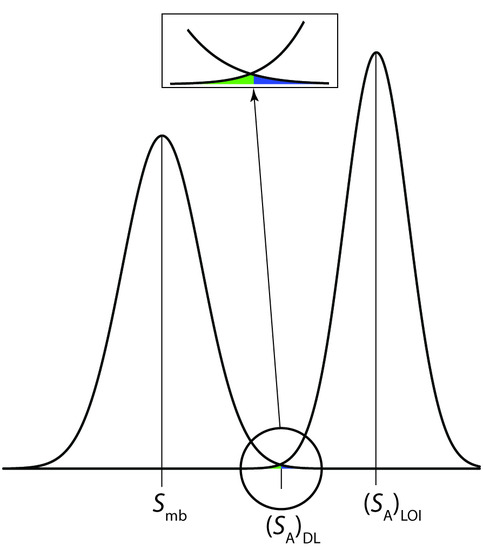
An alternative expression for the detection limit, the limit of identification, minimizes both type 1 and type 2 errors.14 The analyte’s signal at the limit of identification, (SA)LOI, includes an additional term, zσA, to account for the distribution of the analyte’s signal.
\[(S_\ce{A})_\ce{LOI} = (S_\ce{A})_\ce{DL} +zσ_\ce{A} = S_\ce{mb} + zσ_\ce{mb} + zσ_\ce{A}\]
As shown in Figure 4.17, the limit of identification provides an equal probability for type 1 and type 2 errors at the detection limit. When the analyte’s concentration is at its limit of identification, there is only a 0.135% probability that its signal will be indistinguishable from that of the method blank.
Figure 4.17 Normal distribution curves for a method blank and for a sample at the limit of identification: Smb = 0; σmb = 1; σA = 0.8; and (SA)LOI = 0 + 3 × 1 + 3 × 0.8 = 5.4. The inset shows that the probability of a type 1 error (0.135%) is the same as the probability of a type 2 error (0.135%).
The ability to detect the analyte with confidence is not the same as the ability to report with confidence its concentration, or to distinguish between its concentration in two samples. For this reason the American Chemical Society’s Committee on Environmental Analytical Chemistry recommends the limit of quantitation, (SA)LOQ.15
\[(S_\ce{A})_\ce{LOQ} = S_\ce{mb} + 10σ_\ce{mb}\]