Extra Credit 33

2.60, 9.3, 9.27, 10.2, 11.17, 12.9, 13.12, 14.15, 2.71, 9.10

Practice Problems

2.60

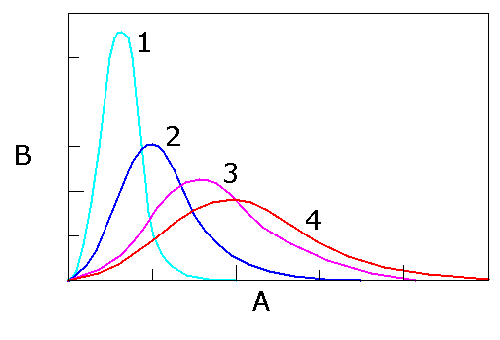
(a) The below graph displays various Maxwell-Boltzmann distributions for the same compound. The following questions correspond to this graph.

1) What does axis A refer to? What does axis B refer to?

2) Which distribution is at the highest temperature? Which is at the lowest temperature? Explain.

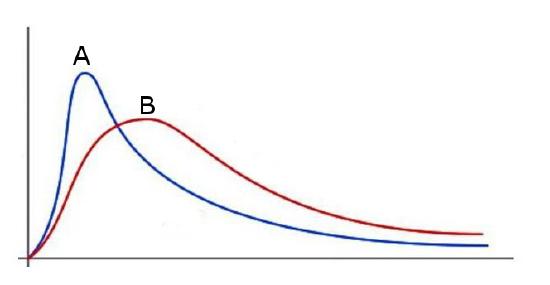
(b) The below graph displays the Maxwell-Boltzmann distributions of two different gases at 298K. One is oxygen gas and the other is nitrogen gas. Identify which distribution corresponds to which compound. Explain how you came to your conclusions.

2.71

It's your birthday and you want to treat yourself. Recently, your mom gave you some magical marbles, 3 cm wide, that exhibit random molecular motion. You decide to fill a cubic gift box with 20 of them because that's the sort of thing that makes you happy. You're having a birthday party later and invite your physicist friend. When she arrives, she inspects the box and she tells you that the mean free path of the marbles atoms is 50 cm. How could you confirm or deny her statement using materials in your house?

9.3

The following elementary reaction occurs:

\[2A + B \rightarrow C\]

Determine the reaction constant when [A] = .02 M and [B] = .1 M. At these concentrations, the reaction velocity is .3 mol L^-1 s^-1. What is the reaction order?

9.10

The following reaction is observed and the concentrations of A are taken over time. What is the reaction order in A? What is k for this reaction?

\[ A \rightarrow P \]

t	[A]
0	2
10	1
30	.5

9.27

A certain reaction takes 20 minutes at 298K and 10 minutes at 308K. What is the activation energy of this reaction?

10.2

You and your friend decide to study enzyme, which catalyzes a reaction in the following simplified scheme:

\[ E + S \xrightarrow[ ]{k_1} ES \xrightarrow[ ]{k_2} E + P \]

You guys divide up the work. Your friend finds that the enzyme substrate complex is generated at a constant rate of 5 mol L^-1 s^-1

You decide to find the rate of enzyme substrate complex dissociation. You collect the following data.

t (s)	[ES] (M)
0	148
10	54.6
30	7.39

What is the order of this reaction? What is k? At what concentration of ES would a steady-state approximation be appropriate?

11.17

You've just helped your 5-year-old child make a small 1 kg solar-powered cart. But that's not enough for you. You want to take your child to the next level. So you ask your child to calculate the number of photons required for the cart to move at 5 m/s. How will your child calculate this?

Although sunlight is composed of different kinds of light electromagnetic radiation, assume that these photons all have a wavelength of 280 nm. Assume that all thermal energy is converted to kinetic energy.

12.9

Consider HCl. Draw the bonding orbitals of this molecule as a) a purely covalent interaction b) a purely ionic interaction and c) as a polar interaction. Explain how the wave functions of each of these scenarios differ.

13.12

Suppose you have 3 moles of bromine gas at room temperature in some container. At what pressure do the bromine atoms occupy 50% of the volume of the container? A table on this page might help.

14.15

You've discovered a new diatomic molecule in the atmosphere and after some experimentation you find its bond length to be \(3 \AA \). You also find that its reduced mass is \( 1.5 \times 10^{-26} kg \). You're having trouble detecting the \( J = 4 \rightarrow 5 \) energy transition. How much energy should be supplied to the molecule to make sure you observe this transition?

Solutions

2.60

(a 1) The Maxwell-Boltzmann distribution describes the distribution of velocities among a fixed number of particles. Axis A refers to the velocity of particles. Axis B refers to the number of particles at some given velocity.

(a 2) Here is a form of the Maxwell-Boltzmann distribution function:

\[f(v)=4\pi v^2 \left (\dfrac{m}{2\pi k_b T} \right)^{3/2}exp\left [\frac{-mv^2}{2k_bT}\right] \label{2}\]

The distribution marked 4 is at the highest temperature, while the distribution marked 1 is at the lowest temperature.

Aside from velocity, one can see that two other variables exist: temperature and mass. Since the distributions shown on the graph are all describing the same compound, the mass of the particle is fixed among the distributions. Therefore, what causes differences in the distributions are changes in temperature.
Two explanations can be given here: mathematical and physical.

Mathematical: Given the nature of the equation, one can see that as temperature increases, the resultant f(v) values generally decrease and become more spread out and visa versa. Since the number of particles described with the distribution does not change, they must all integrate to the same number - i.e. the area underneath each curve must be equivalent.

Physical: Temperature is directly proportional to the average kinetic energy of all particles in a system. Additionally, kinetic energy is directly proportional to velocity. Therefore, temperature is directly proportional to velocity. So, as temperature increases, the average velocity must also increase. Distribution 4 has the highest average velocity, while distribution 1 has the lowest average velocity.

(b) Distribution B corresponds to N_{2 (g)} while distribution A corresponds to O_{2 (g)}.

This graph displays the distribution of two different compounds at the same temperature. Again, a mathematical or physical approach can be taken.

Mathematical: Using the equation, one can see that as mass increases, the resultant f(v) values generally decrease and become more spread out.

Physical: More energy is required to move a more massive object. Given that these particles are moving around at the same ambient thermal energy (i.e. same temperature) and that N₂ is less massive than O₂, N₂ molecules will have a higher average velocity than O₂ will.

2.71

The formula for mean-free path is:

\[ \lambda = \frac{V}{\sqrt{2} \pi d^{2} N} \]

In our case:

purported \( \lambda \) = 50 cm

N = 20 marbles

d = 3 cm

So, the only variable left is volume. Luckily, the volume of a box is easily measured with a ruler. First solve for volume, then confirm that the calculated volume is the true volume of the box.

\[ 50 = \frac{V}{\sqrt{2} \pi 10^{2}20} \]

V = 66643 \( cm^{3} \)

Since the gift box is a cube, the sides would have to be 40.5 cm each.

9.3

Since we are given an elementary reaction, we can construct a rate law directly from the reaction.

rate = k[A]²[B]

Since we are given the rate, [A] and [B], we simply need to plug these numbers into our new rate law and isolate k.

.3 mol L^-1 s^-1 = k [.02 mol L^-1]² [.1 mol L^-1]

k = 7500 L² mol^-2 s^-1

^{This is a third order reaction: second order in A and first order in B.}

9.10

We are given some data and told to find the reaction order. There are three reaction orders that are commonly seen in this class of problems: zeroth, first and second. Each order of kinetics can be expressed linearly.

Zeroth: \( [A] = [A]_{0} − kt \rightarrow [A] \) varies with t.

First: \( \ln {[A]} = \ln {[A]_0} − kt \rightarrow \ln {[A]} \) varies with t.

Second: \( \frac{1}{[A]} = \frac{1}{[A]_0} +kt \rightarrow \frac{1}{[A]} \) varies with t.

The easiest way to solve this class of problems is to see if the data linearly fits any of the above relationships. Through process of elimination, we find that the data linearly fits second order kinetics:

Therefore, this reaction is second order in A.

k can be found from the equation of the line, where \( y = \frac{1}{[A]} \), \( x = t \), \( m = k \) and \( b = \frac{1}{[A_0]} \).

k, then is the slope of the above line. In this case, k = 20 L mol^-1 s^-1.

9.27

We are given two temperatures and two time periods in which a reaction happens.

Trick: realizing that a time period equates to reaction rate, which is then directly proportional to the rate constant.

\( \dfrac{k_1}{k_2} \) would then be \( \dfrac{10}{20} \) which equals \( \dfrac{1}{2} \).

This can be plugged into the two-point Arrhenius equation, which features all of the variables we have.

\( \ln \dfrac{k_{1}}{k_{2}} = -\dfrac{E_{a}}{k_{B}} \left (\dfrac{1}{T_1} - \dfrac {1}{T_2} \right ) \) \( \rightarrow \) \( \ln \dfrac{1}{2} = -\dfrac{E_{a}}{k_{B}} \left (\dfrac{1}{298} - \dfrac {1}{308} \right ) \) \( \rightarrow \) \(\ E_a = 52894 J \)

10.2

The approach taken in question 9.10 can be used here as well. Through process of elimination, we find that the dissociation of [ES] is first order.

As before, we can find k from the slope of the line. In this case k = 0.1 L mol ^-1 s^-1.

The final part of the problem asks at which concentration of [ES] is the steady-state approximation appropriate.

Usually, enzyme problems of this sort will have three or more equilibrium constants. However, since this problem only features two, it will be simpler to tackle.

The steady-state approximation posits that the rate of formation of the intermediate (ES) equals the rate of dissociation of the intermediate. This is not true for the entirety of the reaction, but it proves a useful approximation when appropriate.

We were given the rate of formation of ES as 5 mol L^-1 s^-1. Therefore, we must find when the concentration of ES results in a rate of 5 mol L^-1 s^-1.

First we must construct a rate law. Since we've already found that the reaction is first order, this will be straight forward.

rate = k[ES]

Now, it is simply a matter of plugging in the numbers we already have.

5 mol L^-1 s^-1 = (.1 L mol ^-1 s^-1) [ES]

[ES] = 50 mol L^-1

11.17

Heat given off by radiation = n \( \cdot \) h \( \cdot \) c

Where n = number of photons, h = planck's constant, and c = speed of light

Kinetic energy of a 1 kg cart moving at 5 m/s:

\(E = \frac{1}{2} m v^{2} \rightarrow E = \frac{1}{2} (1 kg)(5 m/s)^{2} \)

\(E = 12.5 J \)

Now, set the kinetic energy we've found as the heat given off by radiation and isolate n:

\[ 12.5 J = n \cdot 6.626 \times 10^{-34} m^{2} kg s^{-1} \cdot 3 \times 10^{8} m s^{-1} \] \[n = 6.29 \times 10^{25} \]

12.9

These are orbital drawings of each of the given scenarios. Keep in mind: these images are not saying that the electron is always in the positions pictured. These images are simply displaying the most probable location of the electron among the two orbitals.

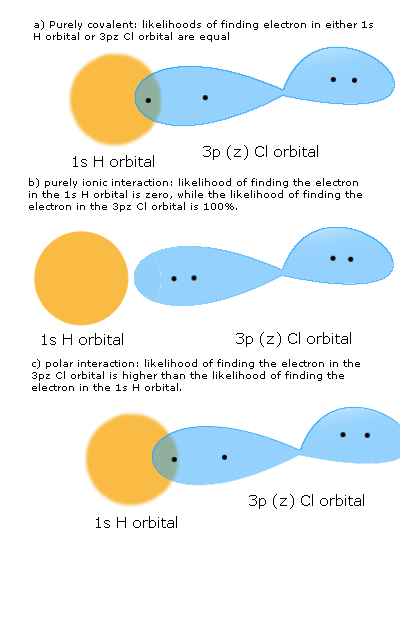
Here is the covalent wave function:

\[ \psi_{covalent} = \psi_H(e_H)\psi_Cl(e_{Cl}) + \psi_H(e_{Cl})\psi_Cl(e_H) \]

Here is the ionic wave function:

\[ \psi_{ionic} = \psi_H(e_H)\psi_H(e_H) + \psi_Cl(e_{Cl})\psi_Cl(e_{Cl}) \]

The polar wave function will look similar to the covalent wave function, as the covalent wave function accounts for the sharing of electrons among orbitals. However, the ultimate values will be different (i.e. the \( \psi_H(e_H) \) and the \( \psi_H(e_{Cl}) \) portions of the wave function will be less heavily weighted than the \(\psi_Cl(e_H) \) and the \( \psi_Cl(e_{Cl}) \) portions of the wave function.)

13.12

For this problem, we'll have to use the Van der Waal's radius of Br.

According to the linked page, the "van der Waals radius is defined as half of the internuclear separation of two non-bonded atoms of the same element on their closest possible approach and is denoted r_v." The van der Waal's radius of bromine shown on the page is 195 pm.

Since this solid is only composed of Br, we simply need to plug in the van der Waal's radius of Br from the table into the formula for the volume of a sphere.

\[ V = \frac{4}{3} \pi r^{3} \rightarrow V = \frac{4}{3} \pi (195 \times 10^{-12} m)^{3}) \rightarrow V = 3.106 \times 10^{-29} m^{3} \]

This is the volume for one bromine atom. In this case, we have 3 moles of bromine. So, we must multiply the above volume by three times Avogadro's number to get \( 5.611 \times 10^{-5} m^{3}\). This is the volume that 3 moles of bromine occupies.

For the bromine atoms to occupy 50% of the volume of the container, the volume of the container must be \( 1.12 \times 10^{-4} m^{3}\).

You now have all of the parameters required (aside from pressure, which you will solve for momentarily) to use the ideal gas law.

\[ P = \frac{nRT}{V} \rightarrow P = \frac{3 \cdot .08206 \cdot 298}{1.12 \times 10^{-4}} \] \[ P = 655015 \hspace{1 pc} atm \]

That's a lot of pressure!

14.15

For this problem, our ultimate goal is to find the energy associated with a \( J = 4 \rightarrow 5 \) energy transition. The formula associated with this is:

\[ \Delta E_{4 \rightarrow 5} = 2BhJ' \]

To use this formula, we must first find B, which has the following formula:

\[ B = \frac{h}{8 \pi^{2} I} \]

And to use the above formula, we must first find I, which has the following formula:

\[ I = \mu r^{2} \]

Luckily, we found \( \mu \) and \( r^{2} \).

\[ I = 1.5 \times 10^{-26} kg \cdot (3 \times 10^{-10})^{2} m = 4.5 \times 10^{-46}\]

So \( B = \frac{6.626 \times 10^{-34}}{8 \cdot \pi^{2} \cdot 4.5 \times 10^{-46}} = 1.86 \times 10^{10} \)

So, \( \Delta E_{4 \rightarrow 5} = 2 \cdot 1.86 \times 10^{10} \cdot 6.626 \times 10^{-34} \cdot 5 \)