Extra Credit 28

Q19.10A

\(\ce{[Zn^{2+}]}\)=1.2M

What \(\ce{[Cu^{2+}]}\) will allow a forward spontaneous reaction?

Net Reaction: \(\mathrm{Zn_{(s)}+Cu^{2+}\rightarrow Cu_{(s)}+Zn^{2+}}\)

S19.10A

Positive \(\ce{E_{cell}}\) means that your reaction is spontaneous so use the Nernst equation setting \(\ce{E_{cell}=0.000V}\) (because zero is the smallest possible positive number) \(\ce{[Zn^{2+}]}\)= 1.0 M

-Finding \(\ce{[Cu^{2+}]}\) at smallest possible positive \(\ce{E_{cell}}\) means that you're finding the minimum \(\ce{[Cu^{2+}]}\) needed to allow a forward spontaneous reaction

Nernst equation: \(\mathrm{E_{cell}= E^{\circ}_{cell} -\frac{0.05922}{n}log(Q)}\)

-n=number of electrons transferred in the balanced redox reaction

Reduction Half-Reaction:\(\mathrm{Cu^{2+}_{(aq)}+2e^{-}\rightarrow Cu_{(s)}}\)

Oxidation Half-Reaction:\(\mathrm{Zn_{(s)}\rightarrow Zn^{2+}+2e^{-}}\)

The number of electrons in the balanced reduction half-reaction need to be the same as those in the oxidation half-reaction in order to combine the two equations and get the overall balanced equation. When the two half-reactions are combined the electrons should cancel out. If the two half-reactions don't have an equal amount of electrons then one or both of the half-reactions would need to be multiplied by a stoichiometric coefficient to make them equal. In this case the number of electrons is already equal so no further balancing is required.

n=2

-\(\ce{E^{\circ}_{cell}}\) is given = 1.100V

-\(\ce{E_{cell}}\)=0.00V (smallest positive number possible)

-\(\mathrm{Q=\frac{[cation in products]}{[cation in reactants ]}=\frac{[Zn^{2+}]}{[Cu^{2+}]}, [Zn^{2+}]}\) is given=1.2 M

Next, plug in these values in the Nernst equation in order to solve for \(\ce{[Cu^{2+}]}\).

\(\mathrm{E_{cell} = E^{\circ}_{cell}- \frac{0.0592}{2}log\frac{[Zn^{2+}]}{[Cu^{2+}]}}\)

\(\mathrm{0.00V = 1.100V - \frac{.0592}{2}log\frac{1.2M}{[Cu^{2+}]}}\)

Now, subtract 1.100 from both sides and multiply both sides by -0.0296 (which is equal to .0592/2).

\(\mathrm{\frac{0.00-1.100}{-0.0296} = log\frac{1.2 M}{[Cu^{2+}]}}\)

\(\mathrm{37.2 = log\frac{1.2 M}{[Cu^{2+}]}}\)

Make both sides of the equation an exponent of e in order to cancel out the logarithim and then utilize simple algebra to solve for \(\ce{[Cu^{2+}]}\).

\(\mathrm{10^{37.2}=\frac{1.2M}{[Cu^{2+}]}}\)

\(\mathrm{10^{37.2}[Cu^{2+}]=1.2M}\)

\(\ce{[Cu^{2+}]=8.4 x 10^{-17}}\)

Q19.75A

In the two galvanic cells created the following variations occur:

1. \(\mathrm{L^{2+}_{(aq)}+LO^{2+}_{aq}+2H^{+}_{aq}\rightarrow 2L^{3+}_{aq}+H_{2}O_{l}E^{\circ}=0.616V}\)

2. \(\mathrm{L^{3+}_{aq}+Ag^{+}_{aq}+H_{2}O\rightarrow LO^{2+}_{aq}+2H^{+}+Ag_{s}E^{\circ}=0.439V}\)

Use other values as well as the data presented here to determine \(\ce{E^{\circ}}\) for the half reaction:

\(\mathrm{L^{3+} +e^{-}\rightarrow L^{2+}}\)

S19.75A

With the second equation, find it's two half reactions. One of the half reactions would be one of the two that are listed in the question and the other should be the opposite of a half-reaction for the first equation. In this case, since Ag is present in the second equation and not the first, one of the half reactions is \(\mathrm{Ag^{+}+e^{-}\rightarrow Ag_{(s)}}\) and the second half reaction is the remainder of the balanced equation. You can refer to the original balanced equation to see that \(\ce{Ag^{+}}\) is gaining electrons so the half-reaction \(\mathrm{Ag^{+}+e^{-}\rightarrow Ag_{(s)}}\) is the reduction reaction. As a result, the other half-reaction must be an oxidation reaction.

Ox: \(\mathrm{L^{3+}+H_{2}O\rightarrow LO^{2+}+2H^{+}+e^{-} E^{\circ}=-E^{\circ}_{a}}\)
Red: \(\mathrm{Ag^{+}+e^{-}\rightarrow Ag_{(s)}E^{\circ}=0.800V}\)
------------------------------------------------------------------------------------
Overall: \(\mathrm{E^{\circ}_{cell}=-E^{\circ}_{a}+E^{\circ} _{red}}\)

The reduction cell potential of the reduction equation can be determined by looking at a standard reduction potential table. You're trying to solve for the standard reduction potential of the oxidation equation in order to use that value for the standard reduction potential of the half-reaction in the first equation. As a result, use the given \(\ce{E^{\circ}_{cell}}\) value for the second balanced equation and the standard reduction potential value for the half-reaction \(\mathrm{Ag^{+}+e^{-}\rightarrow Ag_{(s)}}\) to solve for the standard reduction potential of the other half-reaction. We can assign a variable to the standard reduction we're solving for: \(\ce{E_{a}^{^{\circ}}}\). Since an oxidation reaction is the reverse of a reduction reaction, the standard cell potential of the oxidation reaction is negative.

The two half reactions combined give you the complete balanced reaction, this same logic applies to their standard reduction potentials.

\(\ce{0.439V=-E_{a}^{^{\circ}}+0.800V}\)

Use algebra to solve for \(\ce{E_{a}^{^{\circ}}}\)

\(\ce{E_{a}^{^{\circ}}=0.361V}\)

Ox: \(\mathrm{L^{2+}\rightarrow L^{3+}+e^{-}}\) \(\ce{E^{\circ}=-E_{b}^{\circ}}\)
Red: \(\mathrm{LO^{2+}+2H^{+}+e^{-}\rightarrow L^{3+}+H_{2}O}\) \(\ce{E^{\circ}=0.361 V}\)
------------------------------------------------------------------------------------
Overall: \(\mathrm{E^{\circ}_{cell}=-E^{\circ}+E_{red}^{\circ}}\)

The two half reactions combined give you the complete balanced reaction, this same logic applies to their standard reduction potentials.

\(\mathrm{E_{cell}^{\circ}= -E_{b}^{\circ}+0.361V}\)

For the half reaction \(\mathrm{LO^{2+}+2H^{+}+e^{-}\rightarrow L^{3+}+H_{2}O}\), the standard reduction potential that was solved for above,0.361 V, can be used considering that the half-reactions \(\mathrm{L^{3+}+H_{2}O\rightarrow LO^{2+}+2H^{+}+e^{-}}\) and \(\mathrm{LO^{2+}+2H^{+}+e^{-}\rightarrow L^{3+}+H_{2}O}\) are simply opposites of each other. But, since the half-reaction \(\mathrm{LO^{2+}+2H^{+}+e^{-}\rightarrow L^{3+}+H_{2}O}\) is a reduction reaction, it's standard reduction potential would be positive. Now we're solving for the standard reduction potential of the oxidation half reaction of\(\mathrm{L^{2+}\rightarrow L^{3+}+e^{-}}\), assigned with the variable \(\ce{-E_{b}^{\circ}}\). Once again, the value is negative because it is for an oxidation equation. The value 0.616 V was given as the value of \(\ce{E_{cell}^{\circ}}\) for the balanced half reaction.

\(\mathrm{0.616V=-E_{b}^{\circ}+0.361V}\)

Use algebra to solve for \(\ce{E_{b}^{\circ}}\).

\(\ce{E_{b}^{\circ}=-0.225V}\)

Q21.5E

1. The complex ion \(\ce{[Co(CN)_{4}]^{2-}}\) is paramagnetic with three unpaired electrons. What are some possible structures using the ideas the crystal field theory.
2. Is \(\ce{[Cu(NH_{3})_{4}]^{2+}}\) paramagnetic or diamagnetic? Knowing this complex has magnetic properties. Can you determine the structure of \(\ce{[Cu(NH_{3})_{4}]^{2+}}\) is tetrahedral or square-planar? why?

S21.5E

1. In \(\ce{[Co(CN)_{4}]^{2-}}\) Co has a +2 charge. This is determined by knowing that the charge of CN is -1 and that the sum of the charges in the complex needs to be -2. With this we can solve for the charge of Co with the equation: x + (-4) = -2 with x being the charge of Co.

Next, determine the electron configuration of \(\ce{Co^{2+}}\). By looking at the periodic table we can see that the electron configuration of Co is \(\mathrm{[Ar]4s^{2}3d^{7} }\). Since Co loses two electrons to be \(\ce{Co^{2+}}\), the two electrons from the 4s shell are lost.Therefore, we can conclude the electron configuration of \(\ce{Co^{2+}}\) is \(\mathrm{[Ar]3d^{7}}\).

So it has 7 d-orbital electron since it is paramagnetic we know it has to be Octahedral since two lower subshells are filled with 4 electron and the top three subshells are filled with one unpaired electrons each compared to the Octahedral structure with 6 electrons in the lower subshells and one unpaired electron in the high subshell.

2. In \(\ce{[Cu(NH_{3})_{4}]^{2+}}\) Cu has a +2 charge. This is determined by knowing that the charge of \(\ce{NH_{3}}\) is 0 and that the sum of the charges in the complex needs to be +2. With this we can solve for the charge of Cu with the equation x + 0 = 2 with x being the charge of Cu.

Next, determine the electron configuration of \(\ce{Cu^{2+}}\). By looking at the periodic table we can see that the elecron configuration of Cu is \(\mathrm{[Ar]4s^{1}3d{10}}\). Since Cu loses two electrons to be \(\ce{Cu^{2+}}\), one electron from the 4s shell and another from the 3d shell are lost.Therefore we can conclude the electron configuration of \(\ce{Cu^{2+}}\) is \(\mathrm{[Ar]3d^{9}}\).

As a result, \(\ce{Cu^{2+}}\) has 9 d-orbital electrons and we know it has magnetic property it means that it is paramagnetic. Looking at the figure we can see that the square-planar structure has a magnetic structure with one unpaired electron on its highest subshell compared to the tetrahedral structure with one of the three subshells having an unpaired electron.

Q24.13E

The following rates of reactions were obtained in three experiments with the reaction \(\mathrm{2NO_{(g)}+Cl_{2}\rightarrow 2NOCl_{(g)}}\)

What is the order of the reaction with respect of A and B? Write out respective rate laws for A and B

S24.13E

m and n are the respective orders according to [NO] and \(\ce{[Cl_{2}]}\):

\(\mathrm{R1=1.45x10^{-5}=[0.362]^{m}[0.730]^{n}}\)

\(\mathrm{R2=2.90×10−5=[0.362]^{m}[1.46]^{n}}\)

\(\mathrm{R3=5.80×10−5=[0.724]^{m}[0.730]^{n}}\)

Now utilize the rate laws and solve:

First, solve for the order with respect to \(\ce{Cl_{2}}\):

Divide R2 by R1 ([NO] stays constant while \(\ce{[Cl_{2}]}\) changes)

\(\mathrm{\frac{R2}{R1}=\frac{2.9x10^{-5}}{1.45x10^{-5}}=\frac{[0.362]^{m}[1.46]^{n}}{[0.362]^{m}[0.730]^{n}}}\)

The \(\ce{[0.362]^{m}}\) in the numerator cancels out with the one in the denominator to equal one. When you divide the two rates by each other you get 2; when you divide the two concentrations by each other you also get two.

\(\mathrm{\frac{R2}{R1}=2=2^{n}}\)

Now find a value for n that would allow the equation \(\ce{2=2^{n}}\) to hold true.

n=1

Since n is the order of \(\ce{[Cl_{2}]}\) the reaction is first order with respect to \(\ce{Cl_{2}}\).

Second, find the order with respect to NO.

Divide R3 by R1 (\(\ce{[Cl_{2}]}\) is constant while [NO] changes)

\(\mathrm{\frac{R3}{R1}=\frac{5.8x10^{-5}}{1.45x10^{-5}}=\frac{[0.724]^{m}[0.730]^{n}}{[0.362]^{m}[0.730]^{n}}}\)

The \(\ce{[0.730]^{n}}\) in the numerator cancels out with the one in the denominator to equal one. when you divide the two rates by each other you get 4; when you divide the two concentrations by each other you get 2.

\(\mathrm{\frac{R3}{R1}=4=2^{m}}\)

Now find a value for m that would allow the equation \(\ce{4=2^{n}}\) to hold true.

m=2

Since m is the order of [NO] the reaction is second order with respect to [NO]

In rate laws, the orders are exponents of their respective concentrations.

\(\mathrm{Rate Law=k[NO]^{2}[Cl_{2}]}\)

Using the rate law we can solve for k, the rate constant

You can the values from any set of experimental data to plug into the rate law equation.

Lets use exp. 2, for example.

\(\mathrm{2.9x10^{-5}Ms^{-1}=k[NO]^{2}[Cl_{2}]=k[0.362]^{2}[1.46]}\)

Use algebra to solve for k.

\(\mathrm{k=1.52x10^{-4}M^{-2}s^{-1}[NO]^{2}[Cl_{2}] = 1.52 x10^{-4}}\)

Q24.63A

What reaction conditions are necessary to produce a straight-line graph of reaction rate vs. enzyme concentration?

S24.63A

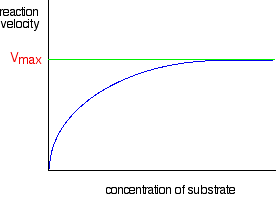
In biology and biochemistry, the reactant in an enzyme reaction is known as the "substrate".

This graph is the shape it is because:

1. For very low concentrations, the graph is a straight line. This means that at very low concentrations, the rate is proportional to the substrate concentrations, producing a straight-line graph. This can be seen in the bottom left corner portion of the graph above.
2. As the concentration increases, the increasing concentration has less and less effect and eventually the rate reaches a maximum; increasing the concentration anymore won't make a difference to the rate reaction after this point. This can be seen in the graph above when after a certain point the graph doesn't increase anymore and begins to plateau.

Q25.29D

\(\mathrm{_{83}^{209}\textrm{Bi}/_{91}^{231}\textrm{Pa}}\) is in a meteorite approximately \(\ce{2.6 x 10^{9}}\) years old. The half-life of \(\mathrm{_{91}^{231}\textrm{Pa}}\) is \(\ce{1.21 x 10^{10}}\) years. What should the mass ratio be of \(\mathrm{_{83}^{209}\textrm{Bi}/_{91}^{231}\textrm{Pa}}\)?

S25.29D

You can utilize the equation \(\ce{\lambda =\frac{0.693}{t_{1/2}}}\) and the given value \(\ce{t_{1/2}=1.21 x 10^{10}}\) to solve for lambda.

Plug in the half-life value into the equation.

\(\mathrm{\lambda =\frac{0.693}{1.21x10^{10}years}}\)

\(\mathrm{\lambda=5.73x10^{-11}}\) years

Next use the equation \(\mathrm{ln(\frac{N_{t}}{N_{o}}) = -kt}\) and solve for \(\mathrm{\frac{N_{t}}{N_{o}}}\) to find the ratio of moles of \(\mathrm{_{91}^{231}\textrm{Pa}}\) over initial moles of \(\mathrm{_{91}^{231}\textrm{Pa}}\).

Plug the value of lambda that was previously solved for in for k and then plug in the meteorite's age for t.The meteorite's age was given in the original question as \(\ce{2.6 x 10^{9}}\) years old.

\(\mathrm{ln(\frac{N_{t}}{N_{o}})=(-5.7x10^{-11})(2.6x10^{9})}\)

\(\mathrm{ln(\frac{N_{t}}{N_{o}})=-0.14898}\)

Make both sides of the equation an exponent of e in order to cancel out the natural log on the left side of the equation.

\(\mathrm{\frac{N_{t}}{N_{o}}=0.861586}\)

This value shows that for every mol of \(\mathrm{_{91}^{231}\textrm{Pa}}\) present initially, there is \(\mathrm{0.861 mol_{91}^{231}\textrm{Pa}}\) and \(\mathrm{0.139 mol _{83}^{209}\textrm{Bi}}\).

We can use stoichiometric ratios of the atomic masses of each element to convert the ratio from moles to grams.

\(\mathrm{(\frac{0.159 mol _{83}^{209}\textrm{Bi}}{0.861 mol _{91}^{231}\textrm{Pa}})(\frac{209g}{1 mol _{83}^{209}\textrm{Bi} })(\frac{1 mol_{91}^{231}\textrm{Pa}}{231g} )=\frac{0.167g_{83}^{209}\textrm{Bi}}{1g_{91}^{231}\textrm{Pa}}}\)

Q21.1.7

Because radon is a noble gas, it is inert and generally unreactive. Despite this, exposure to even low concentrations of radon in air is quite dangerous. Describe the physical consequences of exposure to radon gas. Why are people who smoke more susceptible to these effects?

S21.1.7

Radon is one of the products of radioactive decay in Uranium, along with alpha particles. Radon, as a radionuclide, is also unstable and undergoes a series of radioactive decays until it eventually reaches the stable product lead. Through this radioactive decay, multiple alpha particles are emitted into the air which we inhale. Depending on the concentration of radon that one is exposed to, the inhalation of alpha-particles damage the cells that line the airways of your lungs and can lead to lung cancer.

Because of the common knowledge that smoking can cause cancer, it is obvious that the risk of lung cancer is much higher when there is a combination of radon exposure and smoking. As a matter of fact, those that smoke and are exposed to radon are ten times more likely to get lung cancer than those that don't smoke and are still exposed to radon.

Q24.6.4

For an octahedral complex of a metal ion with a d6 configuration, what factors favor a high-spin configuration versus a low-spin configuration?

S24.6.4

Typically, the nature of the ligands in the complex determines the spin configuration.

If the metal ion is bonded with weak field ligands, then the coordination complex has a high-spin configuration. This is due to the fact that weak field ligands cause the transition metal to have a low crystal field splitting. When the crystal field splitting energy is lower than the pairing energy then this means that it is more energetically favorable for electrons to half fill the \(\ce{e_{g}}\) orbitals rather than completely fill the \(\ce{t_{2g}}\) orbitals. As a result, the complex has a high-spin configuration.

If the metal ion is bonded with strong field ligands, then the coordination complex has a low-spin configuration. This is due to the fact that strong field ligands cause the transition metal to have a high crystal field splitting. When the crystal field splitting energy is higher than the pairing energy then this means that it is more energetically favorable to completely fill the already half-filled \(\ce{t_{2g}}\) orbitals than half-fill the \(\ce{e_{g}}\) orbitals. As a result, the complex has a low spin-configuration.