Extra Credit 45

Q17.6.4

Suppose you have three different metals, A, B, and C. When metals A and B come into contact, B corrodes and A does not corrode. When metals A and C come into contact, A corrodes and C does not corrode. Based on this information, which metal corrodes and which metal does not corrode when B and C come into contact?

S17.6.4

Given: Metals A,B, and C

Asked for: Which metal corrodes when in contact B or C?

Strategy:

Corrosion is the degradation of a material due to reaction with the environment more specifically, a redox reaction. Metals, which have the smaller standard reduction potential, are more vulnerable to corrode as they act as the anode, donating electrons, and becoming an ion. Since

\[E^{°}_B < E^{°}_A\] and \[E^{°}_A < E^{°}_C\]

then it goes that

\[E^{°}_B < E^{°}_A< E^{°}_C\]

This concludes that metal B will corrode (Edit: acting as the sacrificial anode) and protect C when they come into contact.

Q12.3.8

The rate constant for the radioactive decay of ¹⁴C is 1.21 × 10⁻⁴ year⁻¹. The products of the decay are nitrogen atoms and electrons (beta particles):

\[{^{14}_{6}C⟶^{14}_{7}N + e^{-}}\]

\[rate=k[^{14}_{6}C]\]

What is the instantaneous rate of production of N atoms in a sample with a carbon-14 content of 6.5 × 10⁻⁹ M?

S12.3.8

Given: Rate Constant

Asked for: Instantaneous rate of reaction

Strategy:

Notice that this is a first order reaction, therefore any change in concentration will affect the overall rate of the reaction.

By knowing the concentration and the rate constant, we can calculate the expected speed of this reaction at that exact concentration.

Instantaneous rate of reaction is the rate of reaction at any instant of time during the progress of reaction.

First, we know that the rate law for this equation is as follows:

\[rate=k[^{14}_{6}C]\]

Where k (rate constant) = 1.21 × 10⁻⁴ year⁻¹ and the concentration of carbon-14 is 6.5 × 10⁻⁹ M.

Substitute these values into the rate law equation.

\[rate=k[^{14}_{6}C]\]

\[=1.21 × 10^{-14} year^{-1}×6.5 × 10^{-9}M\]

\[=7.865×10^{-13}M year^{-1}\]

\[rate=-\frac{Δ[^{14}_{6}C]}{Δt}=+\frac{Δ[^{14}_{6}C]}{Δt}=+\frac{Δ[e^{-}]}{Δt}\]

Thus the instantaneous rate of production of N-atoms is 7.865×10^-13M year^-1

^{Edit: The original question asked was messed up}

Q12.5.17

Use the PhET Reactions & Rates interactive simulation to simulate a system. On the “Single collision” tab of the simulation applet, enable the “Energy view” by clicking the “+” icon. Select the first \(A+BC\rightarrow AB+C\) reaction (A is yellow, B is purple, and C is navy blue). Using the “angled shot” option, try launching the A atom with varying angles, but with more Total energy than the transition state. What happens when the A atom hits the BC molecule from different directions? Why?

S12.5.17

Given: A Atom , BC Molecule , Simulation software

Asked for: Find different behaviors of the atoms interactions and why it occurs.

Strategy:

This question asks to figure out what happens in the scenario when the A atom hits the BC molecule from different directions/angles. It also asks us to explain why this occurs. The two postulates of the Collision Theory that are relevant to this question is

1. The reacting species must collide in an orientation that allows contact between the atoms that will become bonded together in the product.
2. The collision must occur with adequate energy to permit mutual penetration of the reacting species’ valence shells so that the electrons can rearrange and form new bonds (and new chemical species).

Below is a standard energy diagram

The transition state is the peak of the graph. For a reaction to occur, it has to have adequate energy to overcome the activation energy or rather the minimum amount of energy needed (E_a).

When atom A is hit straight on with enough total energy to overcome the potential energy, you can see that a reaction occurs between molecule A and molecule BC. There is enough energy here for a reaction to occur , and it is also hit in the correct orientation.

Figure 1.1: A straight on molecule collision

However, it is clear that if the molecule is not hit in the proper orientation then no reaction will occur. Another case where no reaction will occur is if there is not enough total energy at collision.

Figure 1.2: An angled collision

So in conclusion, the A atom has enough energy to react with BC; however, the different angles at which it bounces off of BC without reacting indicate that the orientation of the molecule is an important part of the reaction kinetics and determines whether a reaction will occur. Also, the reaction does not proceed if there is not enough energy for the two compounds to react despite the proper spatial orientations.

Q21.4.12

Write a nuclear reaction for each step in the formation of \({^{208}_{82}Pb}\) from \({^{228}_{90}Th}\), which proceeds by a series of decay reactions involving the step-wise emission of α, α, α, α, β, β, α particles, in that order.

S21.4.12

Given: Atomic Number, Mass number

Asked for: Series of decay reactions

Strategy:

α Particles: These are basically the divalent cation of helium or nucleus of helium with two protons and four neutrons which is emitted from the nucleus. It is symbolized by \[^4_2He\]

β Particles: These are called beta particles and can either be an electron or a positron (anti-electron). These are the electrons having high energy which are released during the radioactive decay of the unstable nucleus.Depending on whether it is an electron or a positron dictates what change will happen in the nucleus. If an electron is emitted, it is from a neutron transforming into a proton. If it is a positron emitted, then a proton has transformed into a neutron. For electron emission, it is symbolized by \[^0_1e\]. For positron emission, it is symbolized by \[^0_{-1}e\].

For every α emitted. Atomic number is subtracted by 2 and the Mass number is reduced by 4. For example the first step:

\[{^{228}_{90}Th}⟶^{224}_{88}Ra+α\]

For every β particle emission , the mass number stays the same and the atomic number is increased by 1. For example:

\[{^{212}_{82}Pb}⟶^{212}_{83}Bi + β\]

So.. The step-wise emission of α, α, α, α, β, β, α particles is:

\[^{228}_{90}Th⟶^{224}_{88}Ra+α ;^{224}_{88}Ra⟶^{220}_{86}Rn+α \] \[;^{220}_{86}Rn⟶^{216}_{84}Po+α ;^{216}_{84}Po⟶^{212}_{82}Pb+α \]\[;^{212}_{82}Pb⟶^{212}_{83}Bi+β ;^{212}_{83}Bi⟶^{212}_{84}Po+β \]\[;^{212}_{84}Po⟶^{208}_{82}Pb+α\]

Q20.2.16

Classify each reaction as an acid–base reaction, a precipitation reaction, or a redox reaction, or state if there is no reaction; then complete and balance the chemical equation:

1. Zn(s) + HCl(aq) →
2. HNO₃(aq) + AlCl₃(aq) →
3. K₂CrO₄(aq) + Ba(NO₃)₂(aq) →
4. Zn(s) + Ni²⁺(aq) → Zn²⁺(aq) + Ni(s)

S20.2.16

Given: Reactions

Asked for: Complete and Identify the type of reaction

Strategy:

1. Zn(s) + 2HCl(aq) → ZnCl₂(s)+H₂(g)

Redox Reaction(single replacement). A redox reaction is a type of chemical reaction that involves transfer of electrons between two species. The oxidation number of a molecule , atom or ion changes by gaining or losing an electron. In this reaction we can see observe that Zn is going from +0 to +1(Mistake: Zn is going to +2 oxidation state)(oxidation) , so it is losing 1(Mistake: losing 2 electrons) electron.The two hydrogen ions are going from +1 to +0(reduction) , so it is gaining 1 electron to become a neutral molecule.

Oxidation is the loss of electrons , so Zn is getting oxidized(also known as the reducing agent). Where hydrogen is the oxidizing agent. Add 2 in front of HCl in order to balance the following chemical equation.

2. HNO₃(aq) + AlCl₃ (aq)→ 3HCl(aq) + Al(NO₃)₃(s)

Precipitation Reaction. (Double Replacement) A precipitation reaction occurs when cations and anions in aqueous solution combine to form an insoluble ionic solid called a precipitate. In this example the Al(NO₃)₃ is the precipitate (will usually be a solid), so we know it is a precipitate reaction. It is important to note that this is also a double replacement reaction where the two ionic reactants dissociated in water and bonded with their respective anion or cation from the other reactant. (Refer to image) A 3 is required in front of HCl in order to balance the chemical equation.

Figure 1.3: a double replacement reaction

3. K₂CrO₄(aq) + Ba(NO₃)₂ (aq) → BaCrO₄(s) + 2KNO₃(aq)

Precipitation Reaction.(Double Replacement) A precipitation reaction occurs when cations and anions in aqueous solution combine to form an insoluble ionic solid called a precipitate. In this example the BaCrO₄ is the precipitate, so we know it is a precipitate reaction. It is important to note that this is also a double replacement reaction where the two ionic reactants dissociated and bonded with their respective anion or cation from the other reactant. A 2 is required in front of KNO₃ in order to balance the chemical equation.

4. Zn(s) + Ni²⁺(aq) → Zn²⁺(aq) + Ni(s)

Redox Reaction. A redox reaction is a type of chemical reaction that involves transfer of electrons between two species. The oxidation number of a molecule , atom or ion changes due to gaining or losing an electron. In this reaction we observe that Zn is going from +0 to +2 , so it is losing 2 electrons (becomes more positive). Ni is going from +2 to +0 , so it is gaining 2 electrons (becomes more negative).

Oxidation is the loss of electrons , so Zn is getting oxidized(also known as the reducing agent). Ni is the oxidizing agent because it is reduced.

The half cells:

Zn²⁺+ 2e^- → Zn

Ni²⁺ + 2e^- → Ni

Also note that the reduction potential of Zinc is -0.76 V while Nickel has a reduction potential of -0.25V. Because nickel is more positive, you know that it is reduced. Thus Zinc is the element that gets oxidized.

Q20.5.11

The chemical equation for the combustion of butane is as follows:

\[\mathrm{C_4H_{10}(g)+\frac{13}{2}O_2(g)\rightarrow4CO_2(g)+5H_2O(g)}\]

This reaction has ΔH° = −2877 kJ/mol. Calculate E°_cell and then determine ΔG°. Is this a spontaneous process? What is the change in entropy that accompanies this process at 298 K?

S20.5.11

Given: Enthalpy, Chemical equation , temperature

Asked for: Cell potential and Change in Free energy

Strategy:

Step 1:

(Figure 1.8) - Gibbs Equations

Since there is a circle next to delta H, E cell, etc., it means "standard," in that you have to find these values at standard conditions.

K (which is used to find ΔG° with the equation ΔG°=-RT*ln K_eq) is 1 at standard conditions (since gas pressures = 1 bar and K= concentrations/gas pressures of products/ concentrations/gas pressures of reactants).

Plugging in K=1 into the equation ΔG°=-RT*ln K_eq, we find that ΔG°=0. This means that the reaction is at equilibrium and is neither spontaneous nor non-spontaneous.

To calculate E°_cell, use the equation: ΔG°=-nFE°_cell, where n is the number of electrons and F is Faraday's constant. Since ΔG°=0, E°_cell=0 as n is not zero due to redox and F is a positive constant..

To find the change in entropy, or ΔS°, use the equation: ΔG°= ΔH° - TΔS°, where T is temperature in kelvin.

So, the equation (after plugging in given ΔH°, ΔG°, and T values) would be 0 = −2877 kJ/mol - 298*ΔS°.

Solving for ΔS°, we get that the change in entropy= -9.65 kJ/mol, which is equivalent to about -9650 J/mol .

Q24.6.7

For each complex, predict its structure, whether it is high spin or low spin, and the number of unpaired electrons present.

a. [TiCl₆]³⁻

b. [CoCl₄]²⁻

S24.6.7

Given: Chemical Compound & Overall Charge

Asked for: Structure, spin and number of unpaired electrons

Strategy:

This question asks for the chemical structure , high spin or low spin and the number of unpaired electrons.

a. [TiCl₆]³⁻

Since we know there are 6 electron groups (coordination number of 6) then the molecular structure should be an octahedral. (Refer to Figure 1.4)

(Figure 1.4) - Electron Group Chart

In order to determine the spin of the complex , we can use the spectrochemical scale. (Refer to Figure 1.5). The higher that the ion is on the series ,the lower the spin is. So in this case Cl^- would allow high spin since it is a weak field ligand.

\[\mathrm{I^-<Br^-<Cl<^-SCN^-<F^-<OH^-<ox²^-< ONO^-<H2O<SCN^-<EDTA^(4^-) <NH3<en<NO2^-<CN^-} \]

Where elements and molecules more on the left are weak field ligands and those more on the right are strong field ligands. Weak allow high spin and strong are low spins.

(Figure 1.5) - Spectrochemical Scale

Next determine the electron configuration. By looking at the periodic table , we can determine that the electron configuration of Ti is [Ar]3d² 4s² . So Ti³⁺ should be [Ar]3d¹ due to the 3⁺ charge. Note that s orbital electrons are removed first before any d orbitals can be removed. Since the 3d orbital has only 1 electron,that means it is unpaired. Therefore there is 1 unpaired electron in this complex.

(Figure 1.7) - Crystal Field Splitting Diagram of Ti³⁺

b. [CoCl₄]²⁻

Since we know there are 4 electron groups (Coordination number of 4) then the molecular structure should be an tetrahedral. (Refer to Figure 1.4)

In order to determine the spin of the complex , we can use the spectrochemical scale. (Refer to Figure 1.5). The higher that the ion is on the series ,the lower the spin is. So in this case Cl^- would be high spin since it is one of the lowest on the scale. Cl^- is also classified as a weak field ligand. This is the same as part a.

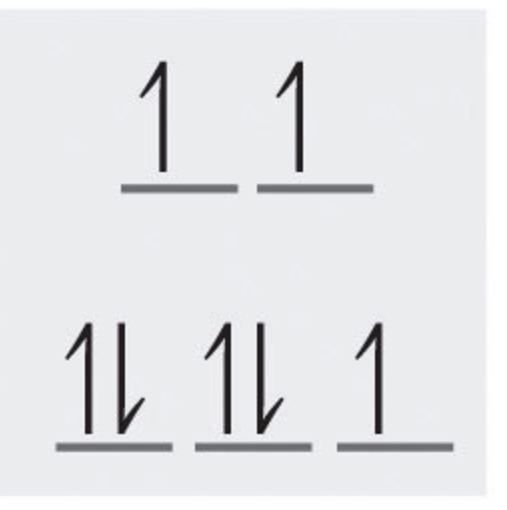
(Figure 1.6) - Crystal Field Splitting Diagram of Co²⁺

Next determine the electron configuration. By looking at the periodic table , we can determine that the electron configuration of Co is [Ar]3d⁷ 4s² . So Co²⁺ should be [Ar]3d⁷ due to the 2⁺ charge. The two s orbital electrons are removed first. Since the 3d orbital has 7 and the total possible is 10, the total number of unpaired electrons is 3.

Edit- Note: When drawing the crystal field splitting diagram, one must take into account whether the complex has a low spin or high spin. For example, when drawing the complex with Co (high spin) you first add one electron to each orbital before filling them entirely. If it were a low spin complex you would fill the bottom orbitals first.