Extra Credit 21 (double)

Q17.2.10

The mass of three different metal electrodes, each from a different galvanic cell, were determined before and after the current generated by the oxidation-reduction reaction in each cell was allowed to flow for a few minutes. The first metal electrode, given the label A, was found to have increased in mass; the second metal electrode, given the label B, did not change in mass; and the third metal electrode, given the label C, was found to have lost mass. Make an educated guess as to which electrodes were active and which were inert electrodes, and which were anode(s) and which were the cathode(s).

S17.2.10

Active electrodes are involved in the reaction where they either gain or lose mass based on the reaction occurring. Inert electrodes do not participate in the reaction itself, but solely serve as a medium for electron flow. The first and third metal electrodes increase and decrease in mass respectively, and therefore must be active electrodes. Because the second electrode stays constant in mass, it is likely for it to be inert. The oxidation reaction occurs at the anode, which means the metal electrode is losing electrons and therefore losing mass, corresponding to electrode C. The reduction reaction occurs at the cathode, which means the metal electrode is gaining electrons and therefore gaining mass, corresponding to electrode A.

Q19.1.19

Predict the products of the following reactions and balance the equations.

1. \(Zn\) is added to a solution of \(Cr_2(SO_4)_3\) in acid.
2. \(FeCl_2\) is added to a solution containing an excess of \(Cr_2O_7^{2-}\) in hydrochloric acid.
3. \(Cr^{2+}\) is added to \(Cr_2O_7^{2-}\) in acid solution.
4. \(Mn\) is heated with \(CrO_3\).
5. \(CrO\) is added to \(2HNO_3\) in water.
6. \(FeCl_3\) is added to an aqueous solution of \(NaOH\).

S19.1.19

In order to write these equations, identify the oxidation states. Knowing the oxidation states will help to determine which elements are going to be oxidized or reduced. We can also determine which elements will be oxidized or reduced by looking at the voltages from a standard reduction potential table. The more positive voltages will be a reduction reaction and the more negative voltage will be for oxidation reaction. Knowing this information, can help us in constructing a balenced equation.

1.\( 2Zn (s) + Cr_2(SO4)_3 (aq) + 2H_3O^+ (aq) → 2Zn^{2+} (aq) + H_2 (g) + 2H_2O (l) + 2Cr^{2+} (aq) + 3SO_4^{2-} (aq)\)

2. \(6FeCl_2 (s) + 14H^+ (aq) + Cr_2O_7^{2-} (aq) → 6Fe^{3+} (aq) + 12Cl^- (aq) + 2Cr^{3+} (aq) + 7H_2O (l)\)

3. \(14H^+ (aq) + 6Cr^{2+} (aq) + Cr_2O_7^{2-} (aq)→ 8Cr^{3+} (aq) + 7H_2O (l)\)

4. \(9Mn (s) + 8CrO_3 (s) → 4Cr_2O_3 (s) + 3Mn_3O_4 (s)\)

5. \(2CrO (s) + 6H^+ (aq) + NO_3^- (aq) → 2Cr^{3+} (aq) + NO_2^- (aq)+ 3H_2O (l)\)

6. \(FeCl_3 (s) + 3NaOH (aq)→ 3NaCl (aq) + Fe(OH)_3 (s)\)

Q19.3.11

Would you expect the \(Mg_3[Cr(CN)_6]_2\) to be diamagnetic or paramagnetic? Explain your reasoning.

S19.3.11

Given the transition metal complex \(Mg_3[Cr(CN)_6]_2\), it is composed of the counter-ion \(Mg\), with a coordination sphere of \([Cr(CN)6]\) that has \(Cr\) as the central metal atom and \(CN\) as the ligand. To determine its magnetism, we focus on the coordination sphere, specifically the oxidation state of the central metal atom, the # of d-electrons of the metal, the geometry of the transition metal complex, and the strength of the ligand(s). Although there is a 2 after the coordination sphere, the charge of the coordination sphere is -3, while the \(Mg\) ion is +2 charge. \(CN\) has a -1 charge, so six of \(CN\) totals to -6, and so “x” oxidation state of \(Cr\) + (-6) = -3, giving \(Cr\) to have a oxidation state of +3. \(Cr^{3+}\) has a total of 3 d-electrons.

Because Cr has six ligands attached, we know that will take on an octahedral structure. Below is an image for an octahedral structure.

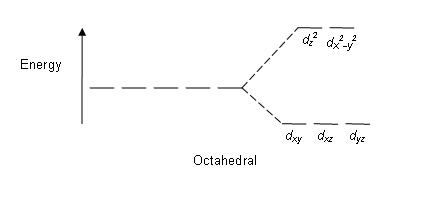
We now look at the strength of the \(CN\) ligand based on the spectrochemical series, which we can find \(CN\) to be a strong-field ligand. Strong-field ligands have higher crystal field splitting energy between the \(e_g\) and \(t_{2g}\) orbitals due to greater overlap and therefore greater repulsion. A low spin structure exhibits greater crystal field splitting energy than pairing energy, so this complex will be low spin. \([Cr(CN)_6]\) has an octahedral geometry, and will be low spin, so the 3 d-electrons will first fill the \(t_{2g}\) orbitals.

By Hund’s Rule, each electron singly fills each orbital before pairing, so there will be 3 unpaired electrons, and \(Mg_3[Cr(CN)_6]_2\) is paramagnetic.

Q12.4.11

The half-life of a reaction of compound A to give compounds D and E is 8.50 min when the initial concentration of A is 0.150 mol/L. How long will it take for the concentration to drop to 0.0300 mol/L if the reaction is (a) first order with respect to A or (b) second order with respect to A?

S12.4.11

First write our reaction and all the given variables

Reaction: \(A \to D + E\)

\(t_{1/2}\)= 8.50 min

\({[A]_0}\) = 0.150 M

The general rate law is as follows:

Rate = \(k[A]^m\), where m being the reaction order with respect to A.

(a) Since the reaction is first order with respect to A, so let m=1

The general rate law is:

Rate = \(k[A]^1 = k[A]\)

For a first order reaction, the half-life is as follows: \(t_{1/2}= {ln(2)\over k}\).

Note: The half-life is independent of initial concentration.

Solve for k, in order to obtain the rate constant.

\(k = {ln(2)\over t_{1/2}}\)

\(k={(ln2)\over 8.50 min} = 0.081547 1{1\over min}\)

To find the time it takes for the concentration to drop to 0.0300 mol/L, we use the following equation for first order reactions:

\(ln[A] = ln[A]_0 -kt\)

Plug in the given values to solve for "t."

\(ln[0.00300 M]= ln[0.150 M] - (0.081547 {1\over min}) t\)

\(t={ ln (0.150 M) - ln (0.00300 M) \over 0.081547 {1\over min}} = 47.97 min\).

The time it takes for the concentration of compound A to drop from 0.150 mol/L to 0.0300 mol/L when the reaction is first order with respect to A is about 47.97 minutes.

(b) Since the reaction is second order with respect to A, we let m=2, so that the general rate law is:

Rate= \(k[A]^2\)

For a second order reaction, the half-life is as follows: \(t_{1/2}={ 1\over k[A]_0}\). Notice that unlike the first order half-life equation, the second order half-life depends on the initial concentration of compound A.

We solve for k, the rate constant:

\(k= {1\over{(t_{1/2})[A]_0}}\)

\(k={1\over{(8.50 min)(0.150M)}} = {0.7843}{ 1\over M \times min}\)

To find the time it takes for the concentration to drop to 0.0300 mol/L, we use the integrated law for second order reactions:

\({1\over[A]} = {1\over [A]_0}+ kt\)

Plug in the given values from the problem into the integrated rate law to solve for "t."

\({1\over 0.0300 M} = {1\over 0.150 M} + (0.7843 { 1\over M \times min}) t\)

\(t= {({1\over 0.0300 M} - {1\over 0.150 M} )\over 0.7843{ 1\over M \times min}} = 34 min\)

The time it takes for the concentration of compound A to drop from 0.150 mol/L to 0.0300 mol/L when the reaction is second order with respect to A is about 34 minutes.

Q21.2.6

Calculate the density of the \(^{24}_{12}Mg\) nucleus in g/mL, assuming that it has the typical nuclear diameter of \(1 × 10^{–13}\) cm and is spherical in shape.

S21.2.6

We are given the following:

Diameter= \(1\times 10^{-13}\) cm

Radius= \({{Diameter}\over 2}\)= \({{1\times 10^{-13} cm}\over 2}=5 \times 10^{-14} cm\)

Since the nucleus is spherical in shape, we can use the volume formula of a sphere to calculate the volume of the \(Mg\) nucleus.

\(V={4\over3} \pi r^3 = {4\over3} \pi (5 \times 10^{-14} cm)^3=1.67x 10^{-40} cm^3\)

Because the given the mass number for \(^{24}_{12}Mg\) nucleus is 24 amu we must convert to grams in order to determine the density in g/mL.

To calculate the density, perform the following calculations:

\(Density = {mass\over volume}\)

\( = {24 amu \times {1.66 \times 10^{-24}g \over 1 amu}}\over{1.67 \times 10^{-40} cm^3 \times{ 1 mL\over1 cm^3}}\)

\(= 2.39 x 10^{17}{ g\over mL}\)

The density of the \(^{24}_{12}Mg\) nucleus is about \(= 2.39 x 10^{17}{ g\over mL}\)

Q21.6.1

How can a radioactive nuclide be used to show that the equilibrium:

\(AgCl(s)⇌Ag^+(aq)+Cl^-(aq)\)

is a dynamic equilibrium?

S21.6.1

Radioactive nuclides can be used to test equilibrium by conducting an experiment where either one of the reactants or products consists of a radioactive nuclide. By testing the above reaction, if we add radioactive \(Ag^+\) or radioactive \(Cl^-\), both of which are on the product side, by Le Chatelier's Principle, the equilibrium shifts back to the left towards the reactant side. Given a sufficient amount of time for the reaction to reach such equilibrium, a radioactive precipitate, silver chloride, will be produced, compared with the original silver chloride precipitate that did not have radioactivity.

Q20.4.7

Identify the oxidants and the reductants in each redox reaction.

1. \(Cr(s) + Ni^{2+}(aq) → Cr^{2+}(aq) + Ni(s)\)
2. \(Cl_2(g) + Sn^{2+}(aq) → 2Cl^-(aq) + Sn{4+}(aq)\)
3. \(H_3AsO_4(aq) + 8H^+(aq) + 4Zn(s) → AsH_3(g) + 4H_2O(l) + 4Zn^{2+}(aq)\)
4. \(2NO_2(g) + 2OH^−(aq) → NO_2^−(aq) + NO_3^−(aq) + H_2O(l)\)

S20.4.7

1. oxidant: \(Ni^{2+}(aq)\); reductant: \(Cr(s)\)
2. oxidant: \(Cl_2(g)\); reductant: \(Sn^{2+}(aq)\)
3. oxidant: \(H_3AsO_4(aq)\); reductant: \(Zn(s)\)
4. oxidant: \(NO_2(g)\); reductant: \(NO_2(g)\)

An oxidant, or oxidizing agent, oxidizes other substances and gains electrons in doing so, therefore reduced in the reaction.

A reductant, or reducing agent, reduces other substances and thus loses electrons, being oxidized in the reaction.

We look at the oxidation states in each redox reaction to determine the corresponding oxidants and reductants.

In reaction 1, \(Cr\) has an oxidation state of 0, \(Ni\) has a state of +2, \(Cr\) has a state of +2, and \(Ni\) has a state of 0. From reactant to product, the oxidation state of \(Cr\) increases from 0 to +2, meaning that it loses electrons, and is therefore oxidized. So, \(Ni^{2+}\) is the oxidant that oxidizes \(Cr\), and gains electrons in doing so, so its oxidation state decrease from +2 to 0, and \(Cr\) reduces \(Ni^{2+}\) in doing so.

In reaction 2, the oxidation state of chlorine changes from 0 to -1, and the oxidation state of tin changes from +2 to +4. Chlorine gains electrons, so it is reduced, so tin reduces chlorine and is the reducing agent, while tin loses electrons, is oxidized, so chlorine oxidizes tin.

In reaction 3, the oxidation state of hydrogen stays +1 throughout the reaction. The oxidation state of \(As\) changes from +5 to -3, therefore gaining electrons, and is reduced. Zinc reduces \(H_3AsO_4\) and is therefore a reductant. The oxidation state of zinc changes from 0 to +2, therefore losing electrons, and is oxidized. \(H_3AsO_4\) oxidizes zinc and is therefore an oxidant.

In reaction 4, the oxidation state of oxygen is -2 throughout the process, as is the oxidation state of hydrogen, which is +1, so \(OH^-\) cannot be the oxidant nor the reductant. The only oxidation state that is changing is nitrogen, in which its oxidation state goes from +4 in the reactant to +3 in \(NO_2^-\) and +5 in \(NO_3^-\). Because there is both a loss and gain of electrons, \(NO_2\) is both the oxidant and the reductant.

Q20.7.5

This reaction is characteristic of a lead storage battery:

\(Pb(s) + PbO_2(s) + 2H_2SO_4(aq) \to 2PbSO_4(s) + 2H_2O(l)\)

If you have a battery with an electrolyte that has a density of 1.15 \({g\over cm^3}\) and contains 30.0% sulfuric acid by mass, is the potential greater than or less than that of the standard cell?

S20.7.5

We first look at the equations occurring at the anode and cathode.

At the anode, the following reaction is occurring:

\(Pb (s) + HSO_4^- (aq) \to PbSO_4 (s) + H^+ (aq) + 2e^-\) \(E°=-0.356 V\)

At the cathode, the following reaction is occurring:

\(2e^- + PbO_2 (s) + HSO_4^- (aq) + 3H^+ (aq) \to PbSO_4 (s) + 2H_2O (l)\) \(E°=+1.685 V\)

\(E° = E_cathode- E_anode\)= 1.685 V - (-0.356 V) = 2.041 V

Nernst Equation: \(E= E° - {RT\over nF} lnQ\)

\(E= 2.041 V - {8.3145 {J \over mol \times K} (298 K)\over 2 mol e^- \times 96485 {C\over mol e^-} } ln{1\over[H_2SO_4]^2}\)

\(E= 2.041 V - 0.01284{ln {1\over[H_2SO_4]^2}}\)

Now, solve for the unknown molarity of sulfuric acid. Given that the battery is 30.0% sulfuric acid by mass means that assuming 100 g of solution, 30 g is \(H_2SO_4\) and 70 g is water. To find the concentration, determine the number of moles of sulfuric acid and use density as a conversion factor to find the volume of the solution, then calculate the resulting molarity.

First, convert the 30 g of \(H_2SO_4\) into moles:

\({Moles H_2SO_4\over 100 g solution}={30 g H_2SO_4\over 100 g solution} \times {1 mol H_2SO_4\over 98.1 g H_2SO_4} = {{0.30581 mol H_2SO_4}\over 100 g solution}\)

Next, find the volume of 100 g of solution, using density as a conversion factor.

Volume = \(100.0 g soln \times {1 mL \over 1.15 g solution}= 86.9565 mL = 0.086957 L\)

\(Molarity of H_2SO_4 = {moles H_2SO_4\over liters of solution}={ 0.30581 mol H_2SO_4\over 0.086957 L}= 3.52 M\)

Now, plug the molarity of \(H_2SO_4\) back into the Nernst equation:

\(E= 2.041 V - 0.01284ln {1\over[H_2SO_4]^2} = 2.041 V - 0.01284ln {1\over (3.52 M)^2}\)

=2.073 V

Therefore,

\(E°\)= 2.041 V

\(E\)=2.073 V

Answer:

Because \(E> E°\), the potential is greater than that of the standard cell.