Extra Credit 1
- Page ID
- 82816
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Q17.1.1
If a 2.5 A current is run through a circuit for 35 minutes, how many coulombs of charge moved through the circuit?
S17.1.1
An electrical current is the rate of flow of charge in a circuit, where current (I) is measured in amps (A). The charge is measured in coulombs (C). We can find this charge by multiplying the current by the amount of time it runs through the circuit, therefore:
\[ \underbrace{Q}_{\text{total charge (coulombs)}} = \underbrace{I}_{\text{current(amperes)}} \times \underbrace{t}_{\text{time(seconds)}}\]
In this case our current (I) is 2.5 Amps and our time is 35 minutes.
Because the charge in coulombs is in Amps x seconds, our first step is to convert minutes to seconds:
(35 minutes)(60 seconds/minute) = 2100 seconds, so our time is 2100 seconds.
Plugging the values for current and time into the equation for electrical charge, we get
\( \underbrace{Q}_{\text{total charge}} = \underbrace{2.5}_{\text{current}} \times \underbrace{2100}_{\text{time}} = \underbrace{5250}_{\text{coloumbs}} = \underbrace{5.3\times 10^{3}}_{\text{coloumbs}}\)
Q17.7.4
A current of 2.345 A passes through the cell shown in Figure for 45 minutes. What is the volume of the hydrogen collected at room temperature if the pressure is exactly 1 atm? Assume the voltage is sufficient to perform the reduction. (Hint: Is hydrogen the only gas present above the water?)
S17.7.4
The amount of current that is allowed to flow in an electrolytic cell is related to number of moles of electrons. The number of moles of electrons can be related to the reactants and products using stoichiometry. The total charge (Q, in coulombs) is given by
\[ \underbrace{Q}_{\text{total charge (coulombs)}} = \underbrace{I}_{\text{current(amperes)}} \times \underbrace{t}_{\text{time(seconds)}} = \underbrace{n}_{\text{moles e-}} \times \underbrace{F}_{\text{Faraday Constant}} \]
We start by finding the charge for the system using:
\[ \underbrace{Q}_{\text{total charge (coulombs)}} = \underbrace{I}_{\text{current(amperes)}} \times \underbrace{t}_{\text{time(seconds)}}\]
so, first, minutes must be converted to seconds, and since
(45 minutes)(60 seconds/minute) = 2,700 seconds is our time
Now we can use our given values of current and time to solve for charge (Q).
\[ \underbrace{Q}_{\text{total charge (coulombs)}} = \underbrace{2.345}_{\text{current(amperes)}} \times \underbrace{2700}_{\text{time(seconds)}} = \underbrace{6331.5}_{\text{total charge (coulombs)}} = \underbrace{6.3 \times 10^{3}}_{\text{total charge (coulombs)}}\]
Now that we have charge we can use this value to solve for moles of electrons using equation:
\[ \underbrace{Q}_{\text{total charge (coulombs)}} = \underbrace{n}_{\text{moles e-}} \times \underbrace{F}_{\text{Faraday Constant}} \]
so,
\[ \underbrace{n}_{\text{moles e-}} = \frac{Q}{F}\]
since we have solved for charge (Q) and have known Faraday constant (F=96,485.3329 C/mol) we can use these values to solve for moles e-
\[ \underbrace{n}_{\text{moles e-}} = \frac{6.3 \times 10^{3}}{96485.3329} = \underbrace{0.065}_{\text{moles e-}}\]
Knowing the moles e-, allows us to use stoichiometry in order to solve for moles of hydrogen gas based on reaction shown in Figure.
Since hydrogen gas is at the cathode and the reaction of water splitting yields the reaction
\[2H^+(aq) + 2e^- ⟶ H_2(g)\]
at the cathode, we can use moles e- to find moles of hydrogen gas, stoichiometry yields
( 1 mole H2 (g) / 2 moles e-)(.065 moles e-) = .0325 moles hydrogen gas
Now that we have moles of hydrogen and know the environment is under standard conditions (room temperature, pressure = 1 atm) we can use the ideal gas law to find the volume of hydrogen gas from moles hydrogen gas.
\[ \underbrace{P}_{\text{Pressure (atm)}} \times \underbrace{V}_{\text{Volume(L)}} = \underbrace{n}_{\text{moles}} \times \underbrace{R}_{\text{Gas Constant ((L x atm)/(K x mol))}} \times \underbrace{T}_{\text{Temperature (K)}}\]
so using calculated and given values yields
\[ \underbrace{1}_{\text{Pressure (atm)}} \times \underbrace{V}_{\text{Volume(L)}} = \underbrace{0.0325}_{\text{moles}} \times \underbrace{0.08206}_{\text{Gas Constant ((L x atm)/(K x mol))}} \times \underbrace{298}_{\text{Temperature (K)}}\]
\[V = 0.79 Liters\]
Q19.2.1
Indicate the coordination number for the central metal atom in each of the following coordination compounds:
- \([Pt(H_2O)_2Br_2]\)
- \([Pt(NH_3)(py)(Cl)(Br)]\) (py = pyridine, C5H5N)
- \([Zn(NH_3)_2Cl_2]\)
- \([Zn(NH_3)(py)(Cl)(Br)]\)
- \([Ni(H_2O)_4Cl_2]\)
- \([Fe(en)_2(CN)_2]^+\) (en = ethylenediamine, C2H8N2)
S19.2.1
First we must identify whether or not the ligand has more than one bonded atom (bidentate/polydentate). Using the table below we are able to do this.
| Ligand | Number of bonded atoms |
|---|---|
| Ammine (NH3) | monodentate |
| Aqua (H2O) | monodentate |
| Bromo (Br) | monodentate |
| Chloro (Cl) | monodentate |
| Cyano (CN) | monodentate |
| Pyridine (C5H5N) | monodentate |
| Ethylenediamine (C2H8N2) | bidentate |
Now that we have identified the number of bonded atoms from each ligand, we can find the total amount of bonded atoms to the central metal ion, giving us the coordination number.
- \([Pt(H_2O)_2Br_2]\): We can identify the metal ion in the complex at Pt, platinum, as the other two are listed as ligands above and are nonmetallic. We can now use the number of ligands and their bonding atoms to find its coordination number. From the table above we see that H2O has only one bonding atom and Br as well. So for each Br atom we have one bonding atom, and we have two of these, yielding 2 bonding atoms, this is the same for H2O, giving us a total number of 4 bonding atoms, and therefore a coordination number of 4.
- \([Pt(NH_3)(py)(Cl)(Br)]\) (py = pyridine, C5H5N): The metal ion in this complex, similarly to the first one, can be identified as Pt, platinum. The ligands can be identified as NH3, pyridine, Cl, and Br, which are all monodentate ligands and have one bonding atom each. Since we have four ligands, each with one bonding atom, the total number of bonding atoms on the metal ion is 4, therefore the complex has a coordination number of 4.
- \([Zn(NH_3)_2Cl_2]\): The metal ion in this complex can be identified as Zn, zinc, and the ligands can be identified as NH3 and Cl. Since these two are both monodentate ligands they have one bonding atom each. Since we have a total of two NH3 and two Cl ligands, we get a total of four monodentate ligands, giving us 4 bonding atoms and a coordination number of 4.
- \([Zn(NH_3)(py)(Cl)(Br)]\): The metal ion in this complex can be identified as Zn, zinc, and the ligands can be identified as NH3, pyridine, Cl, and Br, which are all monodentate ligands and have one bonding atom each. Since we have four ligands, each with one bonding atom, the total number of bonding atoms on the metal ion is 4, therefore the complex has a coordination number of 4.
- \([Ni(H_2O)_4Cl_2]\): The metal ion in this complex can be identified as Ni, nickel, and we can now use the number of ligands and their bonding atoms to find its coordination number. From the table above we see that H2O has only one bonding atom and Cl as well. So for each Cl atom we have one bonding atom, and we have two of these, yielding 2 bonding atoms. H2O is the same, having only one bonding atom, but there are four of these. So this gives us a total number of 6 bonding atoms, and therefore a coordination number of 6.
- \([Fe(en)_2(CN)_2]^+\) (en = ethylenediamine, C2H8N2): The metal ion in this complex can be identified as Fe, iron, and the ligands can be identifies as (en) and CN. Since (en) is bidentate, meaning it has 2 bonding atoms, and there are two of these the total bonding atoms from (en) is four. Since CN is monodentate, meaning it has one bonding atom, and there are two of these, the total bonding atoms from CN ligand is two. So, the total amount of bonding atoms is 6, therefore the complex has a coordination number of 6.
S12.3.13
Nitrosyl chloride, NOCl, decomposes to NO and Cl2.
\[2NOCl(aq) + ⟶ 2NO(g) + Cl_2(g)\]
Determine the rate equation, the rate constant, and the overall order for this reaction from the following data:
| [NOCl] (M) | 0.10 | 0.20 | 0.30 |
|---|---|---|---|
| Rate (mol/L/h) | 8.0 × 10−10 | 3.2 × 10−9 | 7.2 × 10−9 |
S12.3.13
Before we can figure out the rate constant first we must first determine the basic rate equation and rate order. The basic rate equation for this reaction, where n is the rate order of NOCl and k is the rate constant, is
\[rate = k[NOCl]^n\]
since NOCl is the reactant in the reaction.
In order to figure out the order of the reaction we must find the order of [NOCl] as it is the only reactant in the reaction. To do this we must examine how the rate of the reaction changes as the [NOCl] changes.
As [NOCl] changes from 0.10 M to 0.20 M, it doubles (x2)
When [NOCl] doubles from 0.10 M to 0.20 M the rate goes from 8.0 x 10-10 to 3.2 x 10-9
(3.2 x 10-9(mol/L/h))/(8.0 x 10-10(mol/L/h)) = 4
so we conclude that as the [NOCl] doubles, the rate goes up by 4x. Since 22= 4 we can say that the order of [NOCl] is 2 so our updated rate law is
\[rate = k[NOCl]^2\]
Now that we have the order, we can substitute the first experimental values from the given table to find the rate constant, k
(8.0 x 10-10(mol/L/h)) = k(0.10 M)2 so
\[k= \dfrac{8.0 \times 10^{-10}}{ (0.10\, M)^2} = 8 \times 10^{-8} M^{-1} sec^{-1}\]
We were able to find the units of k using rate order, when the rate order is 2 units of k are M-1 x sec-1
So the rate equation is: rate = k[NOCl]2, it is second order, and k = 8 x 10-8 M-1 x sec-1
Overall rate law : \[rate = \underbrace{(8 \times 10^{-8})}_{\text{1/(M x sec)}} [NOCl]^2\]
Q12.6.5
What is the rate equation for the elementary termolecular reaction A + 2B ⟶ products? For 3A ⟶ products?
S12.6.5
Elementary refers to the order of the reactant being equal to the stoichiometric coefficient of that reactant. Termolecular refers to the reaction having an overall rate order of 3.
For A + 2B ⟶ products, since stoichiometric coefficient of A is 1, the order of [A] must be 1, since the stoichiometric coefficient of B is 2, the order of [B] must also be two. Therefore using the basic rate law of the reaction,
\(rate = k[A]^n [B]^m\) , where n is the rate order of [A], m is the rate order of [B], and k is the rate constant,
we can find the rate equation for the elementary termolecular reaction A + 2B ⟶ products to be
\(rate = k[A] [B]^2\)
this is indeed termolecular as 1+2 = 3, so the overall rate order for the reaction is 3
For 3A ⟶ products, since the stoichiometric coefficient of A is 3, the order of [A] must also be 3. Therefore using the basic rate law of the reaction
\(rate = k[A]^n\) , where n is the rate order of [A] and k is the rate constant
We find the rate equation for the elementary termolecular reaction 3A ⟶ products to be
\(rate = k[A]^3\)
this is indeed termolecular as 3=3 so the overall rate order for this reaction is 3
Q21.4.17
If 1.000 g of \(_{88}^{226}Ra\) produces 0.0001 mL of the gas \(_{86}^{222}Rn\) at STP (standard temperature and pressure) in 24 h, what is the half-life of \(_{88}^{226}Ra\) in years?
S21.4.17
Using the equation for first-order kinetics, the following equation can be derived:
\[ \ln \frac{N}{N_{o}} = -kt\]
where "N" is the amount of radioisotope remaining after time "t" has elapsed. "No" is the initial amount of radioisotope at the beginning of the period, and "k" is the rate constant for the radioisotope.
For this problem we are going to use moles for our measure of N/No , however other units of measure, such as grams, work as well as long as the two match
In this case, we must first calculate the original amount of moles of \(_{88}^{226}Ra\)
(1.000 g)(1 mole / 226 g) = 4.425 x 10-3 moles \(_{88}^{226}Ra\)
Now we must calculate the amount of moles of \(_{88}^{226}Ra\) that decay in 1 day (24 hours) by calculating the amount of moles of \(_{86}^{222}Rn\) produced
(.0001 mL)(1 L / 1000mL)(1 mole / 22.4 L (at STP)) = 4.46 x 10-9 moles \(_{86}^{222}Rn\) produced
So the amount of \(_{88}^{226}Ra\) remaining can be calculated by
(initial moles \(_{88}^{226}Ra\)) - (moles \(_{86}^{222}Rn\)n produced) = (.0044247788) - (4.464285714 x 10-9) = .0044247743 moles remaining
Now using the values of initial and remaining moles of \(_{88}^{226}Ra\) in the equation above we can solve for k getting (1/365 years = 1 day)
\[ \ln \frac{(0.0044247743)}{(0.0044247788)} = -k( \frac{1}{365})\]
\[k = \frac{(1.017 \times 10^{-6})}{.0027} = 3.71 \times 10^{-4} years^{-1}\]
We can use our calculated value of k and use the same equation to solve of the half life of \(_{86}^{222}Rn\)
Since half life infers half of \(_{86}^{222}Rn\) remains, "N/No" will be 0.5 so
\[ \ln (0.5) = -(3.71 \times 10^{-4})t\]
\[t = \frac{(-0.6931471806)}{(-3.71 \times 10^{-4})} = 1868.32 years\]
since there is only 1 significant figure given,
\[t = 2.00 \times 10^{3} years\]
Q20.3.5
One criterion for a good salt bridge is that it contains ions that have similar rates of diffusion in aqueous solution, as K+ and Cl− ions do. What would happen if the diffusion rates of the anions and cations differed significantly?
S20.3.5

As shown in the diagram above ions diffuse from the salt bridge (positive ions in the direction of electron flow, negative ions opposite of electron flow), to maintain neutrality throughout the cell. Since the purpose of a salt bridge is to maintain electrical neutrality, a salt bridge that contains anions and cations that diffuse at very different rates would not be able to do this. Because it would be unable to maintain electrical neutrality in the cell, the reaction would rapidly cease.
Q20.5.16
For each reaction, calculate E°cell and then determine ΔG°. Indicate whether each reaction is spontaneous.
- \(2Na(s) + 2H_2O(l) ⟶ 2NaOH(aq) + H_2(g)\)
- \(K_2S_2O_6(aq) + I_2(s) ⟶ 2KI(aq) + 2K_2SO_4(aq)\)
- \(Sn(s) + CuSO_4(aq) ⟶ Cu(s) + SnSO_4(aq)\)
S20.5.16
First we must identify the reduction potential of the overall reaction using the table below:
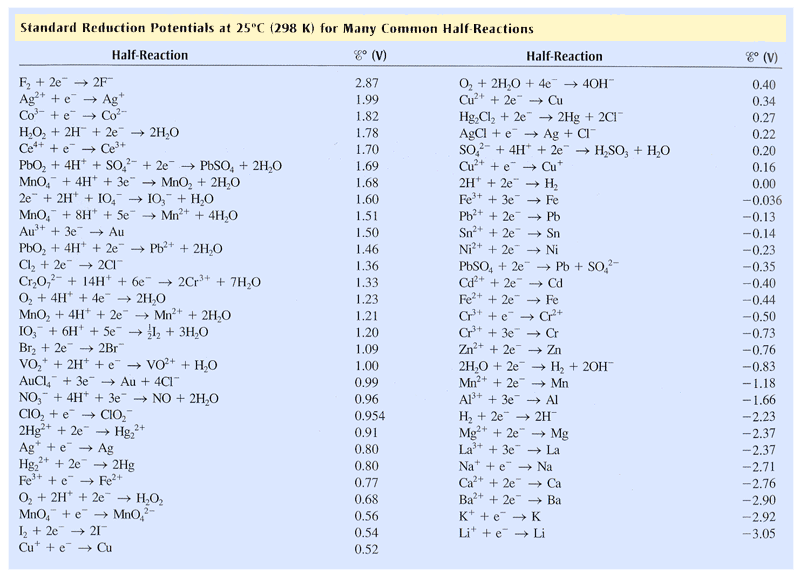
Overall cell potential is given by the equation:
\[E^{o}_{cell} = E^{o}_{cathode} - E^{o}_{anode}\]
where reduction happens at the cathode and oxidation happens at the anode
ΔG is related to the E°cell by the equation
\( \Delta G^{o}_{cell} = -nFE^{o}_{cell}\) , where n is the number of moles of electrons and F is the Faraday constant (96.485 V/mole).
1. \(2Na(s) + 2H_2O(l) ⟶ 2NaOH(aq) + H_2(g)\):
this reaction can be split up into two half reactions
cathode: \(2H_2O(l) + 2e^{-} → H_2(g) + 2OH^{-}\) E°(V)= -.083
anode: \(Na^{+} + e^{-} → Na(s)\) E°(V) = -2.71
so
\(E^{o}_{cell} = E^{o}_{cathode} - E^{o}_{anode} = {(-.083)} - {(-2.71)} = 2.627 V\)
and
\( \Delta G^{o}_{cell} = -nFE^{o}_{cell} = -(2 mole (e^{-}))(96.485 \frac{KJ}{mole e^{-} \times V})(2.627 V) = -506.93 KJ\)
since \( \Delta G^{o}_{cell}\) is negative, the reaction is spontaneous
2. \(K_2S_2O_6(aq) + I_2(s) ⟶ 2KI(aq) + 2K_2SO_4(aq)\):
the net ionic reaction (involves solid) in this case that will determine the E°cell and ΔG°cell is
\(I_2(s) + 2e^{-} → 2I^{-}(aq)\) E°(V)= 0.54
so because only iodine changes in oxidation state
\(E^{o}_{cell} = 0.54 V\)
and
\( \Delta G^{o}_{cell} = nFE^{o}_{cell} = -(2 mole (e^{-}))(96.485 \frac{KJ}{mole e^{-} \times V})(0.54 V) = -104.2 KJ\)
since ΔG°cell is negative, the reaction is spontaneous
3. \(Sn(s) + CuSO_4(aq) ⟶ Cu(s) + SnSO_4(aq)\):
this reaction can be split up into two half reactions
cathode: \(CuSO_4(aq) + 2e^{-} ⟶ Cu(s)\) E°(V)= 0.34
anode: \(Sn^{2+}(aq) + 2e^{-} → Sn(s)\) E°(V) = -0.14
so
\(E^{o}_{cell} = E^{o}_{cathode} - E^{o}_{anode} = {(0.34)} - {(-0.14)} = 0.48 V\)
and
\( \Delta G^{o}_{cell} = nFE^{o}_{cell} = -(2 mole (e^{-}))(96.485 \frac{KJ}{mole e^{-} \times V})(0.48 V) = -92.63 KJ\)
since \( \Delta G^{o}_{cell}\) is negative, the reaction is spontaneous

