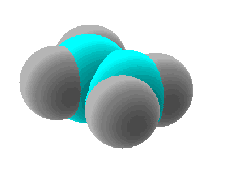Bonding and Hybridization

Chemical Bonds

Chemical bonds are the attractive forces that hold atoms together in the form of compounds. They are formed when electrons are shared between two atoms. There are 3 types of bonds...covalent bonds, polar covalent bonds and ionic bonds.

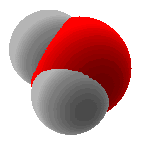
The simplest example of bonding can be demonstrated by the \(H_2\) molecule. We can see from the periodic table that each hydrogen atom has a single electron. If 2 hydrogen atoms come together to form a bond, then each hydrogen atom effectively has a share in both electrons and thus each resembles an inert gas and is more stabile. The 2 electrons that are shared can be represented either by 2 dots or a single dash between the atoms.

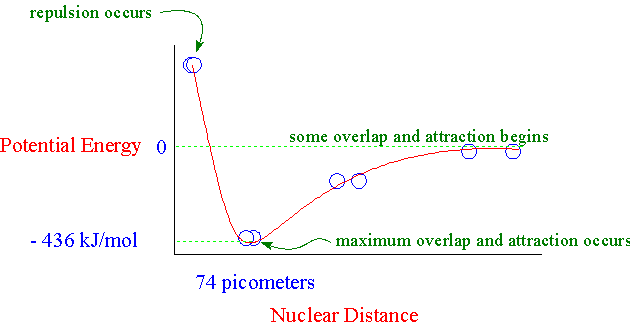
Valence bond theory describes a chemical bond as the overlap of atomic orbitals. In the case of the hydrogen molecule, the 1s orbital of one hydrogen atom overlaps with the 1s orbital of the second hydrogen atom to form a molecular orbital called a sigma bond. Attraction increases as the distance between the atoms gets closer but nuclear-nuclear repulsion becomes important if the atoms approach too close.

There are 3 methods of showing the formulas of molecules. Molecular formulas show only the types and numbers of atoms in the molecule. Structural formulas show the atoms in their correct placement in the molecule and allow for distinguishing isomers. Electron-dot formulas are similar to structural formulas but also include all of the non-bonding outer electrons. Knowledge of electron placement allows us to understand not only the shape of molecules but their chemical character. If we understand the chemical character of a molecule, we can predict how it will react with other molecules without having to blindly memorize reactions.

Drawing Electron-Dot Formulas

Let's first study the rules for drawing these structures.

1. The first electron-dot formula we will try will be \(CH_4\) (methane).
2. Now let's try a compound that has non-bonding electron pairs, \(H_2O\) (water).
3. Next we should try an ion with a negative charge, \(HO^-\) (hydroxide ion).
4. How about an ion with a positive charge, \(NH_4^+\) (ammonium ion).
5. Finally, let's draw a compound that requires multiple bonds, \(O_2\) (oxygen).

Additional Problems

Show formal charges on the atoms that have charges. When a formula contains more than a single oxygen atom, it is rare to have oxygen-oxygen bonds (except with peroxides, oxygen and ozone) so don't have your structures show oxygen-oxygen bonds. Some of these are isoelectronic species...can you pick them out?

• \(HF\) hydrogen fluoride
• \(H_2S\) hydrogen sulfide
• \(F^-\) fluoride anion
• \(Br^+\) bromine cation
• \(N_2\) nitrogen
• \(HCN\) hydrogen cyanide
• \(NC^-\) cyanide anion
• \(BF_4^-\) boron tetrafluoride anion
• \(CO\) carbon monoxide
• \(SO_4^{2-}\) sulfate anion
• \(PO_4^{3-}\) phosphate anion
• \(ClO_4^{1-}\) perchlorate anion
• \(CO_3^{2-}\) carbonate anion...Note that the bicarbonate anion looks like the carbonate with a hydrogen attached to one of the oxygen atoms.
• \(NO_3^{1-}\) nitrate anion

If you are planning to take Organic Chemistry, understanding how to draw and use electron-dot formulas is essential if you wish to succeed in this course...your understanding of reactions and reaction mechanisms, reactivity of compounds and the stereochemistry of molecules all depends on the material discussed in this tutorial.

Exceptions to the Octet Rule

It is very important that you understand the basics of what we have just covered before worrying about exceptions. In almost all cases, the elements in the first and second periods are used for electron-dot formulas. There are important exceptions but these are not as common.

Elements in groups IA, IIA and IIIA do not follow the "octet rule" that we used for the above problems. When we write the electron-dot formula for BF3, the boron will not have eight electrons and that is just fine...it helps us understand its chemical character.

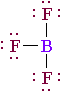
Some elements having low-energy d-orbitals also form exceptions to the "octet rule" in that more than eight electrons are accommodated around the central atom. The central atom in most of these compounds will be bonded to highly electronegative elements such as fluorine, oxygen and chlorine. A surprising element in this group is the inert gas, xenon. If xenon is exposed to fluorine gas in the presence of light for several weeks it can form \(XeF_2\), a colorless crystalline solid.

Let's try to draw the electron-dot formula for \(SF_4\) (sulfur tetrafluoride). Note that sulfur is in the 3rd period and thus does have d-orbitals available.

Transition metals offer a unique problem in that they have several common oxidation states so we tend to not write electron-dot formulas for their compounds.

Resonance

Resonance theory is one of the most important theories that helps explain many interesting aspects of chemistry ranging from differences in reactivity of related compounds to physical properties such a the absorption of light by molecules. The electron-dot formula for many of the compounds and ions presented us a choice when we placed 4 electrons between 2 of the atoms in the formation of double bonds. The carbonate and nitrate anions are examples of this problem. You may have wondered why your structure differed from the structure drawn in this tutorial in where the double bond was located. It turns out that it doesn't matter! Let's draw two electron-dot formulas for ozone, \(O_3\) placing the double bond in the 2 possible locations.

The same concept holds true for nitric acid and, in this case, the charge is evenly distributed among the 3 oxygen atoms in the nitrate anion. This makes the negative charge less available for the reverse reaction and helps explain why nitric acid is a fairly strong acid. The bond order for the nitrogen-oxygen bonds in the nitrate anion is 1.33.

Hybridization of Atomic Orbitals and the Shape of Molecules

If the four hydrogen atoms in a methane molecule (\(CH_4\)) were bound to the three 2p orbitals and the 2s orbital of the carbon atom, the H-C-H bond angles would be 90o for 3 of the hydrogen atoms and the 4th hydrogen atom would be at 135o from the others. Experimental evidence has shown that the bond angles in methane are not arranged that way but are 109.5o giving the overall shape of a tetrahedron. The tetrahedral structure makes much more sense in that hydrogen atoms would naturally repel each other due to their negative electron clouds and form this shape. If you think electron-electron repulsion isn't significant, try walking through a wall! There is plenty of space for your nuclei to pass through the nuclei of the wall material but ouch, it just doesn't work that way.

Experimental evidence has also shown that the H-N-H bond angles in ammonia (NH3) are 107o and the H-O-H bond angles in water are 105o. It is clear from these bond angles that the non-bonding pairs of electrons occupy a reasonable amount of space and are pushing the hydrogen atoms closer together compared to the angles found in methane.

The valence shell electron-pair repulsion model (VESPR) was devised to account for these molecular shapes. In this model, atoms and pairs of electrons will be arranged to minimize the repulsion of these atoms and pairs of electrons. Since the non-bonded electron pairs are held somewhat closer to the nucleus than the attached hydrogen atoms, they tend to crowd the hydrogen atoms. Thus ammonia exists as a distorted tetrahedron (trigonal pyramidal) rather than a trigonal plane and water also exists as a distorted tetrahedron (bent) rather than a linear molecule with the hydrogen atoms at a 180o bond angle.

This concept proposes that since the attached groups are not at the angles of the p orbitals and their atomic orbitals would not have maximum overlap (to form strong bonds) the s and p orbitals will be hybridized to match the bond angles of the attached groups.

The number of these new hybrid orbitals must be equal to the numbers of atoms and non-bonded electron pairs surrounding the central atom!

This valence shell repulsion model can be illustrated at home with a very fun experiment!

Example 1: Methane

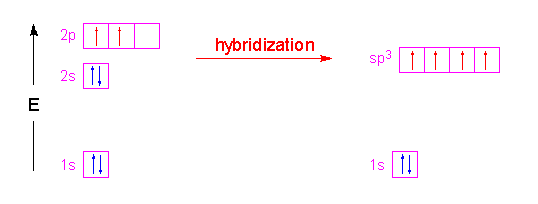
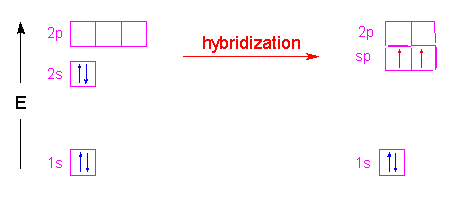
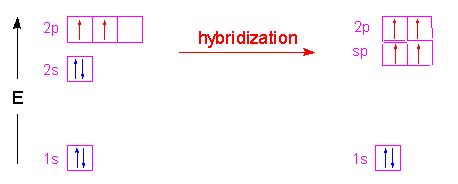
In the case of methane, the three 2p orbitals of the carbon atom are combined with its 2s orbital to form four new orbitals called "sp3" hybrid orbitals. The name is simply a tally of all the orbitals that were blended together to form these new hybrid orbitals. Four hybrid orbitals were required since there are four atoms attached to the central carbon atom. These new orbitals will have an energy slightly above the 2s orbital and below the 2p orbitals as shown in the following illustration. Notice that no change occurred with the 1s orbital. 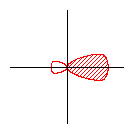These hybrid orbitals have 75% p-character and 25% s-character which gives them a shape that is shorter and fatter than a p-orbital. The new shape looks a little like... 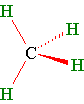A stick and wedge drawing of methane shows the tetrahedral angles...(The wedge is coming out of the paper and the dashed line is going behind the paper. The solid lines are in the plane of the paper.) A space-filling model of methane would look like...

Example 2: Ammonia

In the case of ammonia, the three 2p orbitals of the nitrogen atom are combined with the 2s orbital to form four sp3 hybrid orbitals. The non-bonded electron pair will occupy a hybrid orbital. Again we need a hybrid orbital for each atom and pair of non-bonding electrons. Ammonia has three hydrogen atoms and one non-bonded pair of electrons when we draw the electron-dot formula. In order to determine the hybridization of an atom, you must first draw the electron-dot formula. 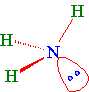A stick and wedge drawing of ammonia showing the non-bonding electrons in a probability area for the hybrid orbital... A space-filling model of ammonia would look like...(Note the non-bonded electron pair is not shown in this model.)

Example 3: Water

In the case of water, the three 2p orbitals of the oxygen atom are combined with the 2s orbital to form four \(sp^3\) hybrid orbitals. The two non-bonded electron pairs will occupy hybrid orbitals. Again we need a hybrid orbital for each atom and each pair of non-bonding electrons. Water has two hydrogen atoms and two non-bonded pairs of electrons when we draw the electron-dot formula. A stick and wedge drawing of water showing the non-bonding electron pairs in probability areas for the hybrid orbital... A space-filling model of water would look like...(Note the non-bonded electron pairs are not shown in this model.)

Example 4: Boron Trifluoride

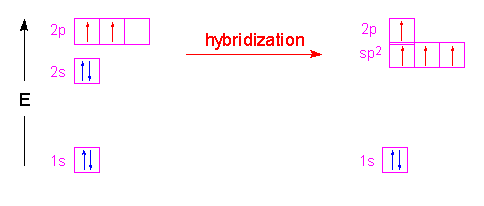
Now let's look at something a bit different. In the boron trifluoride molecule, only three groups are arranged around the central boron atom. In this case, the 2s orbital is combined with only two of the 2p orbitals (since we only need three hybrid orbitals for the three groups...thinking of groups as atoms and non-bonding pairs) forming three hybrid orbitals called \(sp^2\) hybrid orbitals. The other p-orbital remains unhybridized and is at right angles to the trigonal planar arrangement of the hybrid orbitals. The trigonal planar arrangement has bond angles of 120o. In the following stick model, the empty p orbital is shown as the probability area...one end shaded blue and the other is white...there are no electrons in this orbital! A space-filling model of boron trifluoride would look like...

Example 5: Beryllium Dichloride

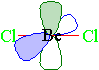
Finally let's look at beryllium dichloride. Since only two groups are attached to beryllium, we only will have two hybrid orbitals. In this case, the 2s orbital is combined with only one of the 2p orbitals to yield two sp hybrid orbitals. The two hybrid orbitals will be arranged as far apart as possible from each other with the result being a linear arrangement. The two unhybridized p-orbitals stay in their respective positions (at right angles to each other) and perpendicular to the linear molecule. In the following stick model, the empty p orbitals are shown as the probability areas...one green and one blue. A space-filling model of beryllium dichloride would look like...

Hybridization Involving d-Orbitals

As we discussed earlier, some 3rd row and larger elements can accommodate more than eight electrons around the central atom. These atoms will also be hybridized and have very specific arrangements of the attached groups in space. The two types of hybridization involved with d orbitals are \(sp^3d\) and \(sp^3d^2\).

The groups will be arranged in a trigonal bipyramidal arrangement with sp3d hybridization...bond angles will be 120o in the plane with two groups arranged vertically above and below this plane.

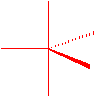
There will be an octahedral arrangement with \(sp^3d^2\) hybridization...all bond angles are at 90o.

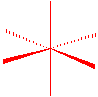
Non-bonded electron pairs are always placed where they will have the most space...in the trigonal plane for \(sp^3d\) hybridization.

Try drawing the 3-dimensional electron-dot picture for each of the following molecules...First draw an electron-dot formula. Remember to put all the extra electrons on the central atom as pairs when drawing this initial electron-dot formula. Now count the groups around the central atom. If there are six groups (Remember to count non-bonding electron pairs as groups.) it will have \(sp^3d^2\) hybridization. If it has five groups it will have \(sp^3d\) hybridization.

• \(SF_6\) sulfur hexafluoride
• \(PF_5\) phosphorus pentafluoride
• \(SF_4\) sulfur tetrafluoride
• \(ClF_3\) chlorine trifluoride
• \(XeF_2\) xenon difluoride

Summary of Hybridization

In the following summary, groups are considered to be atoms and/or pairs of electrons and hybrid orbitals are the red lines and wedges. When the octet of an element is exceeded, then hybridization will involve d-orbitals. Unhybridized p-orbitals are shown as probability areas in blue and green for \(sp\) hybridization and blue for \(sp^2\) hybridization. A single electron as found in a radical would occupy an unhybridized p-orbital.

Number of Groups Attached to a Central Atom	Description and 3-Dimensional Shape
Two Groups \[sp\]
Three Groups \[sp^2\]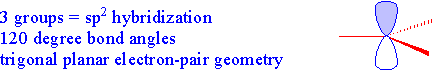
Four Groups \[sp^3\]
Five Groups \[sp^3d\]
Six Groups \[sp^3d^2\]

Hybridization Involving Multiple Bonds

Only a maximum of two electrons can occupy any orbital whether it is an atomic orbital or a molecular orbital due to electron-electron repulsion. When we draw a double or a triple-bond between two atoms, we imply that either four or six electrons are directly between these two atoms. Since this is impossible, we must have these extra electrons off to the side in what we refer to as pi bonds. Therefore, all multiple bonds are composed of two different kinds of molecular bonds called \(\pi\)-bonds and sigma-bonds.

• The \(\sigma\)-bond is defined as the linear overlap of atomic orbitals (hybrids except for hydrogen) in which two electrons are directly between the two bonded nuclei.
• \(\pi\)-bonds are defined as the parallel overlap of p-orbitals. A double bond has one sigma-bond and one pi-bond. A triple bond thus consists of a sigma-bond and two pi-bonds with the pi-bonds in different planes.

Example: Ethene

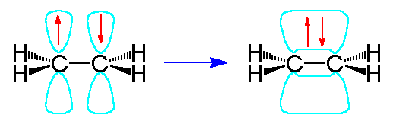
In the molecule \(C_2H_4\), ethene, both carbon atoms will be \(sp^2\) hybridized and have one unpaired electron in a non-hybridized p orbital. These p-orbitals will undergo parallel overlap and form one \(\pi\) bond with bean-shaped probability areas above and below the plane of the six atoms. This pair of bean-shaped probability areas constitutes one \(\pi\)-bond and the pair of electrons in this bond can be found in either bean-shaped area. The 3-dimensional model of ethene is therefore planar with H-C-H and H-C-C bond angles of 120o...the \(\pi\)-bond is not shown in this picture.

Example: Acetylene
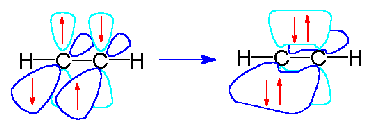
Now let's look at \(H_2C_2\) (acetylene). Both carbon atoms will be sp hybridized and have one electron in each of two unhybridized p orbitals. These p orbitals will undergo parallel overlap to form two \(\pi\)-bonds at right angles to each other. The 3-dimensional model of acetylene is therefore linear...the \(\pi\)-bonds are not shown in this picture.

Electron-Pair Geometry and Molecular Geometry

Now for a discussion about the shape of molecules! Why should you learn two ways to describe the geometry. When we experimentally look at molecules, we see how the atoms are arranged but don't see the non-bonded electron pairs. Therefore inorganic chemists tend to use molecular geometry since they deal a lot with solid ionic compounds.

When we think about the character of molecules and how they interact, those non-bonded electron pairs and their orientation in space become very important. Thus organic chemists tend to use electron-pair geometry. Since many of you will go on to take an Organic Chemistry class, you should understand both descriptions.

The various shapes for electron-pair geometry are linear, trigonal planar, tetrahedral, trigonal bipyramidal and octahedral as reviewed in the previous table. Remember a "group" is either an atom or a non-bonded pair of electrons. Some of the common shapes for molecular geometry are linear, bent, trigonal pyramidal, tetrahedral, T-shaped, seesaw and octahedral. Let's see how this works by doing some examples:

1. First draw the electron-dot formula.
2. Then determine the hybridization needed for the number of groups attached to the central atom.
3. Now draw the 3-dimensional shape corresponding to that hybridization as shown in the above table.
4. Place the non-bonded electron pairs in the most sterically open sites if the central atom has sp3d hybridization.
5. Finally describe both the electron-pair geometry and the molecular geometry.

• \(CaCl_2\) calcium chloride
• \(AlBr_3\) aluminum bromide
• \(H_3O^+\) hydronium ion
• \(H_2O\) water
• \(*CH_3\) methyl radical...There is a single unpaired electron on the carbon atom.
• \(CO_2\) carbon dioxide...What is the hybridization and geometry for each of the atoms?
• \(O_3\) ozone...What is the hybridization and geometry for each of the atoms?
• \(SF_6\) sulfur hexafluoride
• \(PF_5\) phosphorus pentafluoride
• \(SF_4\) sulfur tetrafluoride
• \(ClF_3\) chlorine trifluoride
• \(XeF_2\) xenon difluoride

Contributors

Richard Banks (Boise State University)