Electronic Spectroscopy - Interpretation
- Page ID
- 1764
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Electronic Spectroscopy relies on the quantized nature of energy states. Given enough energy, an electron can be excited from its initial ground state or initial excited state (hot band) and briefly exist in a higher energy excited state. Electronic transitions involve exciting an electron from one principle quantum state to another. Without incentive, an electron will not transition to a higher level. Only by absorbing energy, can an electron be excited. Once it is in the excited state, it will relax back to it's original more energetically stable state, and in the process, release energy as photons.
Introduction
Often, during electronic spectroscopy, the electron is excited first from an initial low energy state to a higher state by absorbing photon energy from the spectrophotometer. If the wavelength of the incident beam has enough energy to promote an electron to a higher level, then we can detect this in the absorbance spectrum. Once in the excited state, the electron has higher potential energy and will relax back to a lower state by emitting photon energy. This is called fluorescence and can be detected in the spectrum as well.
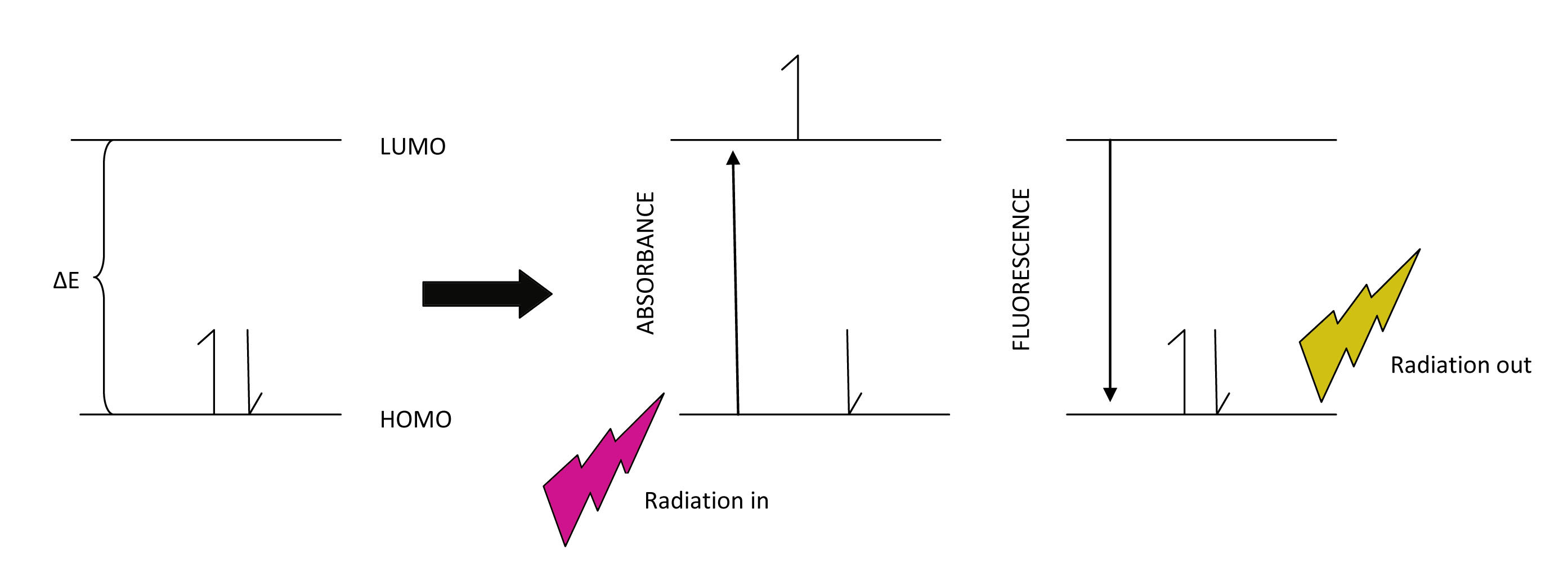
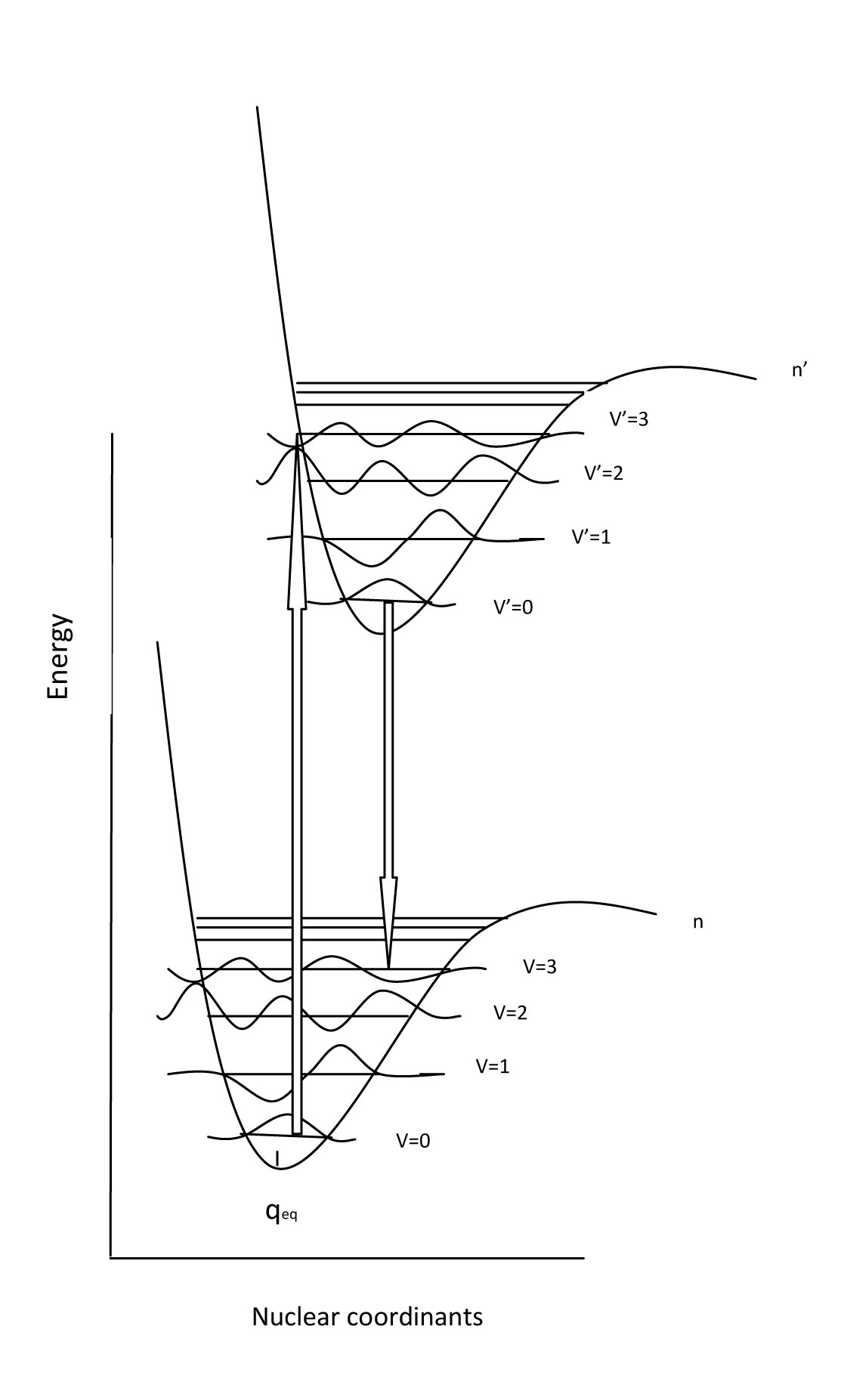
Embedded into the electronic states (n=1,2,3...) are vibrational levels (v=1,2,3...) and within these are rotational energy levels (j=1,2,3...). Often, during electronic transitions, the initial state may have the electron in a level that is excited for both vibration and rotation. In other words, n=0, v does not = 0 and r does not =0. This can be true for the ground state and the excited state. In addition, due to the Frank Condon Factor, which describes the overlap between vibrational states of two electronic states, there may be visible vibrational bands within the absorption bands. Therefore, vibrational fine structure that can be seen in the absorption spectrum gives some indication of the degree of Frank Condon overlap between electronic states.
When interpreting the absorbance and fluorescence spectra of a given molecule, compound, material, or an elemental material, understanding the possible electronic transitions is crucial. Assigning the peaks in the absorption spectrum can become easier when considering which transitions are allowed by symmetry, the Laporte Rules, electron spin, or vibronic coupling. Knowing the degree of allowedness, one can estimate the intensity of the transition, and the extinction coefficient associated with that transition. These guidelines are a few examples of the selection rules employed for interpreting the origin of spectral bands. Only a complete model of molecular energy diagrams for the species under investigation can make clear the possible electronic transitions. Every different compound will have unique energy spacing between electronic levels, and depending on the type of compound, one can categorize these spacings and find some commonality. For example, aromatic compounds pi to pi* and n to pi* transitions where as inorganic compounds can have similar transitions with Metal to Ligand Charge Transfer (MLCT) and Ligand to Metal Charge Transfer (LMCT) in addition to d-d transitions, which lead to the bright colors of transition metal complexes. Although surprises in science often lead to discovery, it is more fortuitous for the interpreter to predict the spectra rather than being baffled by the observation.
The following section will discuss the interpretation of electronic absorption spectra given the nature of the chemical species being studied. This includes an understanding of the molecular or elemental electronic state symmetries, Russell-Sanders states, spin multiplicities, and forbidden and allowed transitions of a given species.
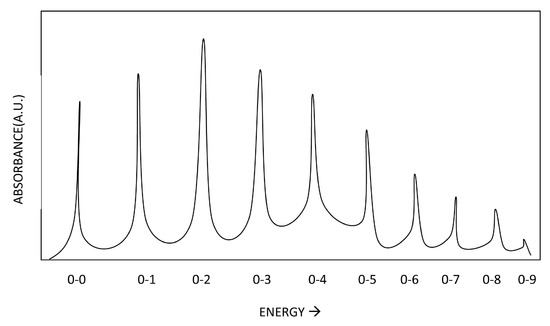
As the light passes through the monochrometer of the spectrophotometer, it hits the sample with some wavelength and corresponding energy. The ratio of the initial intensity of this light and the final intensity after passing through the sample is measured and recorded as absorbance (Abs). When absorbance is measured at different wavelengths, an absorbance spectrum of Abs vs wavelength can be obtained. This spectra reveals the wavelengths of light that are absorbed by the chemical specie, and is specific for each different chemical. Many electronic transitions can be visible in the spectrum if the energy of the incident light matches or surpasses the quantum of energy separating the ground state and that particular excited state. An example of an absorbance spectrum is given below.
Temperature Effects
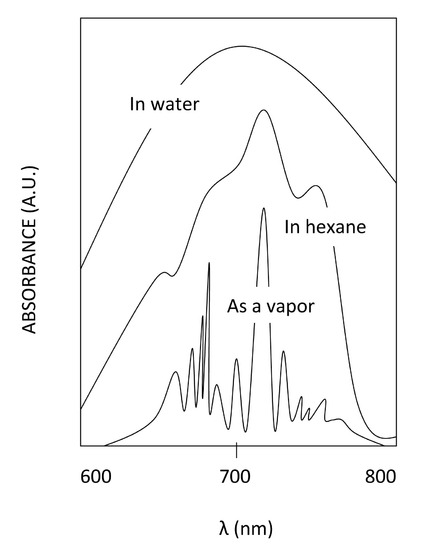
Here we can see the effect of temperature and also the effect of solvents on the clarity of the spectrum. We can see from these anonymous compounds that decreasing the temperature allows the vibrational fine structure to emerge. These vibrational bands embedded within the electronic bands represent the transitions from v=n to v'=n. Generally, the v=0 to v'=0 transition is the one with the lowest frequency. From there, increasing energy, the transitions can be from v=0 to v'=n, where n=1,2,3... With a higher temperature, the vibrational transitions become averaged in the spectrum due to the presence of vibrational hot bands and Fermi Resonance, and with this, the vibrational fine structure is lost at higher temperatures.
Solvent Effects
The effect that the solvent plays on the absorption spectrum is also very important. It is clear that polar solvents give rise to broad bands, non-polar solvents show more resolution, though, completely removing the solvent gives the best resolution. This is due to solvent-solute interaction. The solvent can interact with the solute in its ground state or excited state through intermolecular bonding. For example, a polar solvent like water has the ability of hydrogen bonding with the solute if the solute has a hydrogen bonding component, or simply through induced dipole-dipole interactions. The non-polar solvents can interact though polarizability via London interactions also causing a blurring of the vibronic manifold. This is due to the solvent's tendency to align its dipole moment with the dipole moment of the solute. Depending on the interaction, this can cause the ground state and the excited state of the solute to increase or decrease, thus changing the frequency of the absorbed photon. Due to this, there are many different transition energies that become average together in the spectra. This causes peak-broadening. The effects of peak broadening are most severe for polar solvent, less so for non-polar solvents, and absent when the solute is in vapor phase.
Group Theory and The Transition Moment Integral
When estimating the intensities of the absorption peaks, we use the molar absorptivity constant (epsilon). If the transition is "allowed" then the molar absorptivity constant from the Beer's Law Plot will be high. This means that the probability of transition is large. If the transition is not allowed, then there will be no intensity and no peak on the spectrum. Transitions can be "partially allowed" as well, and these bands appear with a lower intensity than the full allowed transitions. One way to decide whether a transition will be allowed or not is to use symmetry arguments with Group Theory.
If the symmetries of the ground and final state of a transition are correct, then the transition is symmetry allowed. We express this by modifying the transition moment integral from an integral of eigenstates to an orthogonally expressed direct product of the symmetries of the states.
\[\int \psi_{2} \mu \psi_{1} d \mathcal{T} \longrightarrow \Gamma_{2} \otimes \Gamma \mu_{x y z} \otimes \Gamma_{1} \label{1}\]
\[\int \psi_{v_{2}} \psi_{e l_{2}} \mu \psi_{v_{1}} \psi_{e l_{1}} d \mathcal{T} \longrightarrow \Gamma_{\mathrm{v}_{2}} \otimes \Gamma_{\mathrm{el}_{2}} \otimes \Gamma \mu_{x y z} \otimes \Gamma_{\mathrm{v}_{1}} \otimes \Gamma_{\mathrm{el}_{1}} \label{2}\]
The conversions of integration to direct products of symmetry as shown gives spectroscopists a short cut into deciding whether the transition will be allowed or forbidden. A transition will be forbidden if the direct products of the symmetries of the electronic states with the coupling operator is odd. More specifically, if the direct product does not contain the totally symmetric representation, then the transition is forbidden by symmetry arguments. If the product does contain the totally symmetric representation (A, A1, A1g...etc) then the transition is symmetry allowed.
Some transitions are forbidden by the Equation \ref{1} and one would not expect to be able to see the band that corresponds to the transition; however, a weak absorbance band is quite clear on the spectrum of many compounds. The transition may be forbidden via pure electronic symmetries; however, for an octahedral complex for example since it has a center of inversion, the transition is weakly allowed because of vibronic coupling. When the octahedra of a transition metal complex is completely symmetric (without vibrations), the transition cannot occur. However, when vibrations exist, they temporarily perturb the symmetry of the complex and allow the transition by equation (2). If the product of all of these representations contains the totally symmetric representation, then the transition will be allowed via vibronic coupling even if it forbidden electronically.
Hot Bands
Some transitions are forbidden by symmetry and do not appear in the absorption spectrum. If the symmetries are correct, then another state besides the ground state can be used to make the otherwise forbidden transition possible. This is accomplished by hot bands, meaning the electrons in the ground state are heated to a higher energy level that has a different symmetry. When the transition moment integral is solved with the new hot ground state, then the direct product of the symmetries may contain the totally symmetric representation. If we employ the old saying, "You can't get there from here!" then we would be referring to the transition from the ground state to the excited state. However, if we thermally excite the molecules from out of the ground state, then, "we can get there from here!"
Knowing whether a transition will be allowed by symmetry is an essential component to interpreting the spectrum. If the transition is allowed, then it should be visible with a large extinction coefficient. If it is forbidden, then it should only appear as a weak band if it is allowed by vibronic coupling. In addition to this, a transition can also be spin forbidden. The examples below of excited state symmetries, give an indication of what spin forbidden means:
.jpg?revision=1&size=bestfit&width=462&height=300)
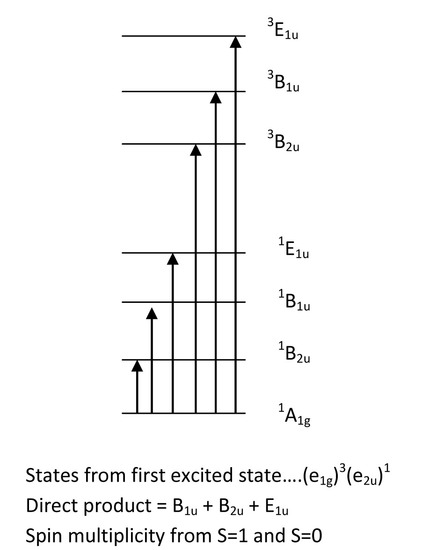
These states are derived from the electron configuration of benzene. Once we have the molecular orbital energy diagram for benzene, we can assign symmetries to each orbital arrangement of the ground state. From here, we can excite an electron from the Highest Occupied Molecular Orbital (HOMO) to the Lowest Unoccupied Molecular Orbital (LUMO). This is the lowest energy transition. Other transitions include moving the electron above the LUMO to higher energy molecular orbitals. To solve for the identity of the symmetry of the excited state, one can take the direct product of the HOMO symmetry and the excited MO symmetry. This give a letter (A, B, E..) an the subscript (1u, 2u, 1g...). The superscript is the spin multiplicity, and from single electron transitions, the spin multiplicity is 2S+1 = M, where S = 1 with two unpaired electrons having the same spin and S=0 when the excited electron flips its spin so that the two electrons have opposite spin. This gives M=1 and M=3 for benzene above. From the results above, we have three transitions that are spin allowed and three that are spin forbidden.
Once we take the direct product of the symmetries and the coupling operator for each of these states given above, we find that only the A1g to E1u transition is allowed by symmetry. Therefore, we have information regarding spin and symmetry allowedness and we have an idea of what the spectra will look like:
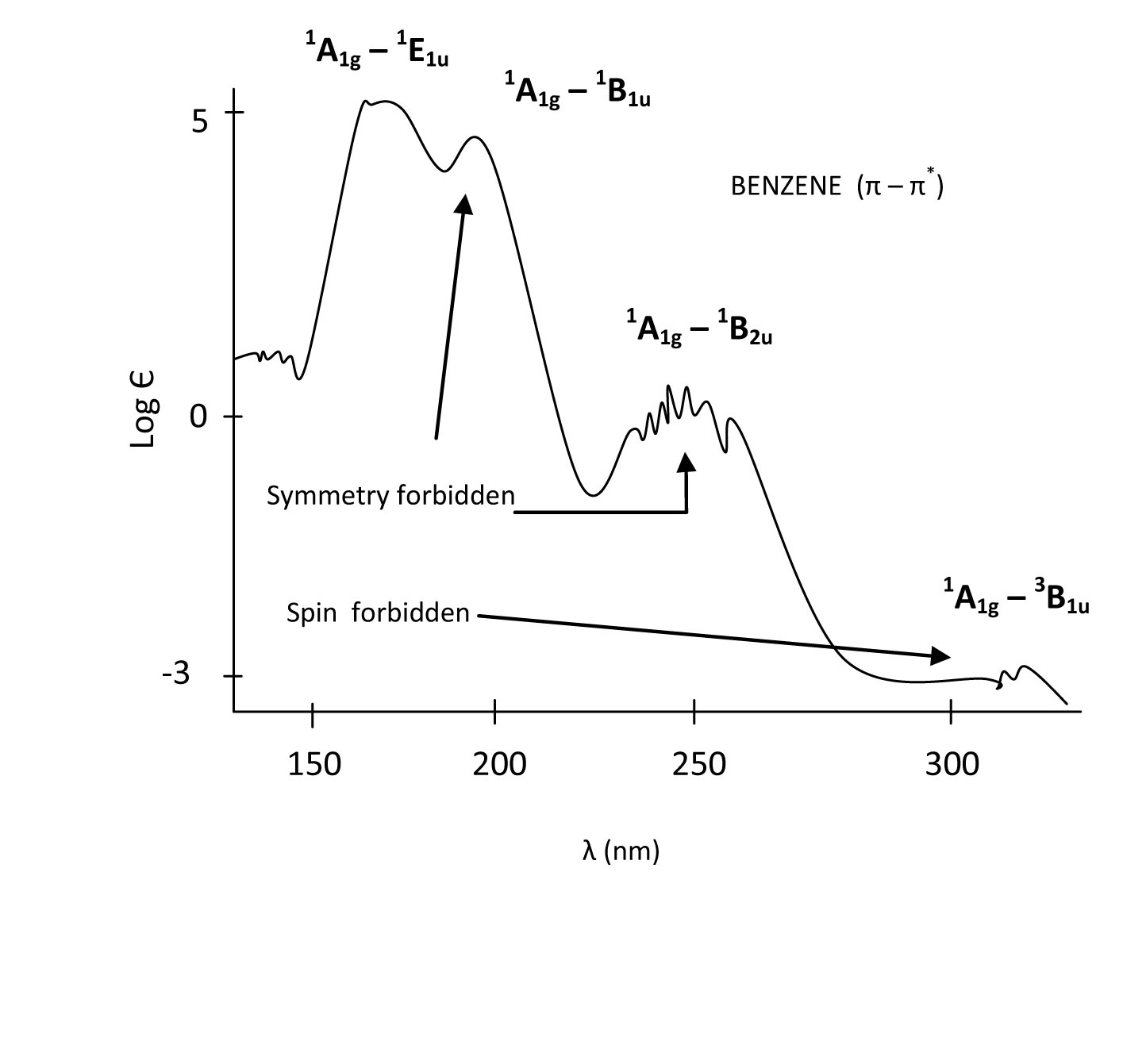
When interpreting the spectrum, it is clear that some transitions are more probable than others. According to the symmetry of excited states, we can now order them from low energy to high energy based on the position of the peaks (E1u is the highest, then B1u, and B2u is lowest). The A1g to E1u transition is fully allowed and therefore the most intense peak. The A1g to B1u and A1gto B2u transitions are symmetry forbidden and thus have a lower probability which is evident from the lowered intensity of their bands. The singlet A1g to triplet B1u transition is both symmetry forbidden and spin forbidden and therefore has the lowest intensity. This transition is forbidden by spin arguments; however, a phenomenon known as spin-orbit coupling can allow this transition to be weakly allowed as well. If spin-orbit coupling exists, then the singlet state has the same total angular momentum as the triplet state so the two states can interact. A small amount of singlet character in the triplet state leads to a transition moment integral that is non-zero, so the transition is allowed.
Organic Molecule Spectra
From the example of benzene, we have investigated the characteristic pi to pi* transitions for aromatic compounds. Now we can move to other organic molecules, which involves n to pi* as well as pi to pi*. Two examples are given below:
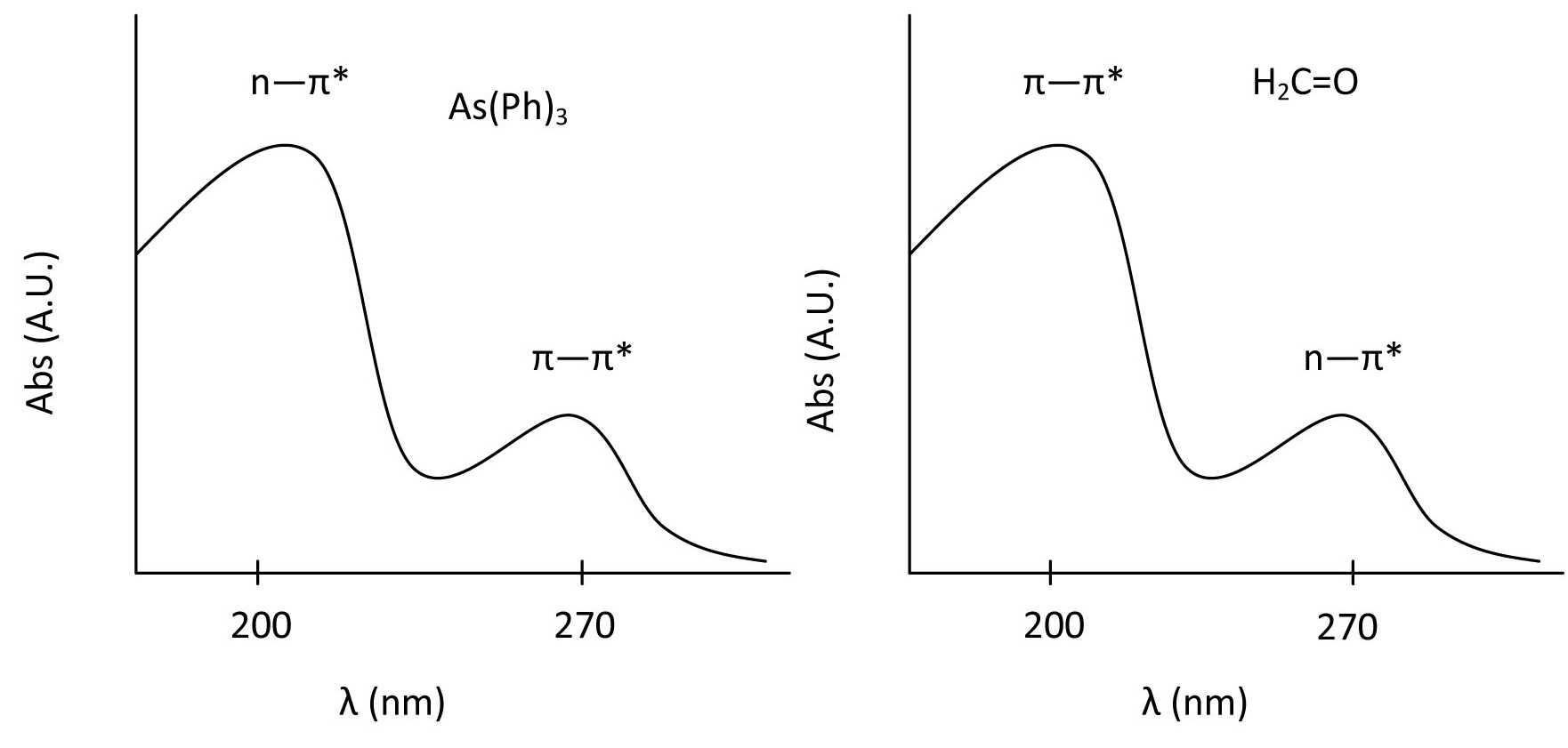
The highest energy transition for both of these molecules has an intensity around 10,000 cm-1 and the second band has an intensity of approximately 100 cm-1. In the case of formaldehyde, the \(n \rightarrow \pi^*\) transition is forbidden by symmetry where as the pi to pi* is allowed. The opposite is true for As(Ph)3 and the difference in molar absorptivity is evidence of this.
\(n \rightarrow \pi^*\) transitions
These transitions involve moving an electron from a nonbonding electron pair to a antibonding \(\pi^*\) orbital. They tend to have molar absorbtivities less than 2000 and undergo a blue shift with solvent interactions (a shift to higher energy and shorter wavelengths). This is because the lone pair interacts with the solvent, especially a polar one, such that the solvent aligns itself with the ground state. When the excited state emerges, the solvent molecules do not have time to rearrange in order to stabilize the excited state. This causes a lowering of energy of the ground state and not the excited state. Because of this, the energy of the transition increases, hence the "blue shift".
\(\pi \rightarrow \pi^*\) transitions
These transitions involve moving an electron from a bonding \(\pi\) orbital to an antibonding \(\pi^*\) orbital. They tend to have molar absorptivities on the order of 10,000 and undergo a red shift with solvent interactions (a shift to lower energy and longer wavelengths). This could either be due to a raising of the ground state energy or lowering of the excited state energy. If the excited state is polar, then it will be solvent stabilized, thus lowering its energy and the energy of the transition.
Inorganic Molecule Spectra
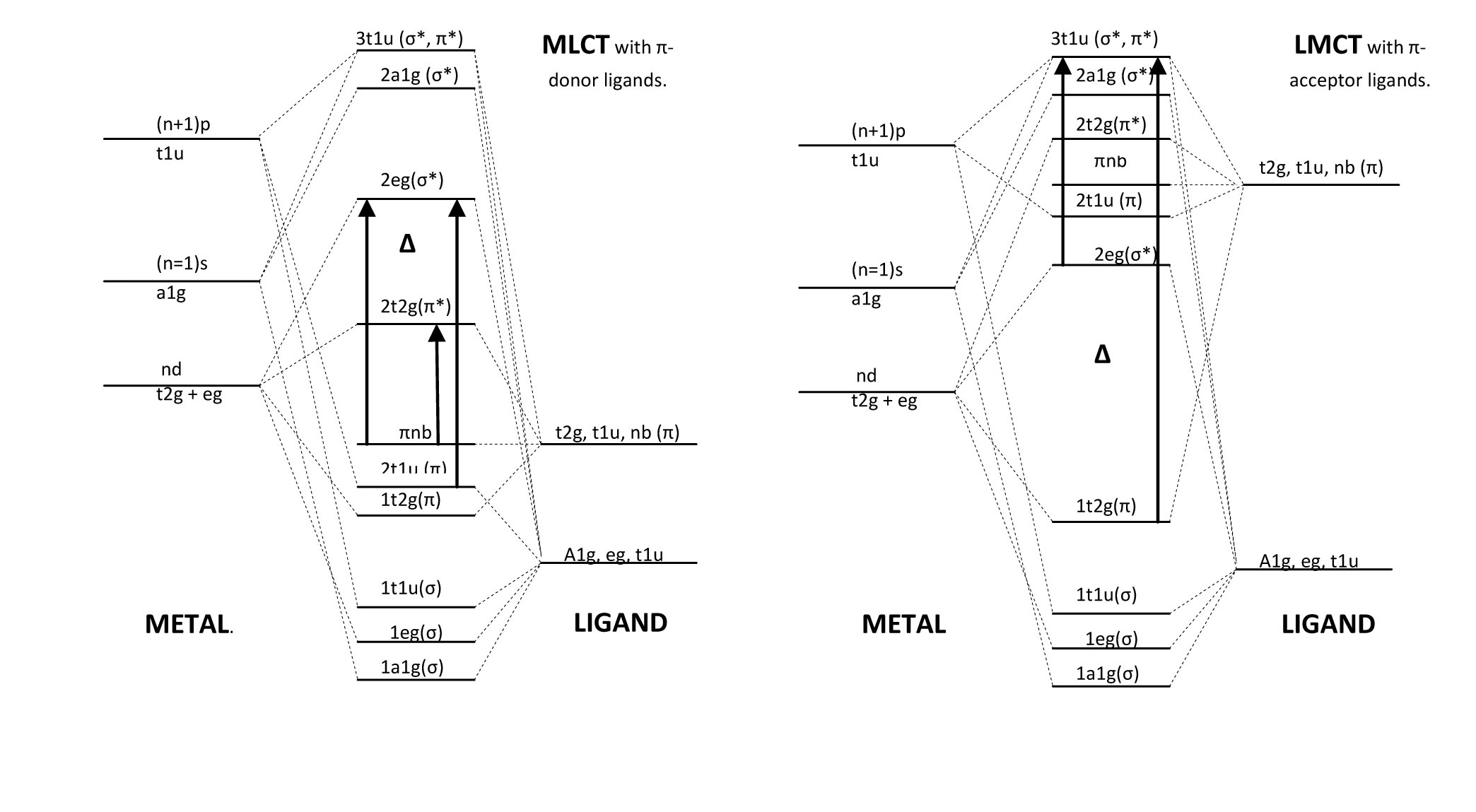
Speaking of transition probabilities in organic molecules is a good introduction to interpreting the spectra of inorganic molecules. Three types of transitions are important to consider are Metal to Ligand Charge Transfer (MLCT), Ligand to Metal Charge Transfer (LMCT), and d-d transitions. To understand the differences of these transitions we must investigate where these transitions originate. To do this, we must define the difference between pi accepting and pi donating ligands:
d-d Transitions
From these two molecular orbital energy diagrams for transition metals, we see that the pi donor ligands lie lower in energy than the pi acceptor ligands. According to the spectral chemical series, one can determine whether a ligand will behave as a pi accepting or pi donating. When the ligand is more pi donating, its own orbitals are lower in energy than the t2g metal orbitals forcing the frontier orbitals to involve an antibonding pi* (for t2g) and an antibonding sigma* (for eg). This is in contrast to the pi accepting ligands which involve a bonding pi (t2g) and an antibonding sigma* (eg). Because of this, the d-d transition (denoted above by delta) for the pi acceptor ligand complex is larger than the pi donor ligand. In the spectra, we would see the d-d transitions of pi acceptor ligands to be of a higher frequency than the pi donor ligands. In general though, these transitions appear as weakly intense on the spectrum because they are Laporte forbidden. Due to vibronic coupling; however, they are weakly allowed and because of their relatively low energy of transition, they can emit visible light upon relaxation which is why many transition metal complexes are brightly colored. The molar extinction coefficients for these transition hover around 100.
LMCT Transitions
At an even higher energy are the LMCT which involve pi donor ligands around the metal. These transitions arise because of the low-lying energy of the ligand orbitals. Therefore, we can consider this as a transition from orbitals that are ligand in character to orbitals that are more metal in character, hence the name, Ligand to Metal Charge Transfer. The electron travels from a bonding pi or non-bonding pi orbital into a sigma* orbital. These transitions are very strong and appear very intensely in the absorbance spectrum. The molar extinction coefficients for these transitions are around 104. Examples of pi donor ligands are as follows: F-, Cl-, Br-, I-, H2O, OH-, RS-, S2-, NCS-, NCO-,...
MLCT Transitions
The somewhat less common MLCT has the same intensity and energy of the LMCT as they involve the transition of an electron from the t2g (pi) and the eg (sigma*) to the t1u (pi*/sigma*). These transitions arise from pi acceptor ligands and metals that are willing to donate electrons into the orbitals of Ligand character. This is the reason that they are less frequent since metals commonly accept electrons rather than donate them. All the same, both types of Charge Transfer bands are more intense than d-d bands since they are not Laporte Rule forbidden. Examples of pi accepting ligands are as follows: CO, NO, CN-, N2, bipy, phen, RNC, C5H5-, C=C double bonds, C=C triple bonds,...
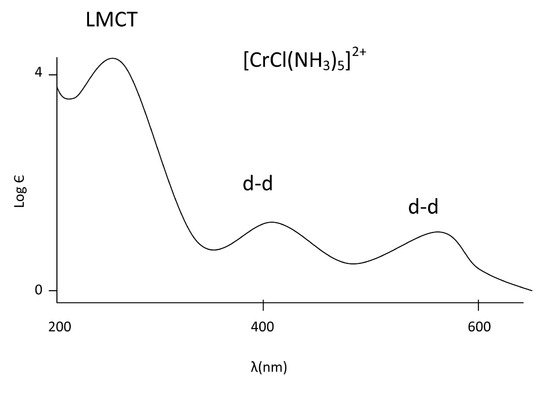 From this spectra of an octahedral Chromium complex, we see that the d-d transitions are far weaker than the LMCT. Since Chlorine is a pi donor ligand in this example, we can label the CT band as LMCT since we know the electron is transitioning from a MO of ligand character to a MO of metal character. The Laporte forbidden (symmetry forbidden) d-d transitions are shown as less intense since they are only allowed via vibronic coupling.
From this spectra of an octahedral Chromium complex, we see that the d-d transitions are far weaker than the LMCT. Since Chlorine is a pi donor ligand in this example, we can label the CT band as LMCT since we know the electron is transitioning from a MO of ligand character to a MO of metal character. The Laporte forbidden (symmetry forbidden) d-d transitions are shown as less intense since they are only allowed via vibronic coupling.
In addition, the d-d transitions are lower in energy than the CT band because of the smaller energy gap between the t2g and eg in octahedral complexes (or eg to t2g in tetrahedral complexes) than the energy gap between the ground and excited states of the charge transfer band.
These transitions abide by the same selection rules that organic molecules follow: spin selection and symmetry arguments. The Tanabe and Sugano diagrams for transition metal complexes can be a guide for determining which transitions are seen in the spectrum. We will use the [CrCl(NH3)5]2+ ion as an example for determining the types of transitions that are spin allowed. To do this we look up the Tanabe and Sugano diagrams for Octahedral fields. Since Cr in the complex has three electrons, it is a d3 and so we find the diagram that corresponds to d3 metals:
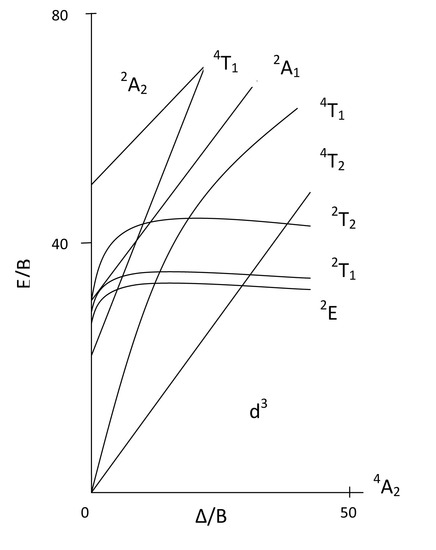
Based on the TS diagram on the left, and the information we have already learned, can you predict which transition will be spin allowed and which ones will be forbidden? From the diagram we see that the ground state is a 4A2. This is because of the three unpaired electrons which make M=2S+1= 4. The A comes from the fact that there is only one combination of electrons possible. With a spin multiplicity of 4, by the spin selection rules, we can only expect intense transitions between the ground state 4A2 and 4T2, 4T1, and the other 4T1 excited state. The other transitions are spin forbidden. Therefore, we would expect to see three d-d transitions on the absorption spectra.
For us to visualize this, we can draw these transitions in order of increasing energy and then plot the spectrum as we would expect it for only the d-d transitions in a d3 octahedral complex:
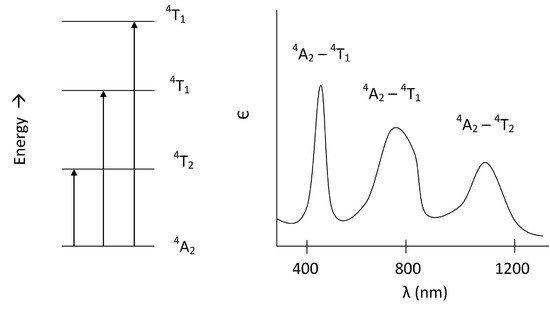
From three spin allowed transitions, we would expect to see three d-d bands appear on the spectrum. In addition to these of course, the LMCT band will appear as well.
Fluorescence
Now that we have discussed the nature of absorption involving an electron absorbing photon energy to be excited to a higher energy level, now we can discuss what happens to that excited electron. Due to its higher potential energy, the electron will relax back to its initial ground state, and in the process, emit electromagnetic radiation. The energy gap between the excited state and the state to which the electron falls determines the wavelength of light that will be emitted. This process is called fluorescence. Generally, the wavelengths of fluorescence are longer than absorbance, can you explain why? Given the following diagram, one can see that vibrational relaxation occurs in the excited electronic state such that the electronic relaxation occurs from the ground vibrational state of the excited electronic state. This causes lower energy electronic relaxations than the previous energy of absorption.
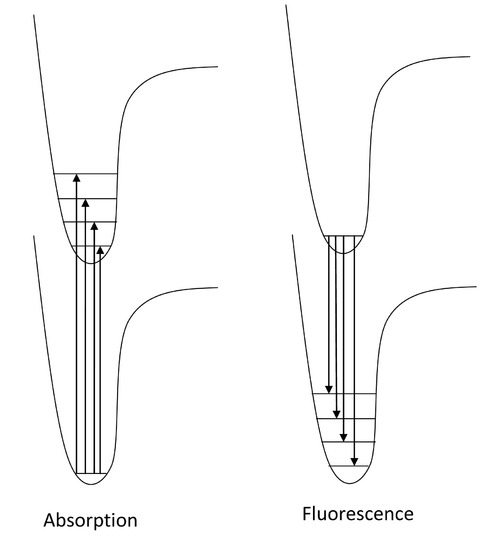
Here we see that the absorption transitions by default involve a greater energy change than the emission transitions. Due to vibrational relaxation in the excited state, the electron tends to relax only from the v'=0 ground state vibrational level. This gives emission transitions of lower energy and consequently, longer wavelength than absorption. When obtaining fluorescence, we have to block out the transmitted light and only focus on the light being emitted from the sample, so the detector is usually 90 degrees from the incident light. Because of this emission spectra are generally obtained separately from the absorption spectra; however, they can be plotted on the same graph as shown.
.jpg?revision=1&size=bestfit&width=475&height=420)
Generally separated by ~10 nm, the fluorescence peak follows the absorption peak according to the spectrum. With that, we conclude our discussion of electronic spectroscopy interpretation. Refer to outside links and references for additional information.
References
- Cotton, Albert. Chemical Applications of Group Theory. John Wiley & Sons, New York, 1990.
- Drago, Russell. Physical Methods for Chemists. Surfside Scientific Publishers, Gainesville, Fl, 1992.
- Harris, Daniel; Bertolucci, Michael. Symmetry and Spectroscopy. An Introduction to Vibrational and Electronic Spectroscopy. Dover Publications, Inc., New York, 1989.
- Miessler, Gary; Tarr, Donald. Inorganic Chemistry. Pearson Education Inc., New Jersey, 2004.
Practice Problems!
- From what we've discussed so far, if we change the solvent from non-polar to polar what effect will this have on the frequency of absorption if the ground state is non-polar and the excited state is polar? Will it increase or decrease?
- What causes peak broadening in absorption spectra?
- What are the little spikes in the more broad electronic transition bands? Draw potential energy wells to show their order and use the Frank Condon factor to describe your answer.
- Why are fluorescence bands lower in energy than absorption bands?
- If an electronic transition is symmetry forbidden and spin forbidden, list two ways of overcoming this to explain why the bands are still seen in the spectrum.
- Define MLCT, LMCT, and d-d transitions and label the molar extinction coefficients associated with each.
- How do the spectra of transition metal complexes differ with organic molecule?
- What is a "blue shift" and a "red shift" and what solvent conditions would cause these to occur?
- From the Tanabe Sugano diagram of a d2 metal complex, list all of the transitions that are spin allowed.
- Define the coupling operator that sits between the excited state wave function and the ground state wave function in the transition moment integral!

