24.4: Ideal Solutions obey Raoult's Law
- Page ID
- 14506
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Liquids tend to be volatile, and as such will enter the vapor phase when the temperature is increased to a high enough value, provided they do not decompose first. A volatile liquid is one that has an appreciable vapor pressure at the specified temperature. An ideal mixture containing at least one volatile liquid can be described using Raoult’s Law:
\[P_j = x_jP^*_j \nonumber \]
Raoult’s law can be used to predict the total vapor pressure above a mixture of two volatile liquids. As it turns out, the composition of the vapor will be different than that of the two liquids, with the more volatile compound having a larger mole fraction in the vapor phase than in the liquid phase. This is summarized in the following diagram for an ideal mixture of two compounds, water and ethanol at 75 °C. At this temperature, water a pure vapor pressure of 384 Torr and ethanol has a pure vapor pressure of 945 Torr. In Figure 24.4.1, the composition of the liquid phase is represented by the solid line and the composition of the vapor phase is represented by the dashed line.
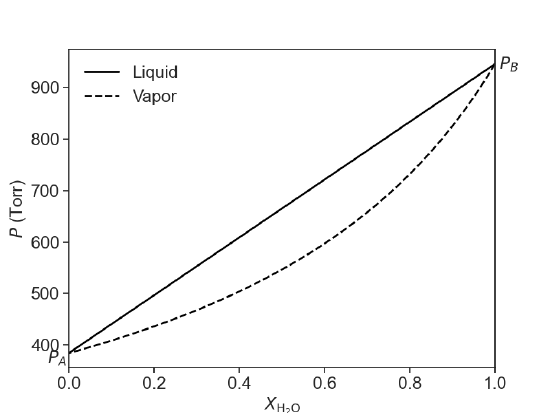
Figure 24.4.1: The composition of the liquid phase (solid line) and the vapor phase (dashed lined) as a function of mole fraction according to Raoult's law. The solution is a mixture of water and ethanol. \(P_A\) is the vapor pressure of pure water and \(P_B\) is the vapor pressure of pure ethanol at 75 °C
Often, it is desirable to depict the phase diagram at a single pressure so that temperature and composition are the variables included in the graphical representation. In such a diagram, the vapor, which exists at higher temperatures) is indicated at the top of the diagram, while the liquid is at the bottom. A typical temperature vs. composition diagram is depicted in Figure 24.4.2 for an ideal mixture of two volatile liquids.
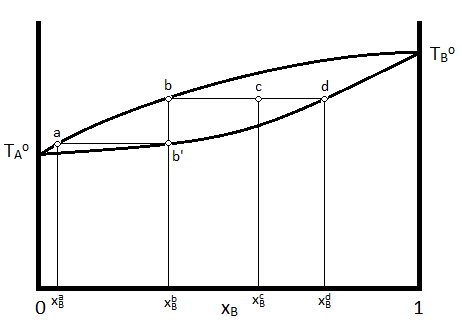
In this diagram, \(T_A\) and \(T_B\) represent the boiling points of pure compounds \(A\) and \(B\). If a system having the composition indicated by \(\chi_B^c\) has its temperature increased to that indicated by point \(c\), The system will consist of two phases, a liquid phase, with a composition indicated by \(\chi_B^d\) and a vapor phase indicated with a composition indicated by \(\chi_B^b\). The relative amounts of material in each phase can be described by the lever rule, as described previously.
Further, if the vapor with composition \(\chi_B^b\) is condensed (the temperature is lowered to that indicated by point b') and re-vaporized, the new vapor will have the composition consistent with \(\chi_B^a\). This demonstrates how the more volatile liquid (the one with the lower boiling temperature, which is \(A\) in the case of the above diagram) can be purified from the mixture by collecting and re-evaporating fractions of the vapor. If the liquid was the desired product, one would collect fractions of the residual liquid to achieve the desired result. This process is known as distillation.
The Gibbs energy of mixing is always negative
When we add \(n_A\) moles of component \(A\) and \(n_B\) moles of component \(B\) to form an ideal liquid solution, this is generally a spontaneous process. Let us consider the Gibbs free energy change of that process:
\[ \Delta_{mix}G = n_1\mu_1^{sln}+n_2\mu_2^{sln} - (n_1\mu_1^* + n_2\mu_2^*) \]
Using:
\[ \mu_i^{sln} \equiv \mu_i^* + nRTx_i\ln{x_i} \]
his expression simplifies to:
\[ \Delta_{mix} G = nRTx_A\ln{x_A} + nRTx_B\ln{x_B} \]
where \(n\) is the total moles. Mole fraction, \(x_i\), is always less than one, so the Gibbs energy of mixing is always negative; mixing is always spontaneous. We can generalize this to mixtures with more than two components:
\[ \Delta_{mix} G = nRT\sum_i{x_i\ln{x_i}} \]
This expression looks suspiciously familiar. Apart from a factor of \(-T\), it is just like the entropy of mixing:
\[ \Delta_{mix} S = -nR\sum_i{x_i\ln{x_i}} \]
Recalling the relationship between Gibbs energy and entropy:
\[ \Delta_{mix} G = \Delta_{mix}H-T\Delta_{mix}S \]
This leaves no room at all for an enthalpy effect:
\[ \Delta_{mix} H = 0 \]
Even though there are strong interactions between neighboring particles in liquids, there is no enthalpy change. This implies that it does not matter what the neighboring molecules are. If we represent the average interaction energy between molecule \(i\) and \(j\) by \(U_{ij}\), we are assuming that \(U_{ij}\) is always the same. In practice, this is seldom the case. It usually does matter and then the enthalpy term is not zero. As this affects the thermodynamics of the liquid solution, it should also affect the vapor pressures that are in equilibrium with it.
In the ideal case, volumes are additive
From the change of \(G\) in its natural variables, we know that:
\[ \left (\dfrac{\partial G}{\partial P} \right)_T =V \nonumber \]
This means that if we take
\[ \left (\dfrac{\partial \Delta G}{\partial P} \right)_T =\Delta V_{mix} \nonumber \]
In the ideal case we get:
\[ \left (\dfrac{\partial \Delta G^{ideal}}{\partial P} \right)_T =\Delta V_{mix}^{ideal} \nonumber \]
\[ \left (\dfrac{\partial RT ( n_1 \ln x_1 + n_2\ln x_2)}{\partial P} \right)_T =\Delta V_{mix}^{ideal} =0 \nonumber \]
In the ideal case, volumes are additive and we need not worry about how the partial molar volumes change with composition.

