2.1: The One-Dimensional Wave Equation
- Page ID
- 13375
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To introduce the wave equation including time and position dependence
In the most general sense, waves are particles or other media with wavelike properties and structure (presence of crests and troughs).
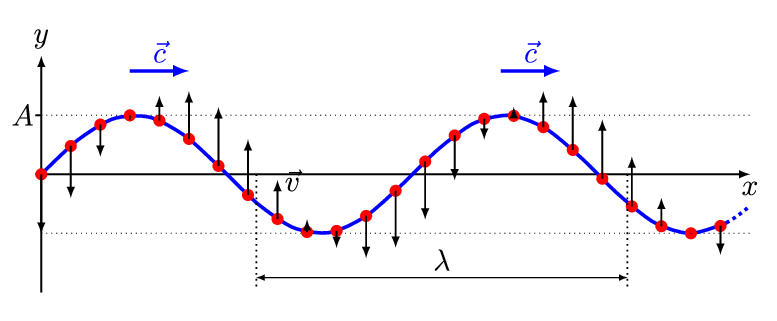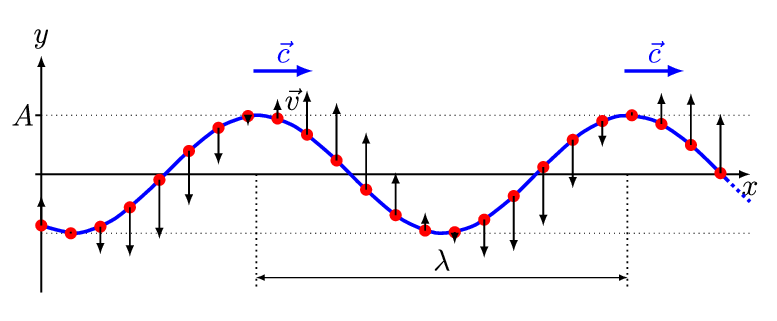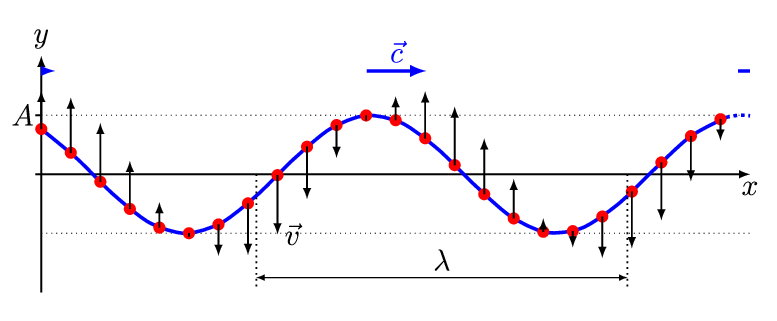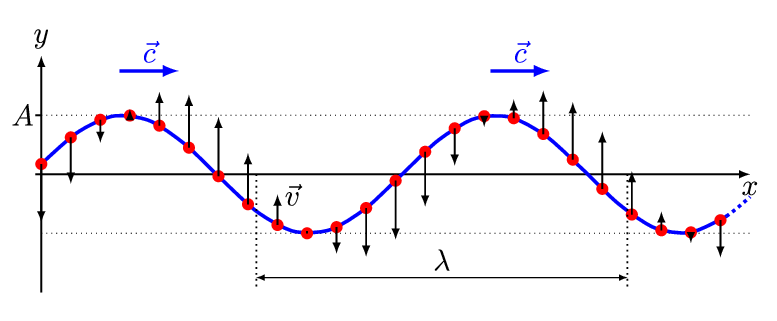
The simplest wave is the (spatially) one-dimensional sine wave (Figure 2.1.1 ) with an varing amplitude \(A\) described by the equation:
\[ A(x,t) = A_o \sin (kx - \omega t + \phi) \nonumber \]
where
- \(A_o\) is the maximum amplitude of the wave, maximum distance from the highest point of the disturbance in the medium (the crest) to the equilibrium point during one wave cycle. In Figure 2.1.1 , this is the maximum vertical distance between the baseline and the wave.
- \(x\) is the space coordinate
- \(t\) is the time coordinate
- \(k\) is the wavenumber
- \(\omega\) is the angular frequency
- \(\phi\) is the phase constant.
One can categorize “waves” into two different groups: traveling waves and stationary waves.
Traveling Waves
Traveling waves, such as ocean waves or electromagnetic radiation, are waves that “move,” meaning that they have a frequency and are propagated through time and space. Another way of describing this property of “wave movement” is in terms of energy transmission – a wave travels, or transmits energy, over a set distance. The most important kinds of traveling waves in everyday life are electromagnetic waves, sound waves, and perhaps water waves, depending on where you live. It is difficult to analyze waves spreading out in three dimensions, reflecting off objects, etc., so we begin with the simplest interesting examples of waves, those restricted to move along a line. Let’s start with a rope, like a clothesline, stretched between two hooks. You take one end off the hook, holding the rope, and, keeping it stretched fairly tight, wave your hand up and back once. If you do it fast enough, you’ll see a single bump travel along the rope:
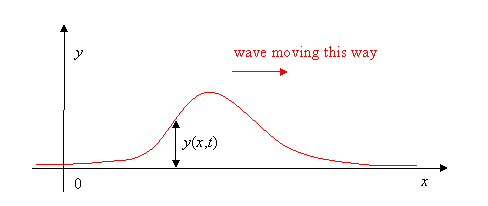
This is the simplest example of a traveling wave. You can make waves of different shapes by moving your hand up and down in different patterns, for example an upward bump followed by a dip, or two bumps. You’ll find that the traveling wave keeps the same shape as it moves down the rope. Taking the rope to be stretched tightly enough that we can take it to be horizontal, we’ll use its rest position as our x-axis (Figure 2.1.1 ). The \(y\)-axis is taken vertically upwards, and we only wave the rope in an up-and-down way, so actually \(y(x,t)\) will be how far the rope is from its rest position at \(x\) at time \(t\): that is, Figure 2.1.2 shows where the rope is at a single time \(t\).
We can now express the observation that the wave “keeps the same shape” more precisely. Taking for convenience time \(t = 0\) to be the moment when the peak of the wave passes \(x = 0\), we graph here the rope’s position at t = 0 and some later times \(t\) as a movie (Figure 2.1.3 ). Denoting the first function by \(y(x,0) = f(x)\), then the second \(y(x,t) = f(x- v t)\): it is the same function with the “same shape,” but just moved over by \(v t\), where \(v\) is the velocity of the wave.

To summarize: on sending a traveling wave down a rope by jerking the end up and down, from observation the wave travels at constant speed and keeps its shape, so the displacement y of the rope at any horizontal position at \(x\) at time \(t\) has the form
\[y(x,t)=f(x-v t) \label{2.1.0} \]
We are neglecting frictional effects—in a real rope, the bump gradually gets smaller as it moves along.
Standing Waves
In contrast to traveling waves, standing waves, or stationary waves, remain in a constant position with crests and troughs in fixed intervals. One way of producing a variety of standing waves is by plucking a melody on a set of guitar or violin strings. When placing one’s finger on a part of the string and then plucking it with another, one has created a standing wave. The solutions to this problem involve the string oscillating in a sine-wave pattern (Figure 2.1.4 ) with no vibration at the ends. There is also no vibration at a series of equally-spaced points between the ends; these "quiet" places are nodes. The places of maximum oscillation are antinodes.
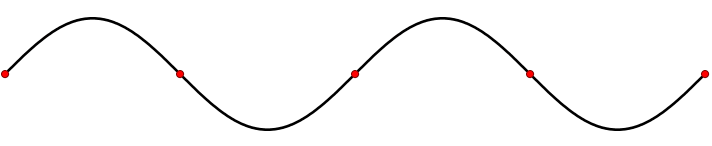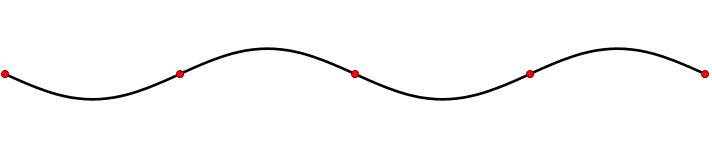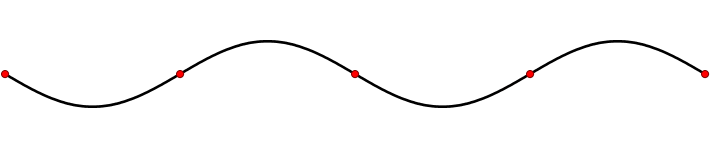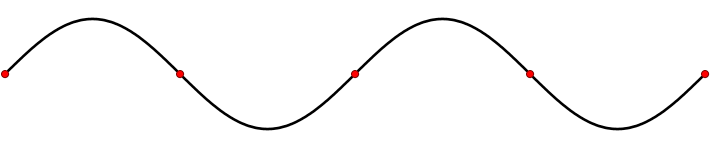
Traveling waves exhibit movement and propagate through time and space and stationary wave have crests and troughs at fixed intervals separated by nodes. "Free" particles like the photoelectron discussed in the photoelectron effect, exhibit traveling wave like properties. In contrast, electrons that are "bound" waves will exhibit stationary wave like properties. The latter was invoked for the Bohr atom for quantizing angular moment of an electron bound within a hydrogen atom.
The Wave Equation
The mathematical description of the one-dimensional waves (both traveling and standing) can be expressed as
\[ \dfrac{\partial^2 u(x,t)}{\partial x^2} = \dfrac{1}{v^2} \dfrac{\partial^2 u(x,t)}{\partial t^2} \label{2.1.1} \]
with \(u\) is the amplitude of the wave at position \(x\) and time \(t\), and \(v\) is the velocity of the wave (Figure 2.1.2 ).
Equation \(\ref{2.1.1}\) is called the classical wave equation in one dimension and is a linear partial differential equation. It tells us how the displacement \(u\) can change as a function of position and time and the function. The solutions to the wave equation (\(u(x,t)\)) are obtained by appropriate integration techniques. It may not be surprising that not all possible waves will satisfy Equation \(\ref{2.1.1}\) and the waves that do must satisfy both the initial conditions and the boundary conditions, i.e. on how the wave is produced and what is happening on the ends of the string.
For example, for a standing wave of string with length \(L\) held taut at two ends (Figure 2.1.3 ), the boundary conditions are
\[u(0,t)=0\ \label{2.1.3a} \]
and
\[u(L,t)=0 \label{2.1.3b} \]
for all values of \(t\). As expected, different system will have different boundary conditions and hence different solutions.
The initial conditions and the boundary conditions used to solve the wave equation will result in restrictions of "allowed" waves to exist in a similar fashion that only certain solutions exist for the electrons in the Bohr atom.
The first six wave solutions \(u(x,t)\) to Equation \(\ref{2.1.1}\) subject to the boundary conditions in Equations \(\ref{2.1.3a}\) and \(\ref{2.1.3b}\) (discussed in detail later) results in the wave in Figure 2.1.5 . These are standing waves that exist with frequencies based on the number of nodes (0, 1, 2, 3,...) they exhibit (more discussed in the following Section).
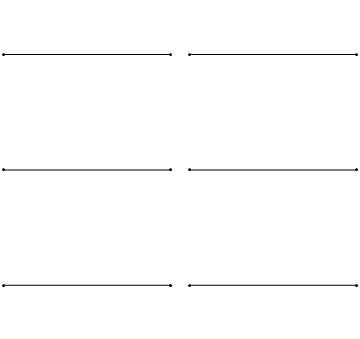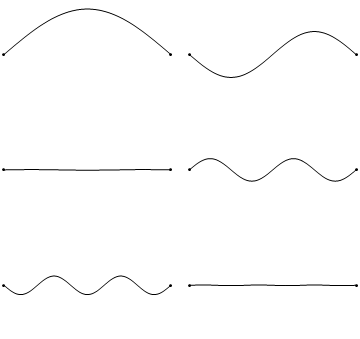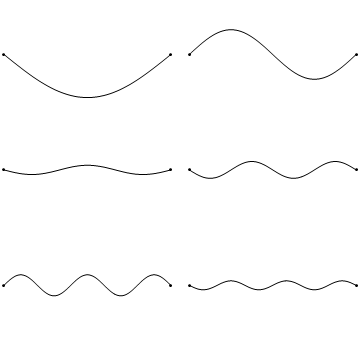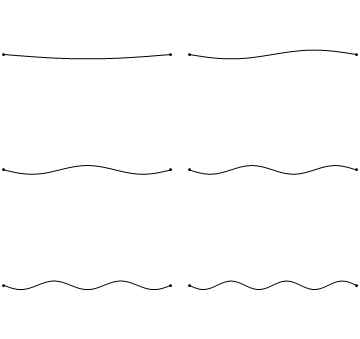
Since the acceleration of the wave amplitude (right side of Equation \(\ref{2.1.1}\)) is proportional to \(\dfrac{\partial^2}{\partial x^2}\), the greater curvature in the material produces a greater acceleration, i.e., greater changing velocity of the wave (Figure 2.1.4 ) and greater frequency of oscillation. As discussed later, the higher frequency waves (i..e, more nodes) are higher energy solutions; this as expected from the experiments discussed in Chapter 1 including Plank's equation \(E=h\nu\).
Summary
Waves which exhibit movement and are propagated through time and space. The two basic types of waves are traveling and stationary. Both exhibit wavelike properties and structure (presence of crests and troughs) which can be mathematically described by a wavefunction or amplitude function. Both wave types display movement (up and down displacement), but in different ways.Traveling waves have crests and troughs which are constantly moving from one point to another as they travel over a length or distance. In this way, energy is transmitted along the length of a traveling wave. In contrast, standing waves have nodes at fixed positions; this means that the wave’s crests and troughs are also located at fixed intervals. Therefore, standing waves only experience vibrational movement (up and down displacement) on these set intervals - no movement or energy travels along the length of a standing wave.
Contributors and Attributions
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)

