5.P: Problems for Chapter 5

Last updated
Save as PDF

Page ID: 1064

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\dsum}{\displaystyle\sum\limits} \)

\( \newcommand{\dint}{\displaystyle\int\limits} \)

\( \newcommand{\dlim}{\displaystyle\lim\limits} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\(\newcommand{\longvect}{\overrightarrow}\)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Link to Solution Manual

P5.1: For each molecule, predict the number of signals in the ¹H-NMR and the ¹³C-NMR spectra (do not count split peaks - eg. a quartet counts as only one signal). Assume that diastereotopic groups are non-equivalent.

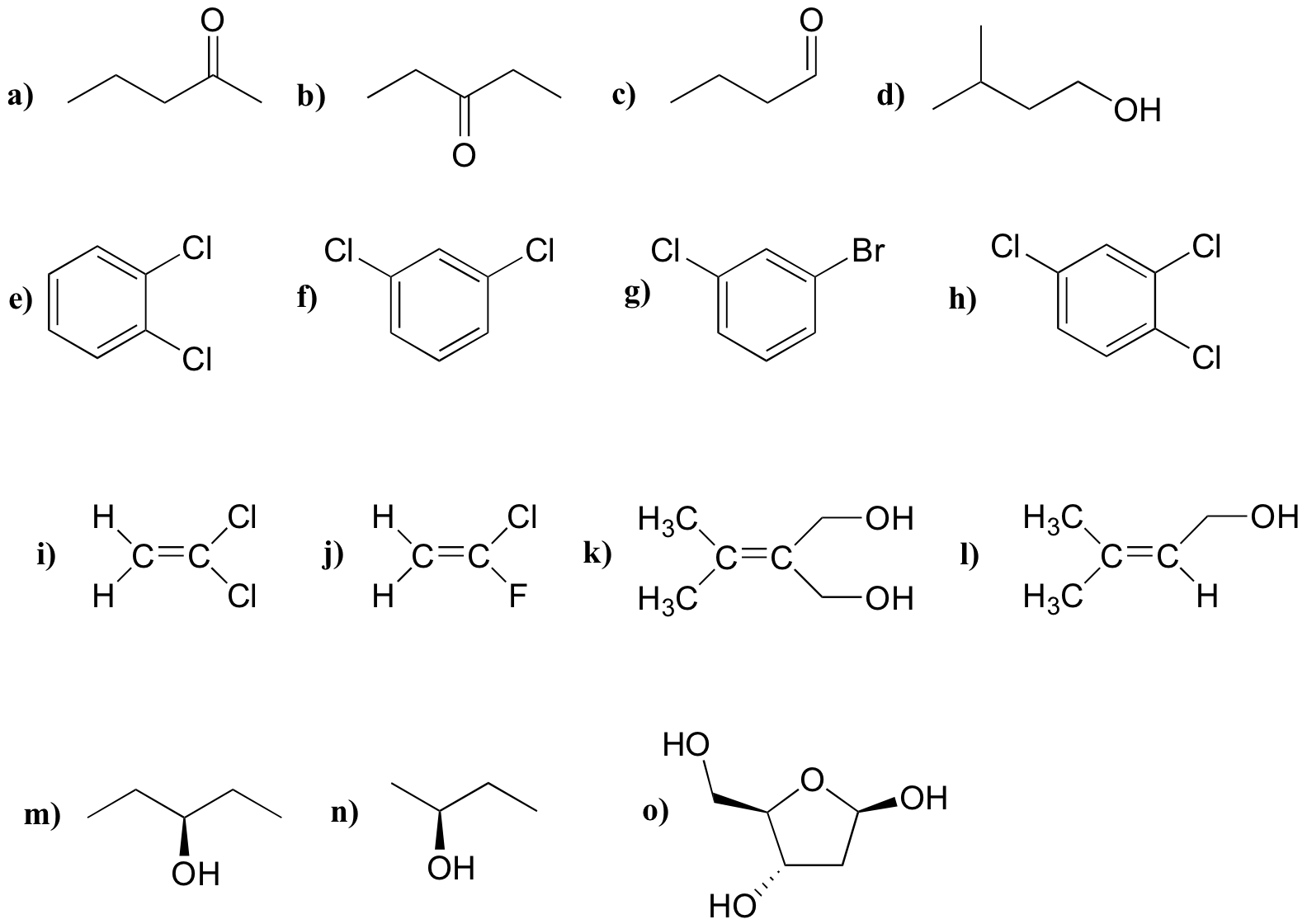
P5.2: For each of the 20 common amino acids, predict the number of signals in the proton-decoupled ¹³C-NMR spectrum.

P5.3: Calculate the chemical shift value (expressed in Hz, to one decimal place) of each sub-peak on the ¹H-NMR doublet signal below. Do this for:

a) a spectrum obtained on a 300 MHz instrument

b) a spectrum obtained on a 100 MHz instrument

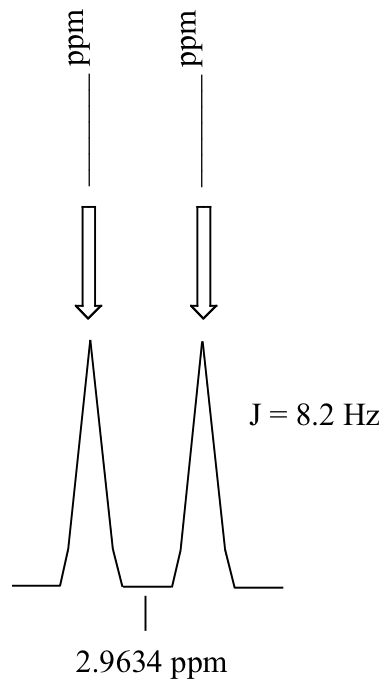
P5.4: Consider a quartet signal in an ¹H-NMR spectrum obtained on a 300 MHz instrument. The chemical shift is recorded as 1.7562 ppm, and the coupling constant is J = 7.6 Hz. What is the chemical shift, expressed to the nearest 0.1 Hz, of the furthest downfield sub-peak in the quartet? What is the resonance frequency (again expressed in Hz) of this sub-peak?)

P5.5: One easily recognizable splitting pattern for the aromatic proton signals from disubstituted benzene structures is a pair of doublets. Does this pattern indicate ortho, meta, or para substitution?

P5.6 :Match spectra below to their corresponding structures A-F.

Structures:

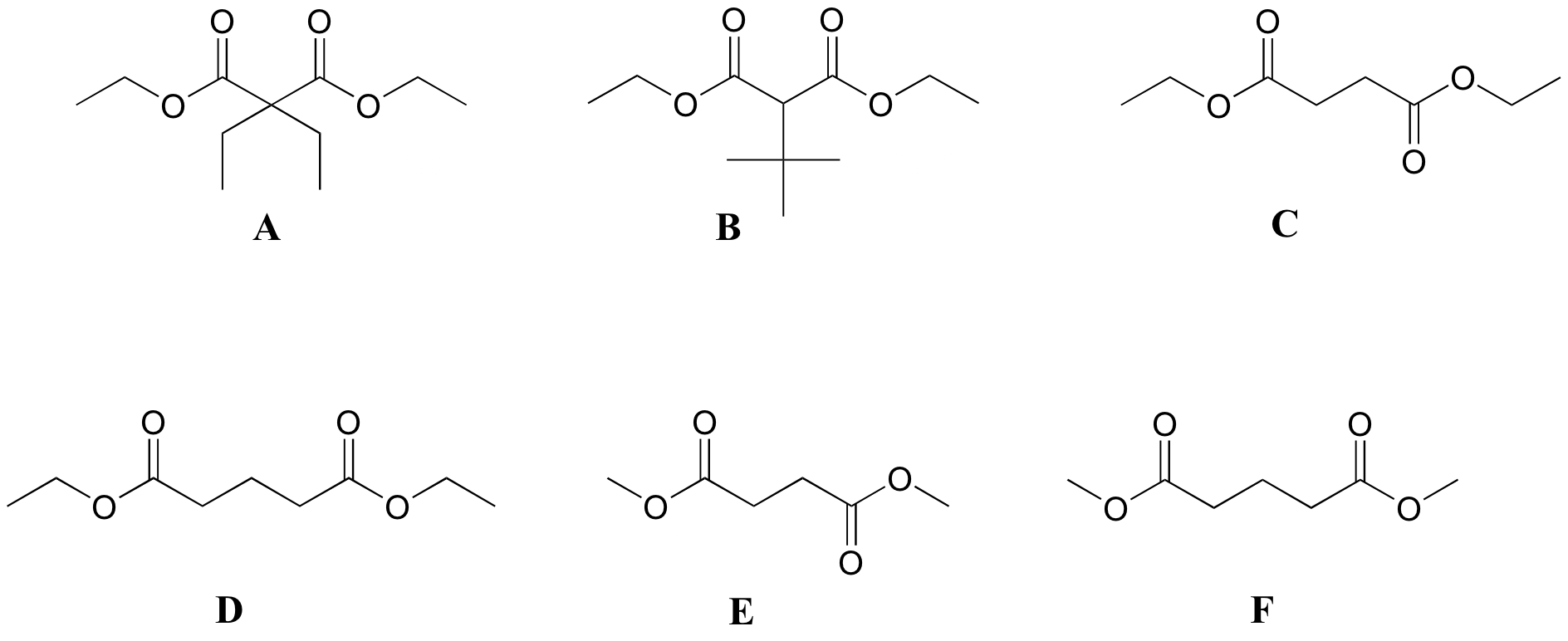
Spectrum 1

δ	splitting	integration
4.13	q	2
2.45	t	2
1.94	quintet	1
1.27	t	3

Spectrum 2

δ	splitting	integration
3.68	s	3
2.99	t	2
1.95	quintet	1

Spectrum 3

δ	splitting	integration
4.14	q	1
2.62	s	1
1.26	t	1.5

Spectrum 4

δ	splitting	integration
4.14	q	4
3.22	s	1
1.27	t	6
1.13	s	9

Spectrum 5

δ	splitting	integration
4.18	q	1
1.92	q	1
1.23	t	1.5
0.81	t	1.5

Spectrum 6

δ	splitting	integration
3.69	s	1.5
2.63	s	1

P5.7: Match spectra 7-12 below to their corresponding structures G-L .

Structures:

Spectrum 7:

δ	splitting	integration
9.96	d	1
5.88	d	1
2.17	s	3
1.98	s	3

Spectrum 8:

δ	splitting	integration
9.36	s	1
6.55	q	1
2.26	q	2
1.99	d	3
0.96	t	3

Spectrum 9:

δ	splitting	integration
9.57	s	1
6.30	s	1
6.00	s	1
1.84	s	3

Spectrum 10:

δ	splitting	integration
9.83	t	1
2.27	d	2
1.07	s	9

Spectrum 11:

δ	splitting	integration
9.75	t	1
2.30	dd	2
2.21	m	1
0.98	d	6

Spectrum 12:

δ	splitting	integration
8.08	s	1
4.13	t	2
1.70	m	2
0.96	t	3

P5.8: Match the ¹H-NMR spectra 13-18 below to their corresponding structures M-R .

Structures:

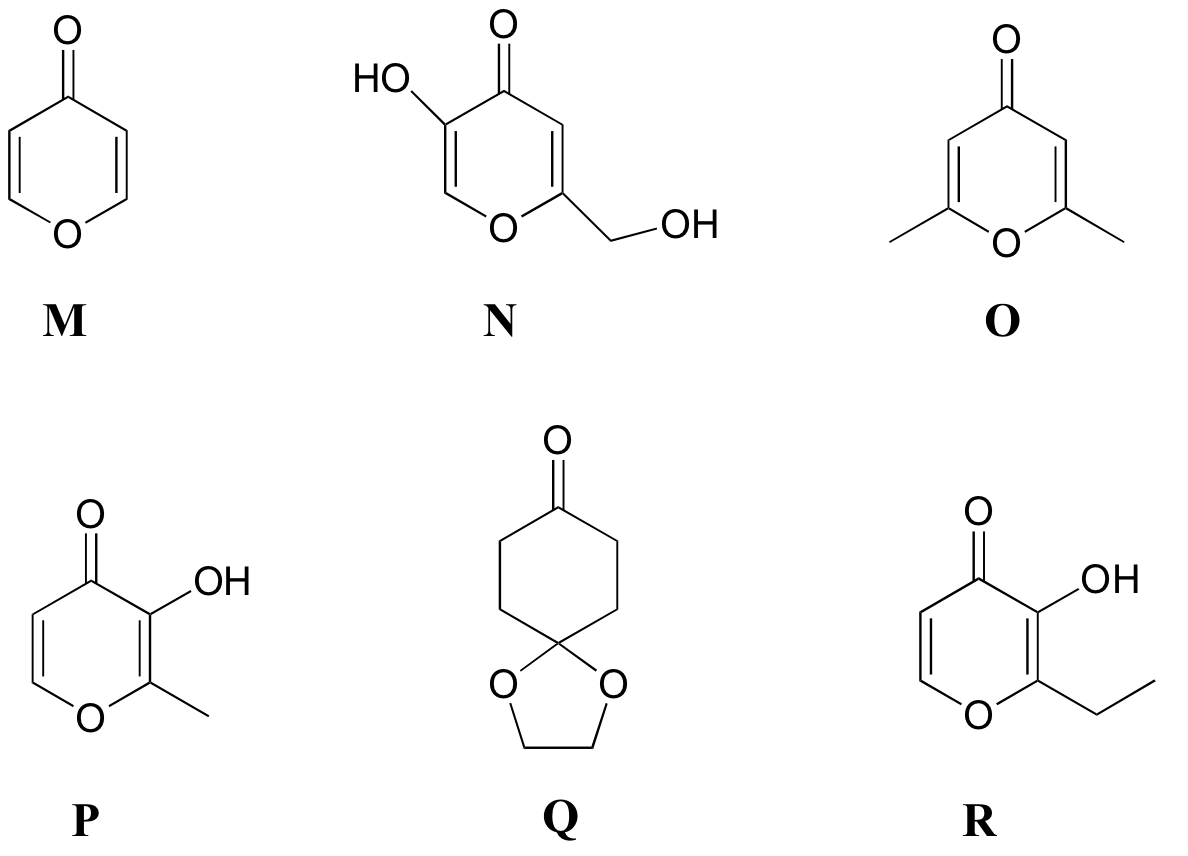
Spectrum 13:

δ	splitting	integration
8.15	d	1
6.33	d	1

Spectrum 14: 1-723C (structure O)

δ	splitting	integration
6.05	s	1
2.24	s	3

Spectrum 15:

δ	splitting	integration
8.57	s (b)	1
7.89	d	1
6.30	d	1
2.28	s	3

Spectrum 16:

δ	splitting	integration
9.05	s (b)	1
8.03	s	1
6.34	s	1
5.68	s (b)	1
4.31	s	2

Spectrum 17:

δ	splitting	integration
7.76	d	1
7.57	s (b)	1
6.44	d	1
2.78	q	2
1.25	t	3

Spectrum 18:

δ	splitting	integration
4.03	s	1
2.51	t	1
2.02	t	1

P5.9: Match the ¹H-NMR spectra 19-24 below to their corresponding structures S-X.

Structures:

Spectrum 19:

δ	splitting	integration
9.94	s	1
7.77	d	2
7.31	d	2
2.43	s	3

Spectrum 20:

δ	splitting	integration
10.14	s	2
8.38	s	1
8.17	d	2
7.75	t	1

Spectrum 21:

δ	splitting	integration
9.98	s	1
7.81	d	2
7.50	d	2

Spectrum 22:

δ	splitting	integration
7.15-7.29	m	2.5
2.86	t	1
2.73	t	1
2.12	s	1.5

Spectrum 23:

δ	splitting	integration
7.10	d	1
6.86	d	1
3.78	s	1.5
3.61	s	1
2.12	s	1.5

Spectrum 24:

δ	splitting	integration
7.23-7.30	m	1
3.53	s	1

P5.10: Match the ¹H-NMR spectra 25-30 below to their corresponding structures AA-FF.

Structures:

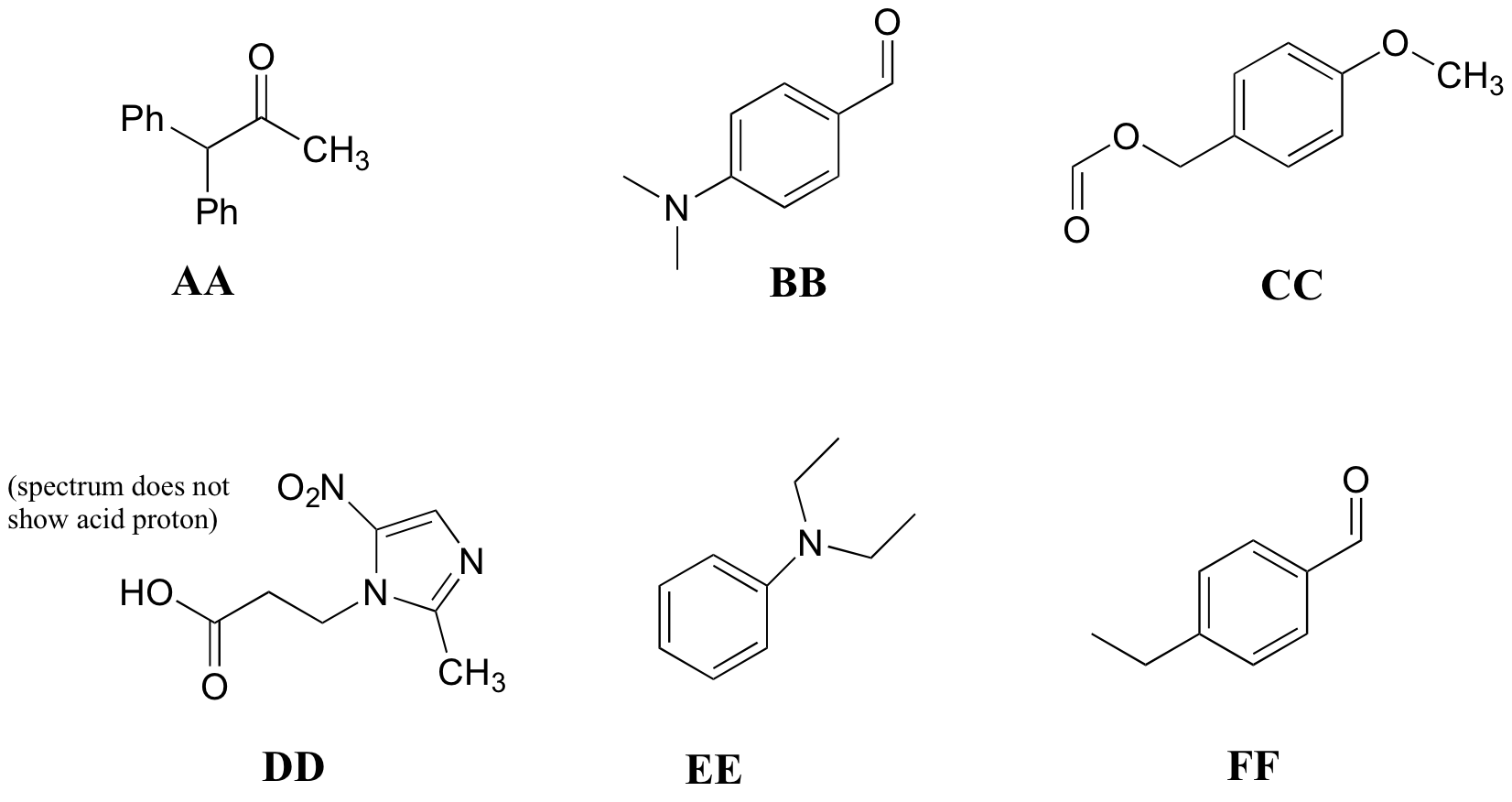
Spectrum 25:

δ	splitting	integration
9.96	s	1
7.79	d	2
7.33	d	2
2.72	q	2
1.24	t	3

Spectrum 26:

δ	splitting	integration
9.73	s	1
7.71	d	2
6.68	d	2
3.06	s	6

Spectrum 27:

δ	splitting	integration
7.20-7.35	m	10
5.12	s	1
2.22	s	3

Spectrum 28:

δ	splitting	integration
8.08	s	1
7.29	d	2
6.87	d	2
5.11	s	2
3.78	s	3

Spectrum 29:

δ	splitting	integration
7.18	d	1
6.65	m	1.5
3.2	q	2
1.13	t	3

Spectrum 30:

δ	splitting	integration
8.32	s	1
4.19	t	2
2.83	t	2
2.40	s	3

P5.11: Match the ¹H-NMR spectra 31-36 below to their corresponding structures GG-LL

Structures:

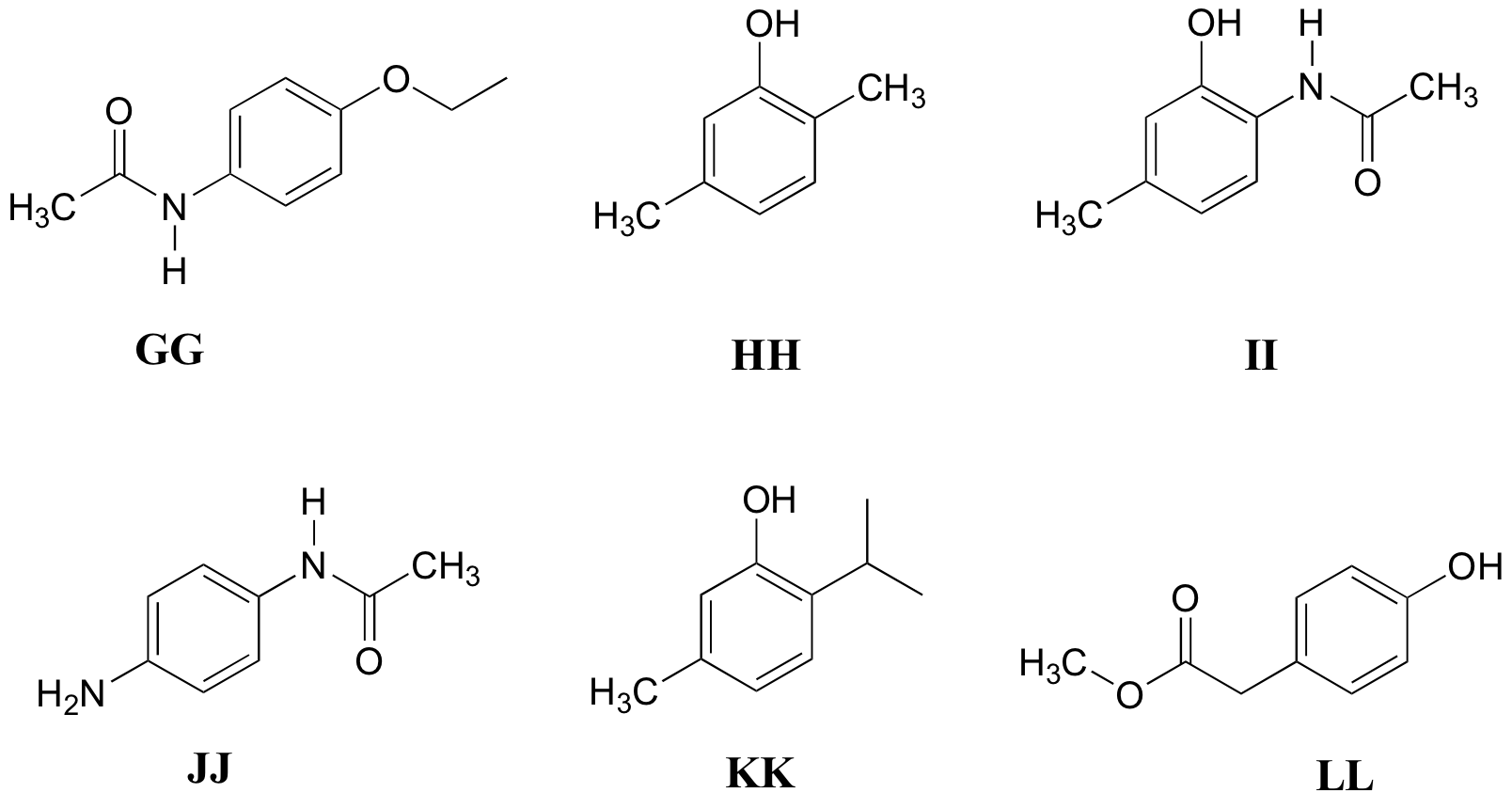
Spectrum 31:

δ	splitting	integration
6.98	d	1
6.64	d	1
6.54	s	1
4.95	s	1
2.23	s	3
2.17	s	3

Spectrum 32:

δ	splitting	integration
7.08	d	1
6.72	d	1
6.53	s	1
4.81	s	1
3.15	7-tet	1
2.24	s	3
1.22	d	6

Spectrum 33:

δ	splitting	integration
7.08	d	2
6.71	d	2
6.54	s	1
3.69	s	3
3.54	s	2

Spectrum 34:

δ	splitting	integration
9.63	s	1
7.45	d	2
6.77	d	2
3.95	q	2
2.05	s	3
1.33	t	3

Spectrum 35:

δ	splitting	integration
9.49	s	1
7.20	d	2
6.49	d	2
4.82	s	2
1.963	s	3

Spectrum 36:

δ	splitting	integration
9.58	s(b)	1
9.31	s	1
7.36	d	1
6.67	s	1
6.55	d	1
2.21	s	3
2.11	s	3

P5.12: Use the NMR data given to deduce structures.

a ) Molecular formula: C₅H₈O

¹H-NMR:

δ	splitting	integration
9.56	s	1
6.25	d (J~1 Hz)	1
5.99	d (J~1 Hz)	1
2.27	q	2
1.18	t	3

¹³C-NMR

δ	DEPT
194.60	CH
151.77	C
132.99	CH₂
20.91	CH₂
11.92	CH₃

b) Molecular formula: C₇H₁₄O₂

¹H-NMR:

δ	splitting	integration
3.85	d	2
2.32	q	2
1.93	m	1
1.14	t	3
0.94	d	6

¹³C-NMR

δ	DEPT
174.47	C
70.41	CH₂
27.77	CH
27.64	CH₂
19.09	CH₃
9.21	CH₃

c) Molecular formula: C₅H₁₂O

¹H-NMR:

δ	splitting	integration
3.38	s	2H
2.17	s	1H
0.91	s	9H

¹³C-NMR

δ	DEPT
73.35	CH₂
32.61	C
26.04	CH₃

d) Molecular formula: C₁₀H₁₂O

¹H-NMR:

δ	splitting	integration
7.18-7.35	m	2.5
3.66	s	1
2.44	q	1
1.01	t	1.5

¹³C-NMR

δ	DEPT
208.79	C
134.43	C
129.31	CH
128.61	CH
126.86	CH
49.77	CH₂
35.16	CH₂
7.75	CH₃

P5.13:

¹³C-NMR data is given for the molecules shown below. Complete the peak assignment column of each NMR data table.

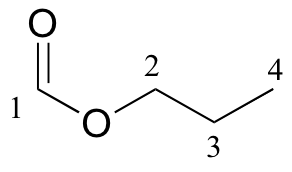
δ	DEPT	carbon #
161.12	CH
65.54	CH₂
21.98	CH₂
10.31	CH₃

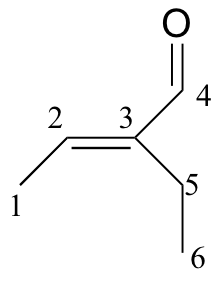
δ	DEPT	carbon #
194.72	C
149.10	C
146.33	CH
16.93	CH₂
14.47	CH₃
12.93	CH₃

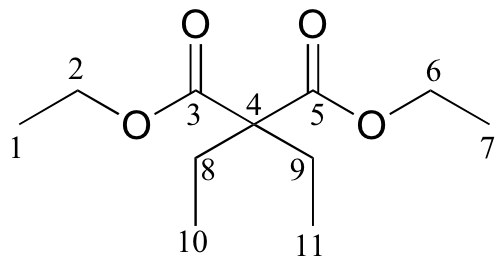
δ	DEPT	carbon #
171.76	C
60.87	CH₂
58.36	C
24.66	CH₂
14.14	CH₃
8.35	CH₃

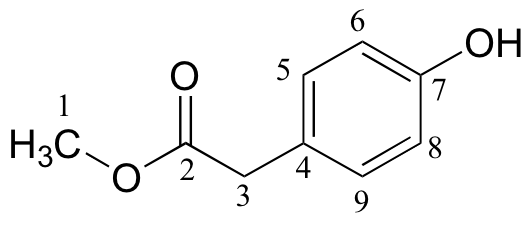
δ	DEPT	carbon #
173.45	C
155.01	C
130.34	CH
125.34	C
115.56	CH
52.27	CH₃
40.27	CH₂

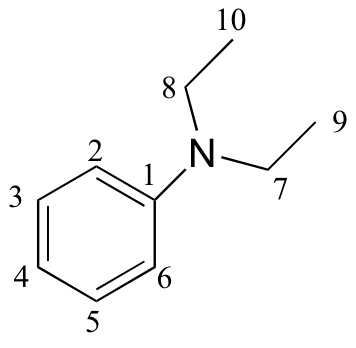
δ	DEPT	carbon #
147.79	C
129.18	CH
115.36	CH
111.89	CH
44.29	CH₂
12.57	CH₃

P5.14: You obtain the following data for an unknown sample. Deduce its structure.

¹H-NMR:

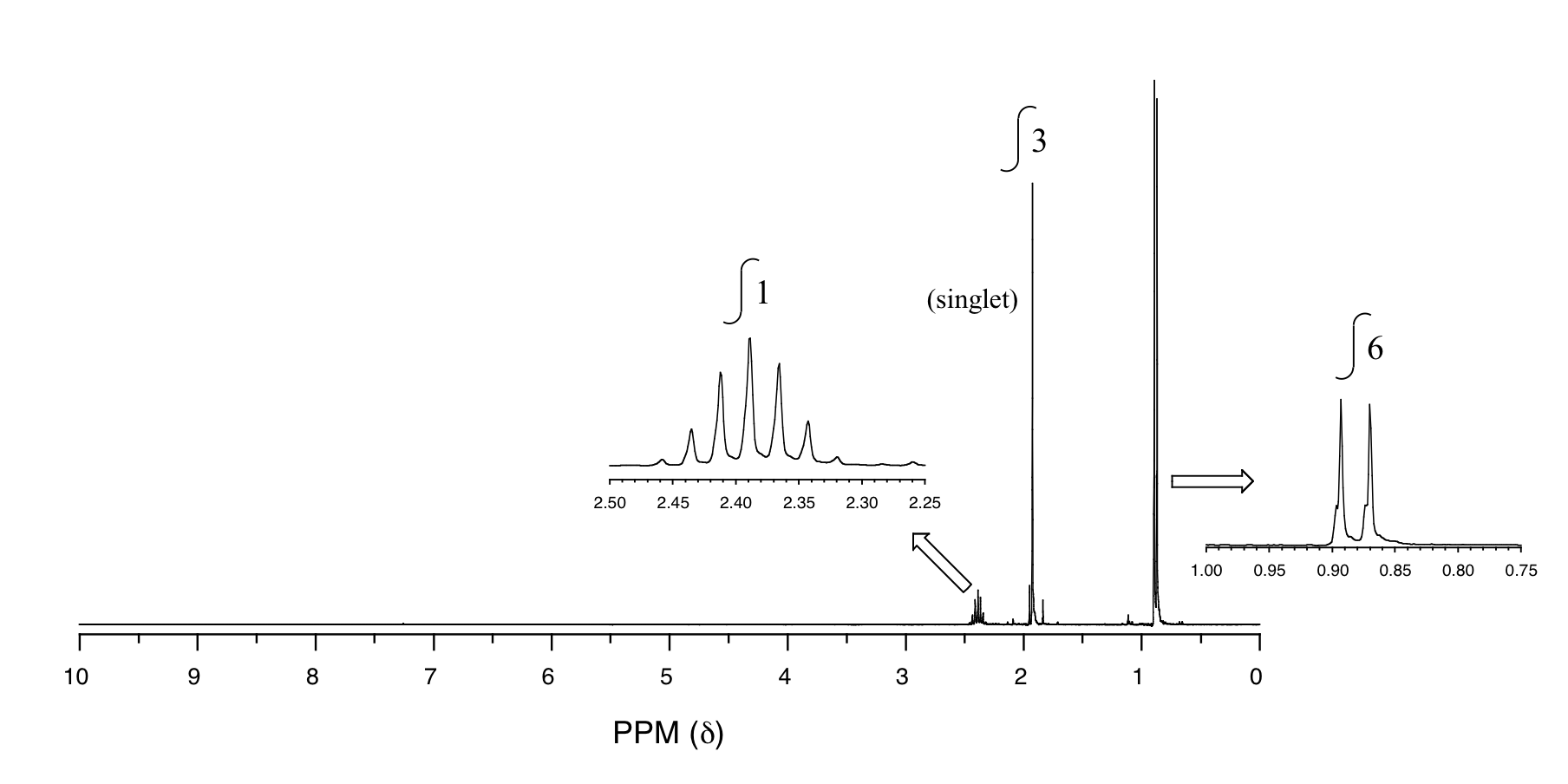
¹³C-NMR:

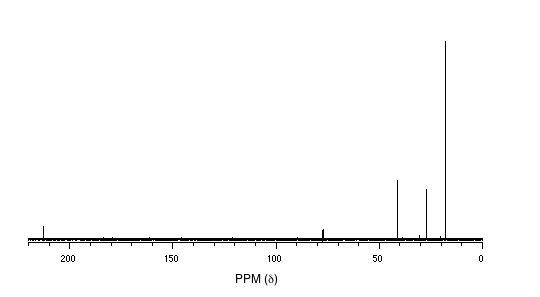
Mass Spectrometry:

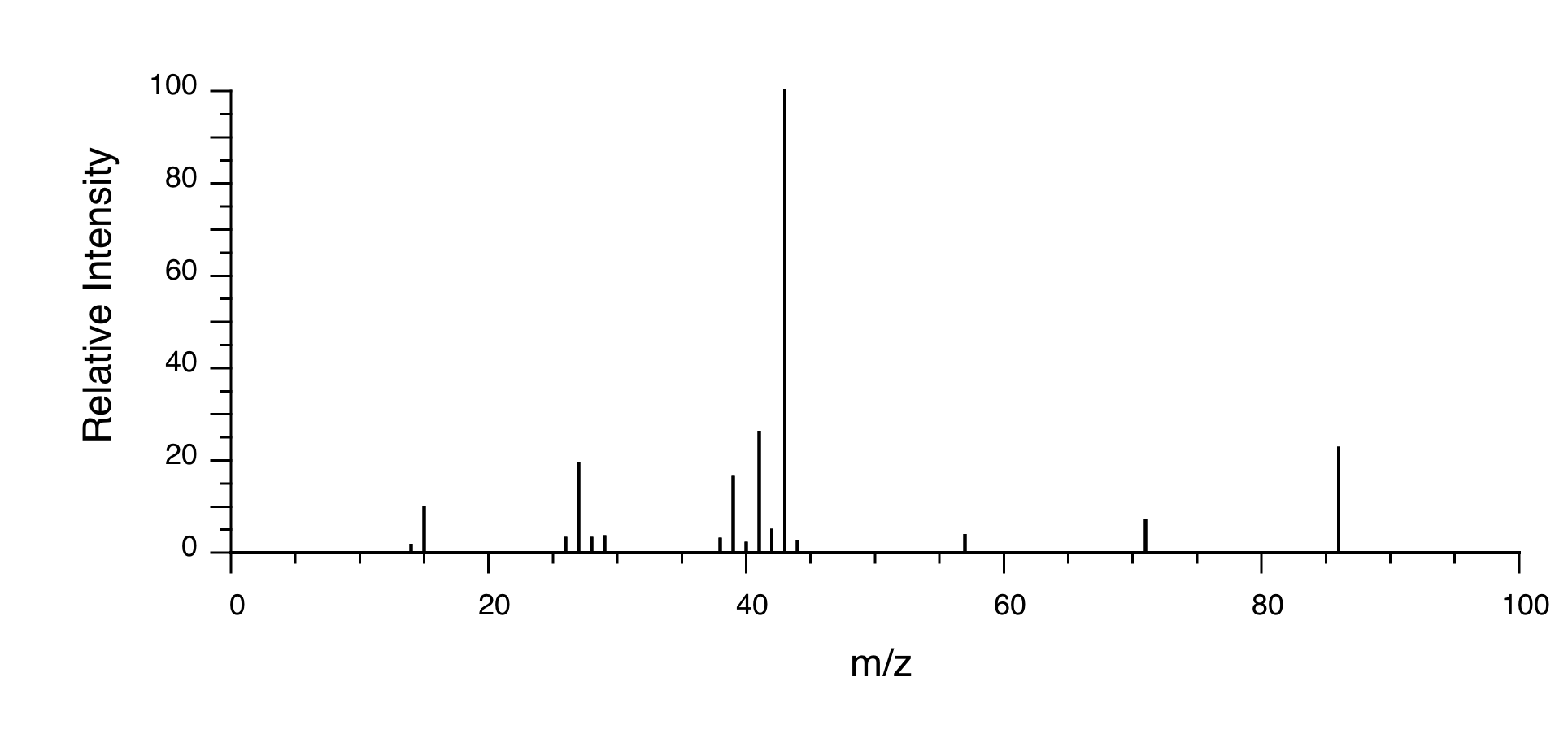
P5.15:You take a ¹H-NMR spectrum of a sample that comes from a bottle of 1-bromopropane. However, you suspect that the bottle might be contaminated with 2-bromopropane. The NMR spectrum shows the following peaks:

δ	splitting	integration
4.3	septet	0.0735
3.4	triplet	0.661
1.9	sextet	0.665
1.7	doublet	0.441
1.0	triplet	1.00

How badly is the bottle contaminated? Specifically, what percent of the molecules in the bottle are 2-bromopropane?

Challenge problems

C5.1: All of the ¹³C-NMR spectra shown in this chapter include a signal due to CDCl₃, the solvent used in each case. Explain the splitting pattern for this signal.

C5.2: Researchers wanted to investigate a reaction which can be catalyzed by the enzyme alcohol dehydrogenase in yeast. They treated 4'-acylpyridine (1) with living yeast, and isolated the alcohol product(s) (some combination of 2A and 2B).

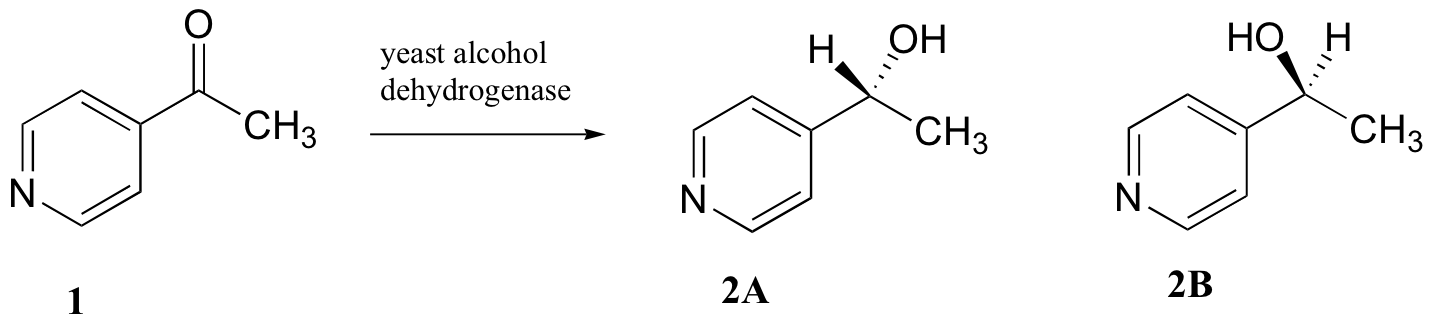
a) Will the products 2A and 2B have identical or different ¹H-NMR spectra? Explain.

b) Suggest a ¹H-NMR experiment that could be used to determine what percent of starting material (1) got turned into product (2A and 2B).

c) With purified 2A/2B, the researchers carried out the subsequent reaction shown below to make 3A and 3B, known as 'Mosher's esters'. Do 3A and 3B have identical or different ¹H-NMR spectra? Explain.

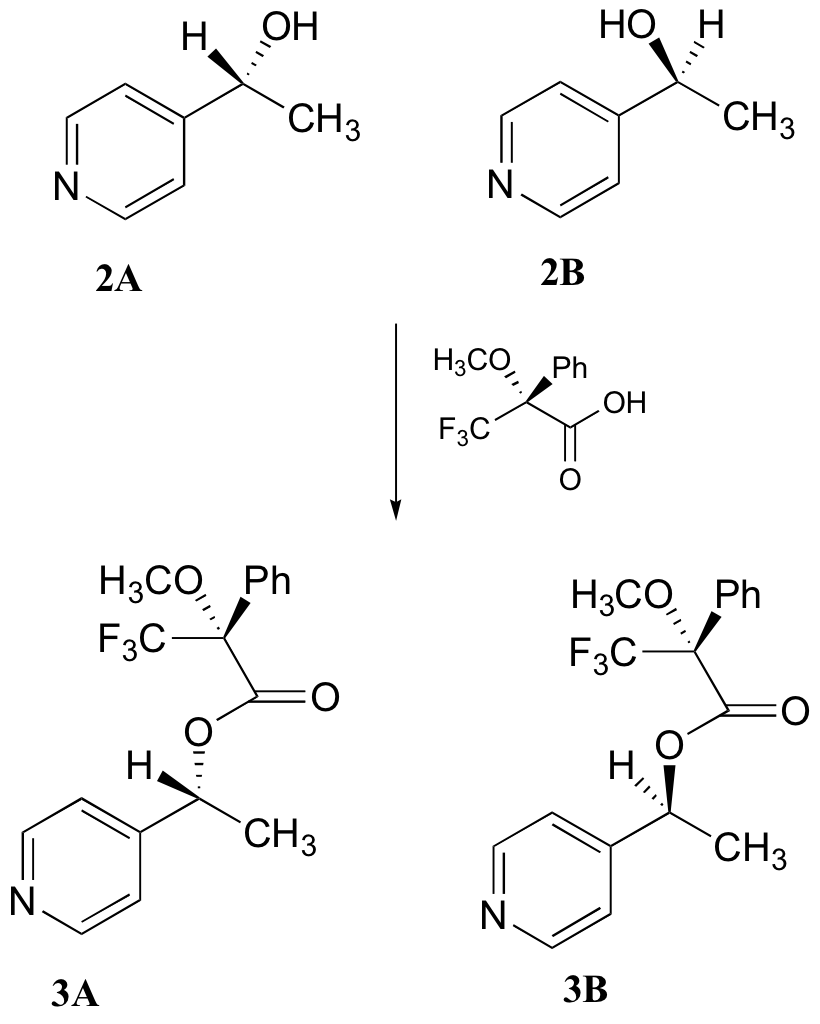
d) Explain, very specifically, how the researchers could use ¹H-NMR to determine the relative amounts of 2A and 2B formed in the reaction catalyzed by yeast enzyme.

Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

Search

Text Color

Text Size

Margin Size

Font Type