15.1: Reaction Rates
- Page ID
- 15137
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- To determine the reaction rate of a reaction.
Reaction rates are usually expressed as the concentration of reactant consumed or the concentration of product formed per unit time. The units are thus moles per liter per unit time, written as M/s, M/min, or M/h. To measure reaction rates, chemists initiate the reaction, measure the concentration of the reactant or product at different times as the reaction progresses, perhaps plot the concentration as a function of time on a graph, and then calculate the change in the concentration per unit time.
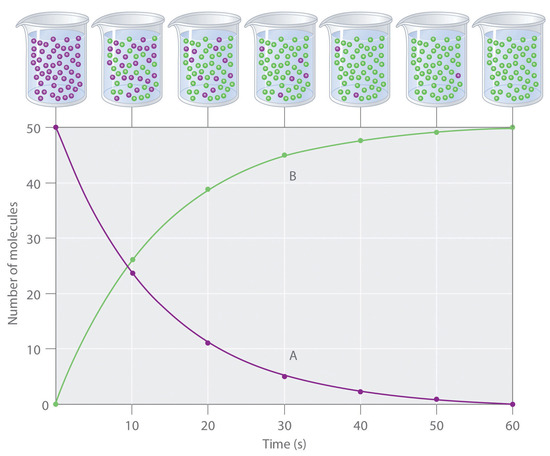
The progress of a simple reaction (A → B) is shown in Figure \(\PageIndex{1}\); the beakers are snapshots of the composition of the solution at 10 s intervals. The number of molecules of reactant (A) and product (B) are plotted as a function of time in the graph. Each point in the graph corresponds to one beaker in Figure \(\PageIndex{1}\). The reaction rate is the change in the concentration of either the reactant or the product over a period of time. The concentration of A decreases with time, while the concentration of B increases with time.
\[\textrm{rate}=\dfrac{\Delta [\textrm B]}{\Delta t}=-\dfrac{\Delta [\textrm A]}{\Delta t} \label{Eq1} \]
Square brackets indicate molar concentrations, and the capital Greek delta (Δ) means “change in.” Because chemists follow the convention of expressing all reaction rates as positive numbers, however, a negative sign is inserted in front of Δ[A]/Δt to convert that expression to a positive number. The reaction rate calculated for the reaction A → B using Equation \(\ref{Eq1}\) is different for each interval (this is not true for every reaction, as shown below). A greater change occurs in [A] and [B] during the first 10 s interval, for example, than during the last, meaning that the reaction rate is greatest at first.
Reaction rates generally decrease with time as reactant concentrations decrease.
A Video Discussing Average Reaction Rates. Video Link: Introduction to Chemical Reaction Kinetics(opens in new window) [youtu.be] (opens in new window)
Determining the Reaction Rate of Hydrolysis of Aspirin
We can use Equation \(\ref{Eq1}\) to determine the reaction rate of hydrolysis of aspirin, probably the most commonly used drug in the world (more than 25,000,000 kg are produced annually worldwide). Aspirin (acetylsalicylic acid) reacts with water (such as water in body fluids) to give salicylic acid and acetic acid, as shown in Figure \(\PageIndex{2}\).
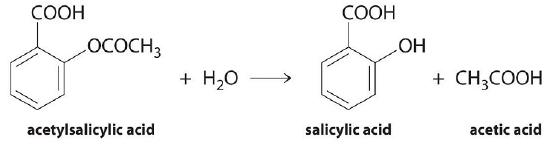
Because salicylic acid is the actual substance that relieves pain and reduces fever and inflammation, a great deal of research has focused on understanding this reaction and the factors that affect its rate. Data for the hydrolysis of a sample of aspirin are in Table \(\PageIndex{1}\) and are shown in the graph in Figure \(\PageIndex{3}\).
| Time (h) | [Aspirin] (M) | [Salicylic Acid] (M) |
|---|---|---|
| *The reaction at pH 7.0 is very slow. It is much faster under acidic conditions, such as those found in the stomach. | ||
| 0 | 5.55 × 10−3 | 0 |
| 2.0 | 5.51 × 10−3 | 0.040 × 10−3 |
| 5.0 | 5.45 × 10−3 | 0.10 × 10−3 |
| 10 | 5.35 × 10−3 | 0.20 × 10−3 |
| 20 | 5.15 × 10−3 | 0.40 × 10−3 |
| 30 | 4.96 × 10−3 | 0.59 × 10−3 |
| 40 | 4.78 × 10−3 | 0.77 × 10−3 |
| 50 | 4.61 × 10−3 | 0.94 × 10−3 |
| 100 | 3.83 × 10−3 | 1.72 × 10−3 |
| 200 | 2.64 × 10−3 | 2.91 × 10−3 |
| 300 | 1.82 × 10−3 | 3.73 × 10−3 |
The data in Table \(\PageIndex{1}\) were obtained by removing samples of the reaction mixture at the indicated times and analyzing them for the concentrations of the reactant (aspirin) and one of the products (salicylic acid).
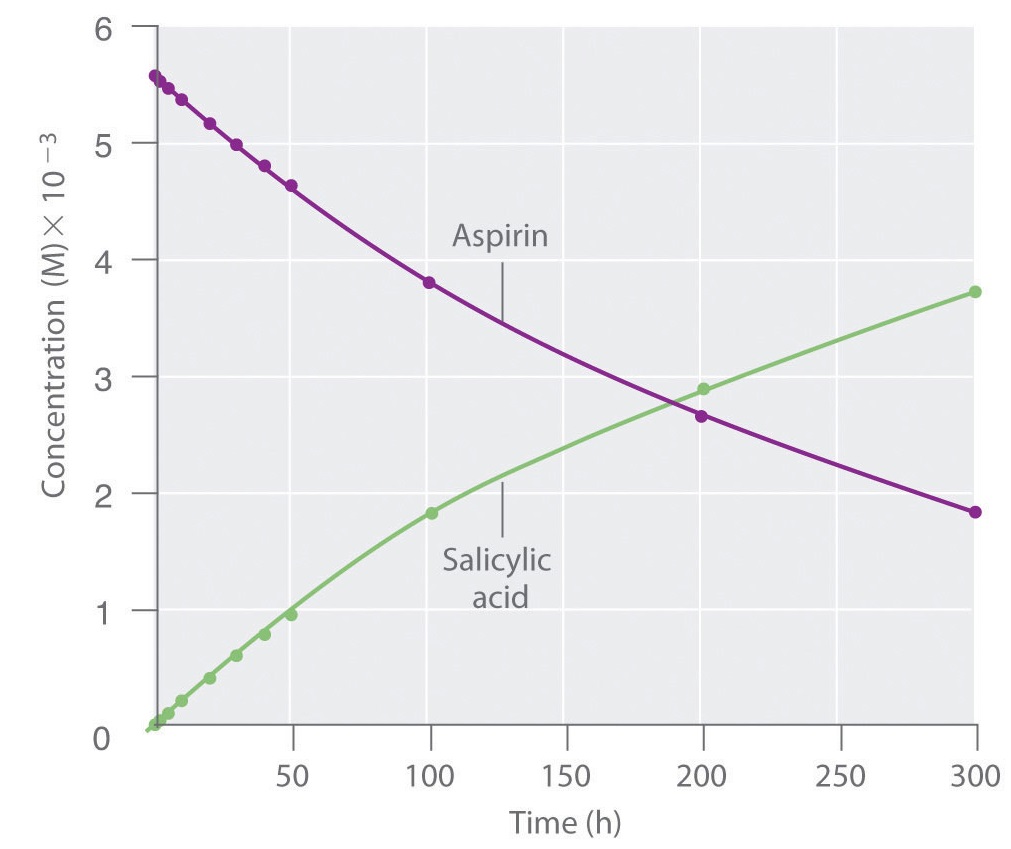
The average reaction rate for a given time interval can be calculated from the concentrations of either the reactant or one of the products at the beginning of the interval (time = t0) and at the end of the interval (t1). Using salicylic acid, the reaction rate for the interval between t = 0 h and t = 2.0 h (recall that change is always calculated as final minus initial) is calculated as follows:
\\&=\frac{0.040\times10^{-3}\textrm{ M}-0\textrm{ M}}{\textrm{2.0 h}}=2.0\times10^{-5}\textrm{ M/h}
\end{align*} \nonumber \]
The reaction rate can also be calculated from the concentrations of aspirin at the beginning and the end of the same interval, remembering to insert a negative sign, because its concentration decreases:
\\&=-\dfrac{(5.51\times10^{-3}\textrm{ M})-(5.55\times10^{-3}\textrm{ M})}{\textrm{2.0 h}}
\\&=2\times10^{-5}\textrm{ M/h}\end{align*} \nonumber \]
If the reaction rate is calculated during the last interval given in Table \(\PageIndex{1}\)(the interval between 200 h and 300 h after the start of the reaction), the reaction rate is significantly slower than it was during the first interval (t = 0–2.0 h):
\\&=-\dfrac{(3.73\times10^{-3}\textrm{ M})-(2.91\times10^{-3}\textrm{ M})}{\textrm{100 h}}
\\&=8.2\times10^{-6}\textrm{ M/h}\end{align*} \nonumber \]
Calculating the Reaction Rate of Fermentation of Sucrose
In the preceding example, the stoichiometric coefficients in the balanced chemical equation are the same for all reactants and products; that is, the reactants and products all have the coefficient 1. Consider a reaction in which the coefficients are not all the same, the fermentation of sucrose to ethanol and carbon dioxide:
\[\underset{\textrm{sucrose}}{\mathrm{C_{12}H_{22}O_{11}(aq)}}+\mathrm{H_2O(l)}\rightarrow\mathrm{4C_2H_5OH(aq)}+4\mathrm{CO_2(g)} \label{Eq2} \]
The coefficients indicate that the reaction produces four molecules of ethanol and four molecules of carbon dioxide for every one molecule of sucrose consumed. As before, the reaction rate can be found from the change in the concentration of any reactant or product. In this particular case, however, a chemist would probably use the concentration of either sucrose or ethanol because gases are usually measured as volumes and, as explained in Chapter 10, the volume of CO2 gas formed depends on the total volume of the solution being studied and the solubility of the gas in the solution, not just the concentration of sucrose. The coefficients in the balanced chemical equation tell us that the reaction rate at which ethanol is formed is always four times faster than the reaction rate at which sucrose is consumed:
\[\dfrac{\Delta[\mathrm{C_2H_5OH}]}{\Delta t}=-\dfrac{4\Delta[\textrm{sucrose}]}{\Delta t} \label{Eq3} \]
The concentration of the reactant—in this case sucrose—decreases with time, so the value of Δ[sucrose] is negative. Consequently, a minus sign is inserted in front of Δ[sucrose] in Equation \(\ref{Eq3}\) so the rate of change of the sucrose concentration is expressed as a positive value. Conversely, the ethanol concentration increases with time, so its rate of change is automatically expressed as a positive value.
Often the reaction rate is expressed in terms of the reactant or product with the smallest coefficient in the balanced chemical equation. The smallest coefficient in the sucrose fermentation reaction (Equation \(\ref{Eq2}\)) corresponds to sucrose, so the reaction rate is generally defined as follows:
\[\textrm{rate}=-\dfrac{\Delta[\textrm{sucrose}]}{\Delta t}=\dfrac{1}{4}\left (\dfrac{\Delta[\mathrm{C_2H_5OH}]}{\Delta t} \right ) \label{Eq4} \]
Consider the thermal decomposition of gaseous N2O5 to NO2 and O2 via the following equation:
Write expressions for the reaction rate in terms of the rates of change in the concentrations of the reactant and each product with time.
Given: balanced chemical equation
Asked for: reaction rate expressions
Strategy:
- Choose the species in the equation that has the smallest coefficient. Then write an expression for the rate of change of that species with time.
- For the remaining species in the equation, use molar ratios to obtain equivalent expressions for the reaction rate.
Solution
A Because O2 has the smallest coefficient in the balanced chemical equation for the reaction, define the reaction rate as the rate of change in the concentration of O2 and write that expression.
B The balanced chemical equation shows that 2 mol of N2O5 must decompose for each 1 mol of O2 produced and that 4 mol of NO2 are produced for every 1 mol of O2 produced. The molar ratios of O2 to N2O5 and to NO2 are thus 1:2 and 1:4, respectively. This means that the rate of change of [N2O5] and [NO2] must be divided by its stoichiometric coefficient to obtain equivalent expressions for the reaction rate. For example, because NO2 is produced at four times the rate of O2, the rate of production of NO2 is divided by 4. The reaction rate expressions are as follows:
\(\textrm{rate}=\dfrac{\Delta[\mathrm O_2]}{\Delta t}=\dfrac{\Delta[\mathrm{NO_2}]}{4\Delta t}=-\dfrac{\Delta[\mathrm{N_2O_5}]}{2\Delta t}\)
The contact process is used in the manufacture of sulfuric acid. A key step in this process is the reaction of \(SO_2\) with \(O_2\) to produce \(SO_3\).
\[2SO_{2(g)} + O_{2(g)} \rightarrow 2SO_{3(g)} \nonumber \]
Write expressions for the reaction rate in terms of the rate of change of the concentration of each species.
- Answer
- \(\textrm{rate}=-\dfrac{\Delta[\mathrm O_2]}{\Delta t}=-\dfrac{\Delta[\mathrm{SO_2}]}{2\Delta t}=\dfrac{\Delta[\mathrm{SO_3}]}{2\Delta t}\)
Instantaneous Rates of Reaction
The instantaneous rate of a reaction is the reaction rate at any given point in time. As the period of time used to calculate an average rate of a reaction becomes shorter and shorter, the average rate approaches the instantaneous rate. Comparing this to calculus, the instantaneous rate of a reaction at a given time corresponds to the slope of a line tangent to the concentration-versus-time curve at that point—that is, the derivative of concentration with respect to time.
The distinction between the instantaneous and average rates of a reaction is similar to the distinction between the actual speed of a car at any given time on a trip and the average speed of the car for the entire trip. Although the car may travel for an extended period at 65 mph on an interstate highway during a long trip, there may be times when it travels only 25 mph in construction zones or 0 mph if you stop for meals or gas. The average speed on the trip may be only 50 mph, whereas the instantaneous speed on the interstate at a given moment may be 65 mph. Whether the car can be stopped in time to avoid an accident depends on its instantaneous speed, not its average speed. There are important differences between the speed of a car during a trip and the speed of a chemical reaction, however. The speed of a car may vary unpredictably over the length of a trip, and the initial part of a trip is often one of the slowest. In a chemical reaction, the initial interval typically has the fastest rate (though this is not always the case), and the reaction rate generally changes smoothly over time.
Chemical kinetics generally focuses on one particular instantaneous rate, which is the initial reaction rate, t = 0. Initial rates are determined by measuring the reaction rate at various times and then extrapolating a plot of rate versus time to t = 0.
Using the reaction shown in Example \(\PageIndex{1}\), calculate the reaction rate from the following data taken at 56°C:
\[2N_2O_{5(g)} \rightarrow 4NO_{2(g)} + O_{2(g)} \nonumber \]
| Time (s) | [N2O5] (M) | [NO2] (M) | [O2] (M) |
|---|---|---|---|
| 240 | 0.0388 | 0.0314 | 0.00792 |
| 600 | 0.0197 | 0.0699 | 0.0175 |
Given: balanced chemical equation and concentrations at specific times
Asked for: reaction rate
Strategy:
- Using the equations in Example \(\PageIndex{1}\), subtract the initial concentration of a species from its final concentration and substitute that value into the equation for that species.
- Substitute the value for the time interval into the equation. Make sure your units are consistent.
Solution
A Calculate the reaction rate in the interval between t1 = 240 s and t2 = 600 s. From Example \(\PageIndex{1}\), the reaction rate can be evaluated using any of three expressions:
Subtracting the initial concentration from the final concentration of N2O5 and inserting the corresponding time interval into the rate expression for N2O5,
B Substituting actual values into the expression,
Similarly, NO2 can be used to calculate the reaction rate:
Allowing for experimental error, this is the same rate obtained using the data for N2O5. The data for O2 can also be used:
Again, this is the same value obtained from the N2O5 and NO2 data. Thus, the reaction rate does not depend on which reactant or product is used to measure it.
Using the data in the following table, calculate the reaction rate of \(SO_2(g)\) with \(O_2(g)\) to give \(SO_3(g)\).
\[2SO_{2(g)} + O_{2(g)} \rightarrow 2SO_{3(g)} \nonumber \]
| Time (s) | [SO2] (M) | [O2] (M) | [SO3] (M) |
|---|---|---|---|
| 300 | 0.0270 | 0.0500 | 0.0072 |
| 720 | 0.0194 | 0.0462 | 0.0148 |
- Answer:
- 9.0 × 10−6 M/s
Summary
In this Module, the quantitative determination of a reaction rate is demonstrated. Reaction rates can be determined over particular time intervals or at a given point in time. A rate law describes the relationship between reactant rates and reactant concentrations. Reaction rates are reported as either the average rate over a period of time or as the instantaneous rate at a single time. Reaction rates can be determined over particular time intervals or at a given point in time.
- General definition of rate for A → B: \[\textrm{rate}=\frac{\Delta [\textrm B]}{\Delta t}=-\frac{\Delta [\textrm A]}{\Delta t} \nonumber \]

