10.26: Osmotic Pressure
- Page ID
- 49680
Suppose we have a solution of sugar in water separated by a membrane from a sample of pure water. The membrane is porous, but the holes are not large enough to allow sucrose molecules to pass through from one side to the other while still being large enough to allow water molecules to pass freely through them. In such a situation, water molecules will be hitting one side of the membrane more often than the other. As a result, water molecules will move more often from right to left through the membrane in the animation than they will in the reverse direction. There will thus be a net flow of water from the compartment containing pure solvent, through the membrane, into the compartment containing the sucrose. This is another example of the tendency for moving molecules to become more thoroughly mixed together. The following movie shows this process, called osmosis.

Osmosis occurs when two solutions of different concentrations are separated by a membrane which will selectively allow some species through it but not others. Then, material flows from the less concentrated to the more concentrated side of the membrane. A membrane which is selective in the way just described is said to be semipermeable. Osmosis is of particular importance in living organisms, since most living tissue is semipermeable in one way or another. In the movie, we have depicted a membrane which is selective purely because of the pore size. In biological systems, the semipermeability relies on a set of solute transporters and channels. The cell membrane is formed of a lipid bilayer with polar head groups facing out, and nonpolar hydrocarbon tails in the middle of the membrane. The consequence is that charged and polar substances cannot cross the membrane. Aquaporins are membrane proteins which allow water, but no other molecule, not even H3O+ to pass through. For other solutes and ions, there exist specific transporters, some which allow a solute to diffuse down a natural gradient, and others which actively pump ions or other solutes in or out of the cell. These transporters, pumps and channels can be gated and regulated as well, allowing a cell to respond to varying osmotic conditions.[1]
A simple demonstration of osmosis is provided by the behavior of red blood cells. If these are immersed in water and observed under the microscope, they will be seen to gradually swell and to finally burst, as seen in the video below. Osmotic flow occurs from the surrounding water into the more concentrated solutions inside the cell. If the blood cells are now immersed in a saturated solution of NaC1, osmosis occurs in the opposite direction, since the solution inside the cell is not as concentrated as that outside. Under the microscope, the blood cells can be seen to shrink and shrivel. In medical practice, any solution which is to be introduced into the blood must take the possibility of osmosis into account. Normal saline, a solution of 0.16 M NaCl (0.16 mol NaCl per dm3 of solution) is always employed for intravenous feeding or injection, because it has the same concentration of salts as blood serum. The video below shows what happens when a red blood cell is immersed in water and osmosis occurs.
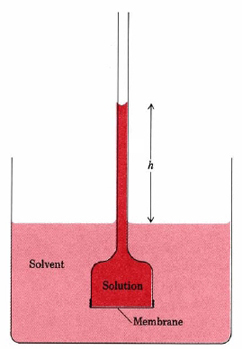
The tendency for osmotic flow to occur from a solvent to a solution is usually measured in terms of what is called the osmotic pressure of the solution, symbol Π. This osmotic pressure is not a pressure which the solution itself exerts but is rather the pressure which must be applied to the solution (but not the solvent) from outside in order to just prevent osmosis from occurring. A simple method for measuring the osmotic pressure is shown in Figure 2. The wider end of a funnel-shaped tube is covered with a membrane. The tube is filled with solution and placed in a container of the solvent. The height of the solution above the solvent increases until a maximum value is reached. The osmotic pressure is then the pressure exerted by the column of a solution of height h where ρ is the density of the solution and g is the gravitational acceleration.
\[\Pi = \rho gh \nonumber \]
Experimentally the osmotic pressure is found to obey a law similar in form to the ideal gas law and hence easy to remember:
\[\Pi V = nRT \label{1} \]
where n is the amount of solute in volume V of solution. In practice it is more useful to have Eq. (1) in terms of the concentration of solute n/V. Accordingly we rearrange it to read
\[\Pi = n * V^{-1}RT \nonumber \] or \[\Pi = cRT \label{2} \]
Equation \(\ref{2}\) is a very useful relationship since it means that we can find the concentration of any solution merely by measuring its osmotic pressure. This, in turn, allows us to find the molar mass of the solute. Suppose we have a solution in which a known mass of solute is dissolved in a known volume of solution. By measuring the osmotic pressure of this solution, we can find the concentration of solute and hence the amount of solute in the total volume. Since we already know the mass of solute, the molar mass follows immediately.
A solution of 20.0 g of polyisobutylene in 1.00 dm3 of benzene was placed in an osmometer, similar to the one shown in Figure 2, at 25°C. After equilibrium had been obtained, the height h was found to be 24.45 mm of benzene. Find the average molar mass of the polymer. The density of the solution is 0.879 g cm–3.
Solution
We must first find the osmotic pressure from the height h with the formula \[\Pi = \rho gh \nonumber \]. In doing this, it is most convenient to convert everything to SI base units.
\[\begin{align} & \Pi =\rho gh=\text{0}\text{.879}\frac{\text{g}}{\text{cm}^{\text{3}}}\text{ }\times \text{ 9}\text{.807}\frac{\text{m}}{\text{s}^{\text{2}}}\text{ }\times \text{ 24}\text{.45 mm} \\ & \text{ }=210.8\frac{\text{g}}{\text{cm}^{\text{3}}}\frac{\text{m}}{\text{s}^{\text{2}}}\text{mm }\times \text{ }\frac{\text{1 kg}}{\text{1000 g}}\text{ }\times \text{ }\left( \frac{\text{100 cm}}{\text{1 m}} \right)^{\text{3}}\text{ }\times \text{ }\frac{\text{1 m}}{\text{1000 mm}} \\ & \text{ }=\text{210}\text{.8}\frac{\text{kg m}^{\text{2}}}{\text{m}^{\text{3}}\text{ s}^{\text{2}}}=\text{210}\text{.8}\frac{\text{kg m}}{\text{s}^{\text{2}}}\text{ }\times \text{ }\frac{\text{1}}{\text{m}^{\text{2}}}=\text{210}\text{.8 N m}^{-\text{2}}=\text{210}\text{.8 Pa} \\ \end{align} \nonumber \]
Knowing Π, we can now calculate the concentration c by rewriting
\[\Pi = cRT \nonumber \]
as
\[\text{c}=\frac{\Pi }{RT}=\frac{\text{210}\text{.8 }\times \text{ 10}^{-\text{3}}\text{ kPa}}{\text{8}\text{.3143 J K}^{-\text{1}}\text{ mol}^{-\text{1}}\text{ }\times \text{ 298}\text{.15 K}}=\text{8}\text{.50 }\times \text{ 10}^{-5}\text{ mol dm}^{-\text{3}} \nonumber \]
For 1 dm3 of solution therefore,
\[n_{solute} = 8.50 × 10^{–5} \text{mol} \nonumber \]
while
\[m_{solute} = 20 \text{g} \nonumber \]
Thus
\[M_{\text{solute}}=\frac{\text{20 g}}{\text{8}\text{.50 }\times \text{ 10}^{-\text{5}}\text{ mol}}\text{2}\text{.35 }\times \text{ 10}^{\text{5}}\text{ g mol}^{-\text{1}} \nonumber \]
Note: An average polyisobutylene molecule thus has a molecular weight of close to a quarter of a million! Such a molecule is made from units, each with a molar mass of 56.10 g mol-1.
An average polyisobutylene chain is thus \[\frac{\text{2}\text{.35 }\times \text{ 10}^{\text{5}}\text{ g mol}^{-\text{1}}}{\text{56}\text{.10 g mol}^{-\text{1}}}=\text{4189} \nonumber \] units long.In other words the chain length is over 8000 carbon atoms in this sample of polymer.
- Nelson, D.L., Cox, M.M. Lehninger Principles of Biochemistry(5th ed.). New York: W.H. Freeman and Company, 2008. pp. 52,389,405.


