2.6: Protons, Neutrons, and Electrons in Atoms
- Page ID
- 369176
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe the locations, charges, and masses of the three main subatomic particles.
- Determine the number of protons and electrons in an atom.
- Write and interpret symbols that depict the atomic number, mass number, and charge of an atom or ion.
- Define the atomic mass unit and average atomic mass
Dalton's Atomic Theory explained a lot about matter, chemicals, and chemical reactions. Nevertheless, it was not entirely accurate, because contrary to what Dalton believed, atoms can, in fact, be broken apart into smaller subunits or subatomic particles. We have been talking about the electron in great detail, but there are two other particles of interest to us: protons and neutrons. We already learned that J. J. Thomson discovered a negatively charged particle, called the electron. Rutherford proposed that these electrons orbit a positive nucleus. In subsequent experiments, he found that there is a smaller positively charged particle in the nucleus, called a proton. There is also a third subatomic particle, known as a neutron.
Electrons
Electrons are one of three main types of particles that make up atoms. Unlike protons and neutrons, which consist of smaller, simpler particles, electrons are fundamental particles that do not consist of smaller particles. They are a type of fundamental particle called leptons. All leptons have an electric charge of \(-1\) or \(0\). Electrons are extremely small. The mass of an electron is only about 1/2000 the mass of a proton or neutron, so electrons contribute virtually nothing to the total mass of an atom. Electrons have an electric charge of \(-1\), which is equal but opposite to the charge of a proton, which is \(+1\). All atoms have the same number of electrons as protons, so the positive and negative charges "cancel out", making atoms electrically neutral.
Unlike protons and neutrons, which are located inside the nucleus at the center of the atom, electrons are found outside the nucleus. Because opposite electric charges attract one another, negative electrons are attracted to the positive nucleus. This force of attraction keeps electrons constantly moving through the otherwise empty space around the nucleus. The figure below is a common way to represent the structure of an atom. It shows the electron as a particle orbiting the nucleus, similar to the way that planets orbit the sun. However, this is an incorrect perspective, as quantum mechanics demonstrates that electrons are more complicated.

Protons
A proton is one of three main particles that make up the atom. Protons are found in the nucleus of the atom. This is a tiny, dense region at the center of the atom. Protons have a positive electrical charge of one \(\left( +1 \right)\) and a mass of 1 atomic mass unit \(\left( \text{amu} \right)\), which is about \(1.67 \times 10^{-27}\) kilograms. Together with neutrons, they make up virtually all of the mass of an atom.
Neutrons
Atoms of all elements—except for most atoms of hydrogen—have neutrons in their nucleus. Unlike protons and electrons, which are electrically charged, neutrons have no charge—they are electrically neutral. That's why the neutrons in the diagram above are labeled \(n^0\). The zero stands for "zero charge". The mass of a neutron is slightly greater than the mass of a proton, which is 1 atomic mass unit \(\left( \text{amu} \right)\). (An atomic mass unit equals about \(1.67 \times 10^{-27}\) kilograms.) A neutron also has about the same diameter as a proton, or \(1.7 \times 10^{-15}\) meters.
As you might have already guessed from its name, the neutron is neutral. In other words, it has no charge whatsoever and is therefore neither attracted to nor repelled from other objects. Neutrons are in every atom (with one exception), and they are bound together with other neutrons and protons in the atomic nucleus.
Before we move on, we must discuss how the different types of subatomic particles interact with each other. When it comes to neutrons, the answer is obvious. Since neutrons are neither attracted to nor repelled from objects, they don't really interact with protons or electrons (beyond being bound into the nucleus with the protons).
Even though electrons, protons, and neutrons are all types of subatomic particles, they are not all the same size. When you compare the masses of electrons, protons, and neutrons, what you find is that electrons have an extremely small mass, compared to either protons or neutrons. On the other hand, the masses of protons and neutrons are fairly similar, although technically, the mass of a neutron is slightly larger than the mass of a proton. Because protons and neutrons are so much more massive than electrons, almost all of the mass of any atom comes from the nucleus, which contains all of the neutrons and protons.
| Particle | Symbol | Mass (amu) | Relative Mass (proton = 1) | Relative Charge | Location |
|---|---|---|---|---|---|
| proton | p+ | 1 | 1 | +1 | inside the nucleus |
| electron | e− | 5.45 × 10−4 | 0.00055 | −1 | outside the nucleus |
| neutron | n0 | 1 | 1 | 0 | inside the nucleus |
Table \(\PageIndex{1}\) gives the properties and locations of electrons, protons, and neutrons. The third column shows the masses of the three subatomic particles in "atomic mass units." An atomic mass unit (\(\text{amu}\)) is defined as one-twelfth of the mass of a carbon-12 atom. Atomic mass units (\(\text{amu}\)) are useful, because, as you can see, the mass of a proton and the mass of a neutron are almost exactly \(1\) in this unit system.
Negative and positive charges of equal magnitude cancel each other out. This means that the negative charge on an electron perfectly balances the positive charge on the proton. In other words, a neutral atom must have exactly one electron for every proton. If a neutral atom has 1 proton, it must have 1 electron. If a neutral atom has 2 protons, it must have 2 electrons. If a neutral atom has 10 protons, it must have 10 electrons. You get the idea. In order to be neutral, an atom must have the same number of electrons and protons.
Atoms—and the protons, neutrons, and electrons that compose them—are extremely small. For example, a carbon atom weighs less than 2 \(\times\) 10−23 g, and an electron has a charge of less than 2 \(\times\) 10−19 C (coulomb). When describing the properties of tiny objects such as atoms, we use appropriately small units of measure, such as the atomic mass unit (amu) and the fundamental unit of charge (e). The amu was originally defined based on hydrogen, the lightest element, then later in terms of oxygen. Since 1961, it has been defined with regard to the most abundant isotope of carbon, atoms of which are assigned masses of exactly 12 amu. (This isotope is known as “carbon-12” as will be discussed later in this module.) Thus, one amu is exactly \(1/12\) of the mass of one carbon-12 atom: 1 amu = 1.6605 \(\times\) 10−24 g. (The Dalton (Da) and the unified atomic mass unit (u) are alternative units that are equivalent to the amu.)
Atomic Number
The number of protons in the nucleus of an atom is its atomic number (\(Z\)). This is the defining trait of an element: Its value determines the identity of the atom. For example, any atom that contains six protons is the element carbon and has the atomic number 6, regardless of how many neutrons or electrons it may have. A neutral atom must contain the same number of positive and negative charges, so the number of protons equals the number of electrons. Therefore, the atomic number also indicates the number of electrons in an atom. The total number of protons and neutrons in an atom is called its mass number (A). The number of neutrons is therefore the difference between the mass number and the atomic number: A – Z = number of neutrons.
\[\begin{align*}
\ce{atomic\: number\:(Z)\: &= \:number\: of\: protons\\
mass\: number\:(A)\: &= \:number\: of\: protons + number\: of\: neutrons\\
A-Z\: &= \:number\: of\: neutrons}
\end{align*} \nonumber \]
Atoms are electrically neutral if they contain the same number of positively charged protons and negatively charged electrons. When the numbers of these subatomic particles are not equal, the atom is electrically charged and is called an ion. The charge of an atom is defined as follows:
Atomic charge = number of protons − number of electrons
As will be discussed in more detail later in this chapter, atoms (and molecules) typically acquire charge by gaining or losing electrons. An atom that gains one or more electrons will exhibit a negative charge and is called an anion. Positively charged atoms called cations are formed when an atom loses one or more electrons. For example, a neutral sodium atom (Z = 11) has 11 electrons. If this atom loses one electron, it will become a cation with a 1+ charge (11 − 10 = 1+). A neutral oxygen atom (Z = 8) has eight electrons, and if it gains two electrons it will become an anion with a 2− charge (8 − 10 = 2−).
Iodine is an essential trace element in our diet; it is needed to produce thyroid hormone. Insufficient iodine in the diet can lead to the development of a goiter, an enlargement of the thyroid gland (Figure \(\PageIndex{2}\)).

The addition of small amounts of iodine to table salt (iodized salt) has essentially eliminated this health concern in the United States, but as much as 40% of the world’s population is still at risk of iodine deficiency. The iodine atoms are added as anions, and each has a 1− charge and a mass number of 127. Determine the numbers of protons, neutrons, and electrons in one of these iodine anions.
Solution
The atomic number of iodine (53) tells us that a neutral iodine atom contains 53 protons in its nucleus and 53 electrons outside its nucleus. Because the sum of the numbers of protons and neutrons equals the mass number, 127, the number of neutrons is 74 (127 − 53 = 74). Since the iodine is added as a 1− anion, the number of electrons is 54 [53 – (1–) = 54].
An ion of platinum has a mass number of 195 and contains 74 electrons. How many protons and neutrons does it contain, and what is its charge?
- Answer
-
78 protons; 117 neutrons; charge is 4+
Chemical Symbols
A chemical symbol is an abbreviation that we use to indicate an element or an atom of an element. For example, the symbol for mercury is Hg (Figure \(\PageIndex{3}\)). We use the same symbol to indicate one atom of mercury (microscopic domain) or to label a container of many atoms of the element mercury (macroscopic domain).

The symbols for several common elements and their atoms are listed in Table \(\PageIndex{2}\). Some symbols are derived from the common name of the element; others are abbreviations of the name in another language. Symbols have one or two letters, for example, H for hydrogen and Cl for chlorine. To avoid confusion with other notations, only the first letter of a symbol is capitalized. For example, Co is the symbol for the element cobalt, but CO is the notation for the compound carbon monoxide, which contains atoms of the elements carbon (C) and oxygen (O). All known elements and their symbols are in the periodic table.
| Element | Symbol | Element | Symbol |
|---|---|---|---|
| aluminum | Al | iron | Fe (from ferrum) |
| bromine | Br | lead | Pb (from plumbum) |
| calcium | Ca | magnesium | Mg |
| carbon | C | mercury | Hg (from hydrargyrum) |
| chlorine | Cl | nitrogen | N |
| chromium | Cr | oxygen | O |
| cobalt | Co | potassium | K (from kalium) |
| copper | Cu (from cuprum) | silicon | Si |
| fluorine | F | silver | Ag (from argentum) |
| gold | Au (from aurum) | sodium | Na (from natrium) |
| helium | He | sulfur | S |
| hydrogen | H | tin | Sn (from stannum) |
| iodine | I | zinc | Zn |
Traditionally, the discoverer (or discoverers) of a new element names the element. However, until the name is recognized by the International Union of Pure and Applied Chemistry (IUPAC), the recommended name of the new element is based on the Latin word(s) for its atomic number. For example, element 106 was called unnilhexium (Unh), element 107 was called unnilseptium (Uns), and element 108 was called unniloctium (Uno) for several years. These elements are now named after scientists or locations; for example, element 106 is now known as seaborgium (Sg) in honor of Glenn Seaborg, a Nobel Prize winner who was active in the discovery of several heavy elements.
Isotopes
The symbol for a specific isotope of any element is written by placing the mass number as a superscript to the left of the element symbol (Figure \(\PageIndex{4}\)). The atomic number is sometimes written as a subscript preceding the symbol, but since this number defines the element’s identity, as does its symbol, it is often omitted. For example, magnesium exists as a mixture of three isotopes, each with an atomic number of 12 and with mass numbers of 24, 25, and 26, respectively. These isotopes can be identified as 24Mg, 25Mg, and 26Mg. These isotope symbols are read as “element, mass number” and can be symbolized consistent with this reading. For instance, 24Mg is read as “magnesium 24,” and can be written as “magnesium-24” or “Mg-24.” 25Mg is read as “magnesium 25,” and can be written as “magnesium-25” or “Mg-25.” All magnesium atoms have 12 protons in their nucleus. They differ only because a 24Mg atom has 12 neutrons in its nucleus, a 25Mg atom has 13 neutrons, and a 26Mg has 14 neutrons.
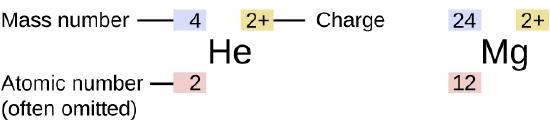
Information about the naturally occurring isotopes of elements with atomic numbers 1 through 10 is given in Table \(\PageIndex{2}\). Note that in addition to standard names and symbols, the isotopes of hydrogen are often referred to using common names and accompanying symbols. Hydrogen-2, symbolized 2H, is also called deuterium and sometimes symbolized D. Hydrogen-3, symbolized 3H, is also called tritium and sometimes symbolized T.
| Element | Symbol | Atomic Number | Number of Protons | Number of Neutrons | Mass (amu) | % Natural Abundance |
|---|---|---|---|---|---|---|
| hydrogen | \(\ce{^1_1H}\) (protium) |
1 | 1 | 0 | 1.0078 | 99.989 |
| \(\ce{^2_1H}\) (deuterium) |
1 | 1 | 1 | 2.0141 | 0.0115 | |
| \(\ce{^3_1H}\) (tritium) |
1 | 1 | 2 | 3.01605 | — (trace) | |
| helium | \(\ce{^3_2He}\) | 2 | 2 | 1 | 3.01603 | 0.00013 |
| \(\ce{^4_2He}\) | 2 | 2 | 2 | 4.0026 | 100 | |
| lithium | \(\ce{^6_3Li}\) | 3 | 3 | 3 | 6.0151 | 7.59 |
| \(\ce{^7_3Li}\) | 3 | 3 | 4 | 7.0160 | 92.41 | |
| beryllium | \(\ce{^9_4Be}\) | 4 | 4 | 5 | 9.0122 | 100 |
| boron | \(\ce{^{10}_5B}\) | 5 | 5 | 5 | 10.0129 | 19.9 |
| \(\ce{^{11}_5B}\) | 5 | 5 | 6 | 11.0093 | 80.1 | |
| carbon | \(\ce{^{12}_6C}\) | 6 | 6 | 6 | 12.0000 | 98.89 |
| \(\ce{^{13}_6C}\) | 6 | 6 | 7 | 13.0034 | 1.11 | |
| \(\ce{^{14}_6C}\) | 6 | 6 | 8 | 14.0032 | — (trace) | |
| nitrogen | \(\ce{^{14}_7N}\) | 7 | 7 | 7 | 14.0031 | 99.63 |
| \(\ce{^{15}_7N}\) | 7 | 7 | 8 | 15.0001 | 0.37 | |
| oxygen | \(\ce{^{16}_8O}\) | 8 | 8 | 8 | 15.9949 | 99.757 |
| \(\ce{^{17}_8O}\) | 8 | 8 | 9 | 16.9991 | 0.038 | |
| \(\ce{^{18}_8O}\) | 8 | 8 | 10 | 17.9992 | 0.205 | |
| fluorine | \(\ce{^{19}_9F}\) | 9 | 9 | 10 | 18.9984 | 100 |
| neon | \(\ce{^{20}_{10}Ne}\) | 10 | 10 | 10 | 19.9924 | 90.48 |
| \(\ce{^{21}_{10}Ne}\) | 10 | 10 | 11 | 20.9938 | 0.27 | |
| \(\ce{^{22}_{10}Ne}\) | 10 | 10 | 12 | 21.9914 | 9.25 |
Atomic Mass
Because each proton and each neutron contribute approximately one amu to the mass of an atom, and each electron contributes far less, the atomic mass of a single atom is approximately equal to its mass number (a whole number). However, the average masses of atoms of most elements are not whole numbers because most elements exist naturally as mixtures of two or more isotopes.
The mass of an element shown in a periodic table or listed in a table of atomic masses is a weighted, average mass of all the isotopes present in a naturally occurring sample of that element. This is equal to the sum of each individual isotope’s mass multiplied by its fractional abundance.
\[\mathrm{average\: mass}=\sum_{i}(\mathrm{fractional\: abundance\times isotopic\: mass})_i \nonumber \]
For example, the element boron is composed of two isotopes: About 19.9% of all boron atoms are 10B with a mass of 10.0129 amu, and the remaining 80.1% are 11B with a mass of 11.0093 amu. The average atomic mass for boron is calculated to be:
\[\begin{align*}
\textrm{boron average mass} &=\mathrm{(0.199\times10.0129\: amu)+(0.801\times11.0093\: amu)}\\
&=\mathrm{1.99\: amu+8.82\: amu}\\
&=\mathrm{10.81\: amu}
\end{align*} \nonumber \]
It is important to understand that no single boron atom weighs exactly 10.8 amu; 10.8 amu is the average mass of all boron atoms, and individual boron atoms weigh either approximately 10 amu or 11 amu.
A meteorite found in central Indiana contains traces of the noble gas neon picked up from the solar wind during the meteorite’s trip through the solar system. Analysis of a sample of the gas showed that it consisted of 91.84% 20Ne (mass 19.9924 amu), 0.47% 21Ne (mass 20.9940 amu), and 7.69% 22Ne (mass 21.9914 amu). What is the average mass of the neon in the solar wind?
Solution
\[\begin{align*}
\mathrm{average\: mass} &=\mathrm{(0.9184\times19.9924\: amu)+(0.0047\times20.9940\: amu)+(0.0769\times21.9914\: amu)}\\
&=\mathrm{(18.36+0.099+1.69)\:amu}\\
&=\mathrm{20.15\: amu}
\end{align*} \nonumber \]
The average mass of a neon atom in the solar wind is 20.15 amu. (The average mass of a terrestrial neon atom is 20.1796 amu. This result demonstrates that we may find slight differences in the natural abundance of isotopes, depending on their origin.)
A sample of magnesium is found to contain 78.70% of 24Mg atoms (mass 23.98 amu), 10.13% of 25Mg atoms (mass 24.99 amu), and 11.17% of 26Mg atoms (mass 25.98 amu). Calculate the average mass of a Mg atom.
- Answer
-
24.31 amu
We can also do variations of this type of calculation, as shown in the next example.
Naturally occurring chlorine consists of 35Cl (mass 34.96885 amu) and 37Cl (mass 36.96590 amu), with an average mass of 35.453 amu. What is the percent composition of Cl in terms of these two isotopes?
Solution
The average mass of chlorine is the fraction that is 35Cl times the mass of 35Cl plus the fraction that is 37Cl times the mass of 37Cl.
\[\mathrm{average\: mass=(fraction\: of\: ^{35}Cl\times mass\: of\: ^{35}Cl)+(fraction\: of\: ^{37}Cl\times mass\: of\: ^{37}Cl)} \nonumber \]
If we let x represent the fraction that is 35Cl, then the fraction that is 37Cl is represented by 1.00 − x.
(The fraction that is 35Cl + the fraction that is 37Cl must add up to 1, so the fraction of 37Cl must equal 1.00 − the fraction of 35Cl.)
Substituting this into the average mass equation, we have:
\[\begin{align*}
\mathrm{35.453\: amu} &=(x\times 34.96885\: \ce{amu})+[(1.00-x)\times 36.96590\: \ce{amu}]\\
35.453 &=34.96885x+36.96590-36.96590x\\
1.99705x &=1.513\\
x&=\dfrac{1.513}{1.99705}=0.7576
\end{align*} \nonumber \]
So solving yields: x = 0.7576, which means that 1.00 − 0.7576 = 0.2424. Therefore, chlorine consists of 75.76% 35Cl and 24.24% 37Cl.
Naturally occurring copper consists of 63Cu (mass 62.9296 amu) and 65Cu (mass 64.9278 amu), with an average mass of 63.546 amu. What is the percent composition of Cu in terms of these two isotopes?
- Answer
-
69.15% Cu-63 and 30.85% Cu-65
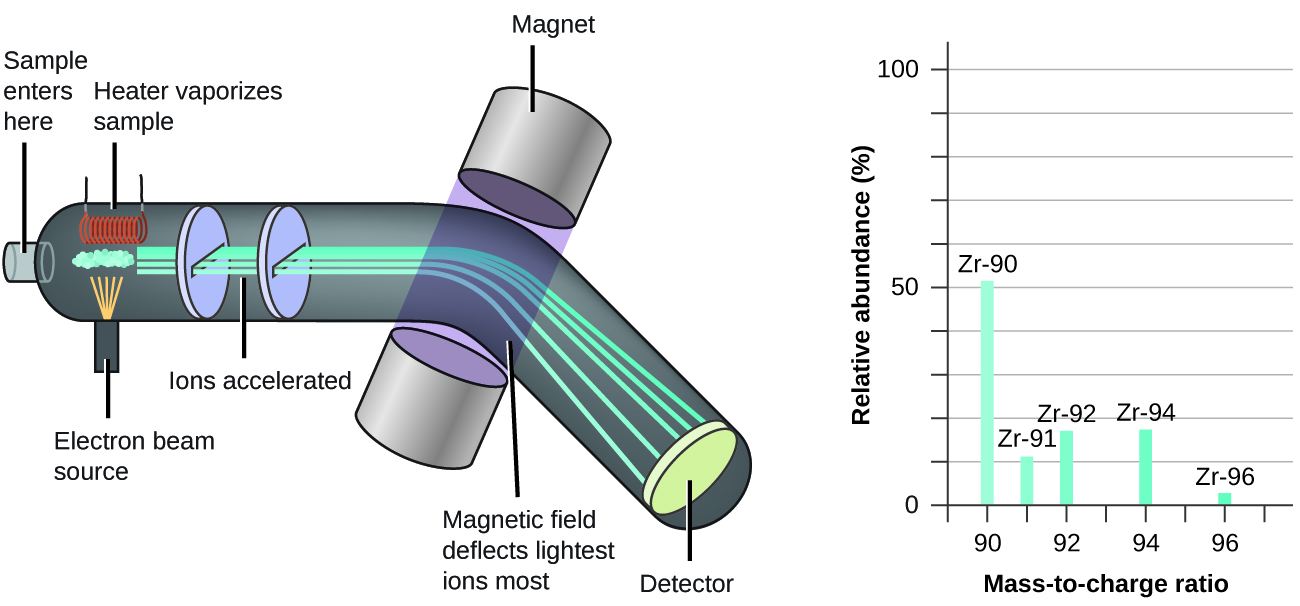
The occurrence and natural abundances of isotopes can be experimentally determined using an instrument called a mass spectrometer. Mass spectrometry (MS) is widely used in chemistry, forensics, medicine, environmental science, and many other fields to analyze and help identify the substances in a sample of material. In a typical mass spectrometer (Figure \(\PageIndex{5}\)), the sample is vaporized and exposed to a high-energy electron beam that causes the sample’s atoms (or molecules) to become electrically charged, typically by losing one or more electrons. These cations then pass through a (variable) electric or magnetic field that deflects each cation’s path to an extent that depends on both its mass and charge (similar to how the path of a large steel ball bearing rolling past a magnet is deflected to a lesser extent that that of a small steel BB). The ions are detected, and a plot of the relative number of ions generated versus their mass-to-charge ratios (a mass spectrum) is made. The height of each vertical feature or peak in a mass spectrum is proportional to the fraction of cations with the specified mass-to-charge ratio. Since its initial use during the development of modern atomic theory, MS has evolved to become a powerful tool for chemical analysis in a wide range of applications.
Video \(\PageIndex{1}\): Watch this video from the Royal Society for Chemistry for a brief description of the rudiments of mass spectrometry.
Summary
An atom consists of a small, positively charged nucleus surrounded by electrons. The nucleus contains protons and neutrons; its diameter is about 100,000 times smaller than that of the atom. The mass of one atom is usually expressed in atomic mass units (amu), which is referred to as the atomic mass. An amu is defined as exactly \(1/12\) of the mass of a carbon-12 atom and is equal to 1.6605 \(\times\) 10−24 g.
Protons are relatively heavy particles with a charge of 1+ and a mass of 1.0073 amu. Neutrons are relatively heavy particles with no charge and a mass of 1.0087 amu. Electrons are light particles with a charge of 1− and a mass of 0.00055 amu. The number of protons in the nucleus is called the atomic number (Z) and is the property that defines an atom’s elemental identity. The sum of the numbers of protons and neutrons in the nucleus is called the mass number and, expressed in amu, is approximately equal to the mass of the atom. An atom is neutral when it contains equal numbers of electrons and protons.
Isotopes of an element are atoms with the same atomic number but different mass numbers; isotopes of an element, therefore, differ from each other only in the number of neutrons within the nucleus. When a naturally occurring element is composed of several isotopes, the atomic mass of the element represents the average of the masses of the isotopes involved. A chemical symbol identifies the atoms in a substance using symbols, which are one-, two-, or three-letter abbreviations for the atoms.
Key Equations
- \(\mathrm{average\: mass}=\sum_{i}(\mathrm{fractional\: abundance \times isotopic\: mass})_i\)
Glossary
- anion
- negatively charged atom or molecule (contains more electrons than protons)
- atomic mass
- average mass of atoms of an element, expressed in amu
- atomic mass unit (amu)
- (also, unified atomic mass unit, u, or Dalton, Da) unit of mass equal to \(\dfrac{1}{12}\) of the mass of a 12C atom
- atomic number (Z)
- number of protons in the nucleus of an atom
- cation
- positively charged atom or molecule (contains fewer electrons than protons)
- chemical symbol
- one-, two-, or three-letter abbreviation used to represent an element or its atoms
- Dalton (Da)
- alternative unit equivalent to the atomic mass unit
- fundamental unit of charge
- (also called the elementary charge) equals the magnitude of the charge of an electron (e) with e = 1.602 \(\times\) 10−19 C
- ion
- electrically charged atom or molecule (contains unequal numbers of protons and electrons)
- mass number (A)
- sum of the numbers of neutrons and protons in the nucleus of an atom
- unified atomic mass unit (u)
- alternative unit equivalent to the atomic mass unit

