15.6: Ferro-, Ferri- and Antiferromagnetism

The magnetism of metals and other materials are determined by the orbital and spin motions of the unpaired electrons and the way in which unpaired electrons align with each other. All magnetic substances are paramagnetic at sufficiently high temperature, where the thermal energy (kT) exceeds the interaction energy between spins on neighboring atoms. Below a certain critical temperature, spins can adopt different kinds of ordered arrangements.

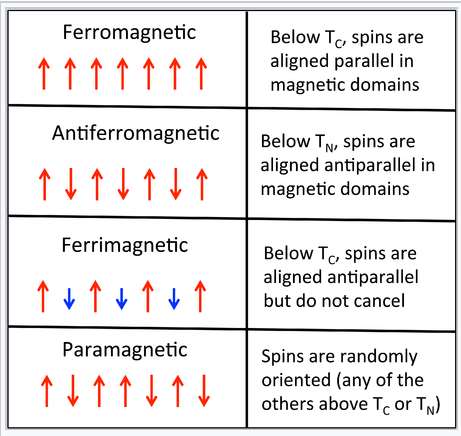
A pictorial description of the ordering of spins in ferromagnetism, antiferromagnetism, ferrimagnetism, and paramagnetism

Let's begin by considering an individual atom in the bcc structure of iron metal. Fe is in group VIIIb of the periodic table, so it has eight valence electrons. The atom is promoted to the 4s¹3d⁷ state in order to make bonds. A localized picture of the d-electrons for an individual iron atom might look like this:

Since each unpaired electron has a spin moment of 1/2, the total spin angular momentum, S, for this atom is:

\(S = 3\frac{1}{2} = \frac{3}{2}\) (in units of h/2π)

We can think of each Fe atom in the solid as a little bar magnet with a spin-only moment S of 3/2. The spin moments of neigboring atoms can align in parallel (↑ ↑), antiparallel (↑ ↓), or random fashion. In bcc Fe, the tendency is to align parallel because of the positive sign of the exchange interaction. This results in ferromagnetic ordering, in which all the spins within a magnetic domain (typically hundreds of unit cells in width) have the same orientation, as shown in the figure at the right. Conversely, a negative exchange interaction between neighboring atoms in bcc Cr results in antiferromagnetic ordering. A third arrangement, ferrimagnetic ordering, results from an antiparallel alignment of spins on neighboring atoms when the magnetic moments of the neighbors are unequal. In this case, the spin moments do not cancel and there is a net magnetization. The ordering mechanism is like that of an antiferromagnetic solid, but the magnetic properties resemble those of a ferromagnet. Ferrimagnetic ordering is most common in metal oxides, as we will learn in Chapter 7.

Magnetization and susceptibility

The magnetic susceptibility, χ, of a solid depends on the ordering of spins. Paramagnetic, ferromagnetic, antiferromagnetic, and ferrimagnetic solids all have χ > 0, but the magnitude of their susceptibility varies with the kind of ordering and with temperature. We will see these kinds of magnetic ordering primarily among the 3d and 4f elements and their alloys and compounds. For example, Fe, Co, Ni, Nd₂Fe₁₄B, SmCo₅, and YCo₅ are all ferromagnets, Cr and MnO are antiferromagnets, and Fe₃O₄ and CoFe₂O₄ are ferrimagnets. Diamagnetic compounds have a weak negative susceptibility (χ < 0).

Definitions

• H = applied magnetic field (units: Henry (H))
• B = induced magnetic field in a material (units: Tesla (T))
• M = magnetization, which represents the magnetic moments within a material in the presence of an external field H.

Magnetic susceptibility χ = M/H

Usually, χ is given in molar units in the cgs system:

χ_M = molar susceptibility (units: cm³/mol)

Typical values of χ_M:

Compound	Type of Magnetism	χ at 300K (cm^3/mol)
SiO2	Diamagnetic	- 3 x 10^-4
Pt metal	Pauli paramagnetic	+ 2 x 10^-4
Gd2(SO4)3^.8H2O	Paramagnetic	+ 5 x 10^-2
Ni-Fe alloy	Ferromagnetic	+ 10^4 - 10^6

To correlate χ with the number of unpaired electrons in a compound, we first correct for the small diamagnetic contribution of the core electrons:

\[\chi^{corr} = \chi^{obs}- \chi^{diamagnetic\: cores}\]

Susceptibility of paramagnets

For a paramagnetic substance,

\[\chi^{corr}_{M} = \frac{C}{T}\]

The inverse relationship between the magnetic susceptibility and T, the absolute temperature, is called Curie's Law, and the proportionality constant C is the Curie constant:

\[C= \frac{N_{A}}{3k_{B}}\mu^{2}_{eff}\]

Note that C is not a "constant" in the usual sense, because it depends on µ_eff, the effective magnetic moment of the molecule or ion, which in turn depends on its number of unpaired electrons:

\[\mu_{eff} = \sqrt{n(n+2)}\mu_{B}\]

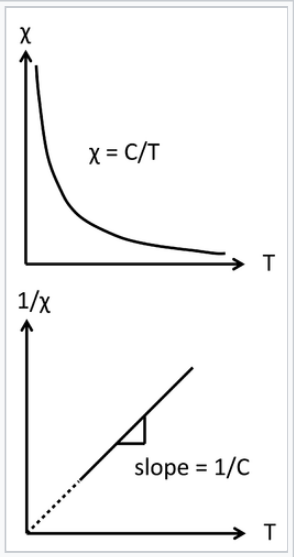
Curie law behavior of a paramagnet. A plot of 1/χ vs. absolute temperature is a straight line, with a slope of 1/C and an intercept of zero.

Here µ_B is the Bohr magneton, a physical constant defined as µ_B = eh/4πm_e = 9.274 x 10^-21 erg/gauss (in cgs units).

In cgs units, we can combine physical constants,

\[\frac{N_{A}}{3k_{B}} \mu^{2}_{B} = .125\]

Combining these equations, we obtain

\[\chi^{corr}_{M} = \frac{.125}{T}(\frac{\mu_{eff}}{\mu_{B}})^{2}\]

These equations relate the molar susceptibility, a bulk quantity that can be measured with a magnetometer, to µ_eff, a quantity that can be calculated from the number of unpaired electrons, n. Two important points to note about this formula are:

• The magnetic susceptibility is inversely proportional to the absolute temperature, with a proportionality constant C (Curie's Law)
• So far we are talking only about paramagnetic substances, where there is no interaction between neighboring atoms.

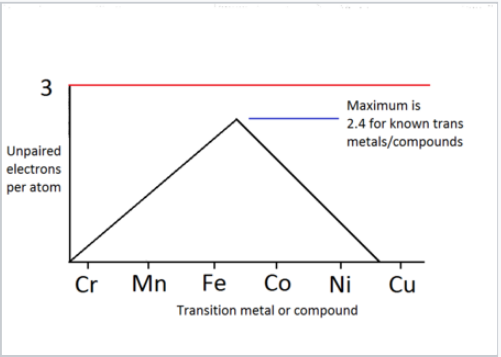
Number of unpaired electrons per atom, determined from Curie constants of transition metals and their 1:1 alloys.

Returning to the isolated Fe atom with its three unpaired electrons, we can measure the Curie constant for iron metal (above the temperature of its transition to a paramagnetic solid) and compare it to the calculation of µ_eff. Since n = 3, we calculate:

\[\mu_{eff}= \sqrt{(3)(5)} \mu_{B} = 3.87\mu_{B}\]

The plot at the right shows the number of unpaired electrons per atom, calculated from measured Curie constants, for the magnetic elements and 1:1 alloys in the 3d series. The plot peaks at a value of 2.4 spins per atom, slightly lower than we calculated for an isolated iron atom. This reflects that fact that there is some pairing of d-electrons, i.e., that they do contribute somewhat to bonding in this part of the periodic table.

Susceptibility of ferro-, ferri-, and antiferromagnets

Below a certain critical temperature, the spins of a solid paramagnetic substance order and the susceptibility deviates from simple Curie-law behavior. Because the ordering depends on the short-range exchange interaction, this critical temperature varies widely. Metals and alloys in the 3d series tend to have high critical temperatures because the atoms are directly bonded to each other and the interaction is strong. For example, Fe and Co have critical temperatures (also called the Curie temperature, T_c, for ferromagnetic substances) of 1043 and 1400 K, respectively. The Curie temperature is determined by the strength of the magnetic exchange interaction and by the number of unpaired electrons per atom. The number of unpaired electrons peaks between Fe and Co as the d-band is filled, and the exchange interaction is stronger for Co than for Fe. In contrast to ferromagnetic metals and alloys, paramagnetic salts of transition metal ions typically have critical temperatures below 1K because the magnetic ions are not directly bonded to each other and thus their spins are very weakly coupled in the solid state. For example, in gadolinium sulfate, the paramagnetic Gd³⁺ ions are isolated from each other by SO₄^2- ions.

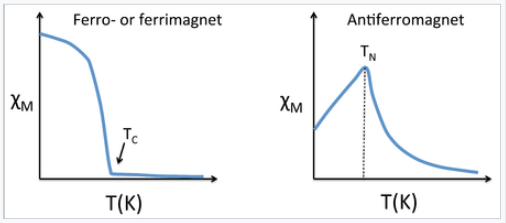
Magnetic susceptibility vs temperature (Kelvin) for ferrimagnetic, ferromagnetic, and antiferromagnetic materials

Above the critical temperature T_C, ferromagnetic compounds become paramagnetic and obey the Curie-Weiss law:

\[\chi= \frac{C}{T-T_{c}}\]

This is similar to the Curie law, except that the plot of 1/χ vs. T is shifted to a positive intercept T_C on the temperature axis. This reflects the fact that ferromagnetic materials (in their paramagnetic state) have a greater tendency for their spins to align in a magnetic field than an ordinary paramagnet in which the spins do not interact with each other. Ferrimagnets follow the same kind of ordering behavior. Typical plots of χ vs. T and 1/χ vs. T for ferro-/ferrimagnets are shown above and below.

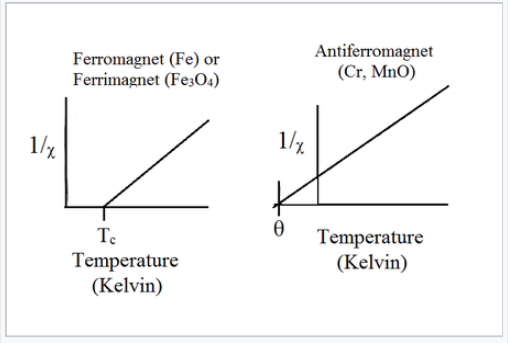
Plots of 1/χ vs. T for ferromagnets, ferrimagnets, and antiferromagnets.

Antiferromagnetic solids are also paramagnetic above a critical temperature, which is called the Néel temperature, T_N. For antiferromagnets, χ reaches a maximum at T_N and is smaller at higher temperature (where the paramagnetic spins are further disordered by thermal energy) and at lower temperature (where the spins pair up). Typically, antiferromagnets retain some positive susceptibility even at very low temperature because of canting of their paired spins. However the maximum value of χ is much lower for an antiferromagnet than it is for a ferro- or ferrimagnet. The Curie-Weiss law is also modified for an antiferromagnet, reflecting the tendency of spins (in the paramagnetic state above T_N) to resist parallel ordering. A plot of 1/χ vs. T intercepts the temperature axis at a negative temperature, -θ, and the Curie-Weiss law becomes:

\[\chi= \frac{C}{T + \theta}\]

Ordering of spins below T_C

Below T_C, the spins align spontaneously in ferro- and ferrimagnets. Complex magnetization behavior is observed that depends on the history of the sample. For example, if a ferromagnetic material is cooled in the absence of an applied magnetic field, it forms a mosaic structure of magnetic domains that each have internally aligned spins. However, neighboring domains tend to align the opposite way in order to minimize the total energy of the system. This is illustrated in the figure at the left for a Nd-Fe-B magnet. The sample consists of 5-10 µm wide crystal grains that can be easily distinguished by the sharp boundaries in the image. Within each grain are a series of lighter and darker stripes (imaged by using the optical Kerr effect) that are ferromagnetic domains with opposite orientations. Averaged over the whole sample, these domains have random orientation so the net magnetization is zero.

Microcrystalline grains within a piece of Nd2Fe14B (the alloy used in neodymium magnets) with magnetic domains made visible with a Kerr microscope. The domains are the light and dark stripes visible within each grain.

When a sample like this one is magnetized (i.e., exposed to a strong magnetic field), the domain walls move and the favorably aligned domains grow at the expense of those with the opposite orientation. This transformation can be seen in real time in the Kerr microscope. The domain walls are typically hundreds of atoms wide, so movement of a domain wall involves a cooperative tilting of spin orientation (analogous to "the wave" in a sports stadium) and is a relatively low energy process.

The movement of domain walls in a grain of silicon steel is driven in this movie by increasing the external magnetic field in the "downward" direction, and is imaged using a Kerr microscope. White areas are domains with their magnetization directed up, dark areas - which eventually comprise the entire grain - are domains with their magnetization directed down.

The process of magnetization moves the solid away from its lowest energy state (random domain orientation), so magnetization involves input of energy. When the external magnetic field is removed, the domain walls relax somewhat, but the solid (especially in the case of a "hard" magnet) can retain much of its magnetization. If you have ever magnetized a nail or a paper clip by using a permanent magnet, what you were doing was moving the walls of the magnetic domains inside the ferromagnet. The object thereafter retains the "memory" of its magnetization. However, annealing a permanent magnet destroys the magnetization by returning the system to its lowest energy state in which all the magnetic domains cancel each other.

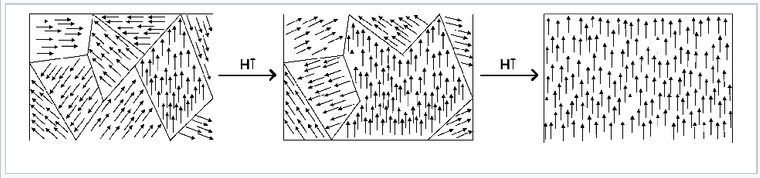
Rotation of orientation and increase in size of magnetic domains in response to an externally applied magnetic field.

Magnetic hysteresis. Cycling a ferro- or ferrimagnetic material in a magnetic field results in hysteresis in the magnetization of the material, as shown in the figure at the left. At the beginning, the magnetization is zero, but it begins to rise rapidly as the magnetic field is applied. At high field, the magnetic domains are aligned and the magnetization is said to be saturated. When the field is removed, a certain remanent magnetization (indicated as the point B_r on the graph) is retained, i.e., the material is magnetized. Applying a field in the opposite direction begins to orient the magnetic domains in the other direction, and at a field H_c (the coercive field), the magnetization of the sample is reduced to zero. Eventually the material reaches saturation in the opposite direction, and when the field is removed again, it has remanent magnetization Br, but in the opposite direction. As the field continues to reverse, the magnet follows the hysteresis loop as indicated by the arrows. The area of colored region inside the loop is proportional to the magnetic work done in each cycle. When the field cycles rapidly (for example, in the core of a transformer, or in read-write cycles of a magnetic disk) this work is turned into heat.

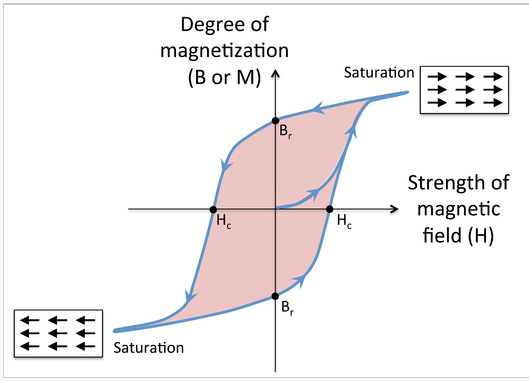
Magnetization of a ferro- or ferrimagnet vs. applied magnetic field H. Starting at the origin, the upward curve is the initial magnetization curve. The downward curve after saturation, along with the lower return curve, form the main loop. The intercepts Hc and Br are the coercivity and remanent magnetization.