7.1: Chirality and stereoisomers

We turn now to concept of chirality that formed the basis of the story about Louis Pasteur in the beginning of this chapter. Recall that the term chiral, from the Greek work for 'hand', refers to anything which cannot be superimposed on its own mirror image. Your hands, of course, are chiral - you cannot superimpose your left hand on your right, and you cannot fit your left hand into a right-handed glove (which is also a chiral object). Another way of saying this is that your hands do not have a mirror plane of symmetry: you cannot find any plane which bisects your hand in such a way that one side of the plane is a mirror image of the other side. Chiral objects do not have a plane of symmetry.

Your face, on the other hand is achiral - lacking chirality - because, some small deviations notwithstanding, you could superimpose your face onto its mirror image. If someone were to show you a mirror image photograph of your face, you could line the image up, point-for-point, with your actual face. Your face has a plane of symmetry, because the left side is the mirror image of the right side.

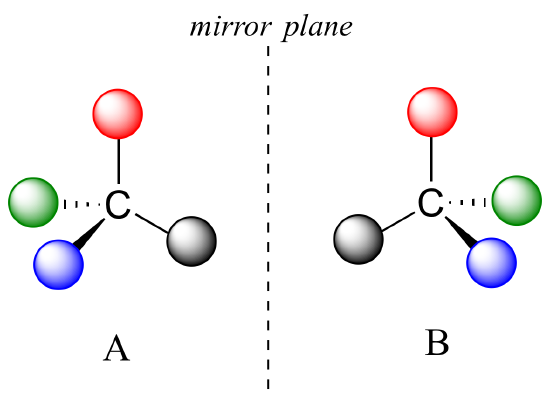
What Pasteur, Biot, and their contemporaries did not yet fully understand when Pasteur made his discovery of molecular chirality was the source of chirality at the molecular level. It stood to reason that a chiral molecule is one that does not contain a plane of symmetry, and thus cannot be superimposed on its mirror image. We now know that chiral molecules contain one or more chiral centers, which are almost always tetrahedral (sp³-hybridized) carbons with four different substituents. Consider the cartoon molecule A below: a tetrahedral carbon, with four different substituents denoted by balls of four different colors (for the time being, don't worry about exactly what these substituents could be - we will see real examples very soon).

Another image

The mirror image of A, which we will call B, is drawn on the right side of the figure, and an imaginary mirror is in the middle. Notice that every point on A lines up through the mirror with the same point on B: in other words, if A looked in the mirror, it would see B looking back.

Now, if we flip compound A over and try to superimpose it point for point on compound B, we find that we cannot do it: if we superimpose any two colored balls, then the other two are misaligned.

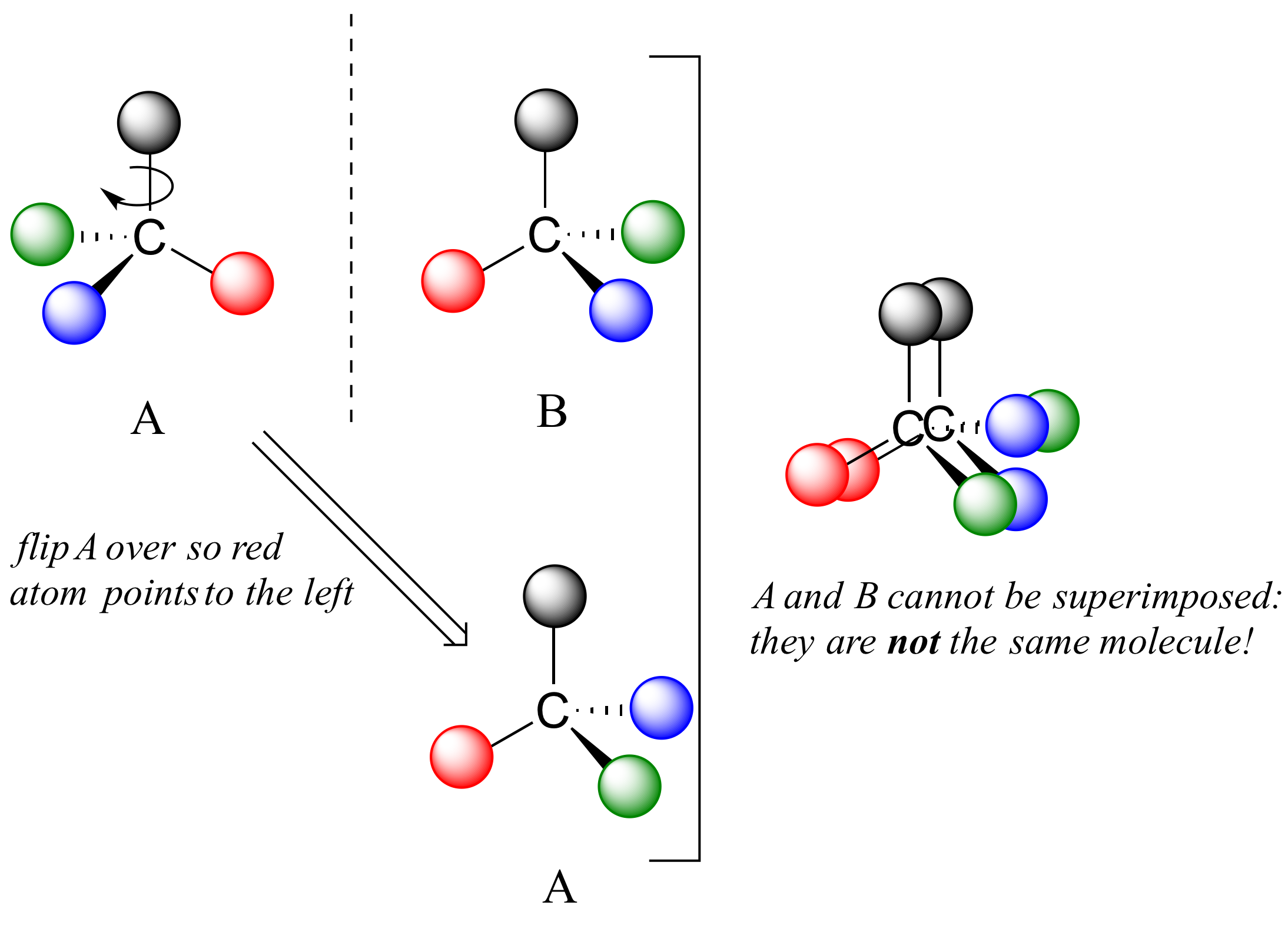
A is not superimposable on its mirror image (B), thus by definition A is a chiral molecule. It follows that B also is not superimposable on its mirror image (A), and thus it is also a chiral molecule. Also notice in the figure below (and convince yourself with models) that neither A nor B has an internal plane of symmetry.

A and B are stereoisomers: molecules with the same molecular formula and the same bonding arrangement, but a different arrangement of atoms in space. There are two types of stereoisomers: enantiomers and diastereomers. Enantiomers are pairs of stereoisomers which are mirror images of each other: thus, A and B are enantiomers. It should be self-evident that a chiral molecule will always have one (and only one) enantiomer: enantiomers come in pairs. Enantiomers have identical physical properties (melting point, boiling point, density, and so on). However, enantiomers do differ in how they interact with polarized light (we will learn more about this soon) and they may also interact in very different ways with other chiral molecules - proteins, for example. We will begin to explore this last idea in later in this chapter, and see many examples throughout the remainder of our study of biological organic chemistry.

Diastereomers are stereoisomers which are not mirror images of each other. For now, we will concentrate on understanding enantiomers, and come back to diastereomers later.

We defined a chiral center as a tetrahedral carbon with four different substituents. If, instead, a tetrahedral carbon has two identical substituents (two black atoms in the cartoon figure below), then of course it still has a mirror image (everything has a mirror image, unless we are talking about a vampire!) However, it is superimposable on its mirror image, and has a plane of symmetry.

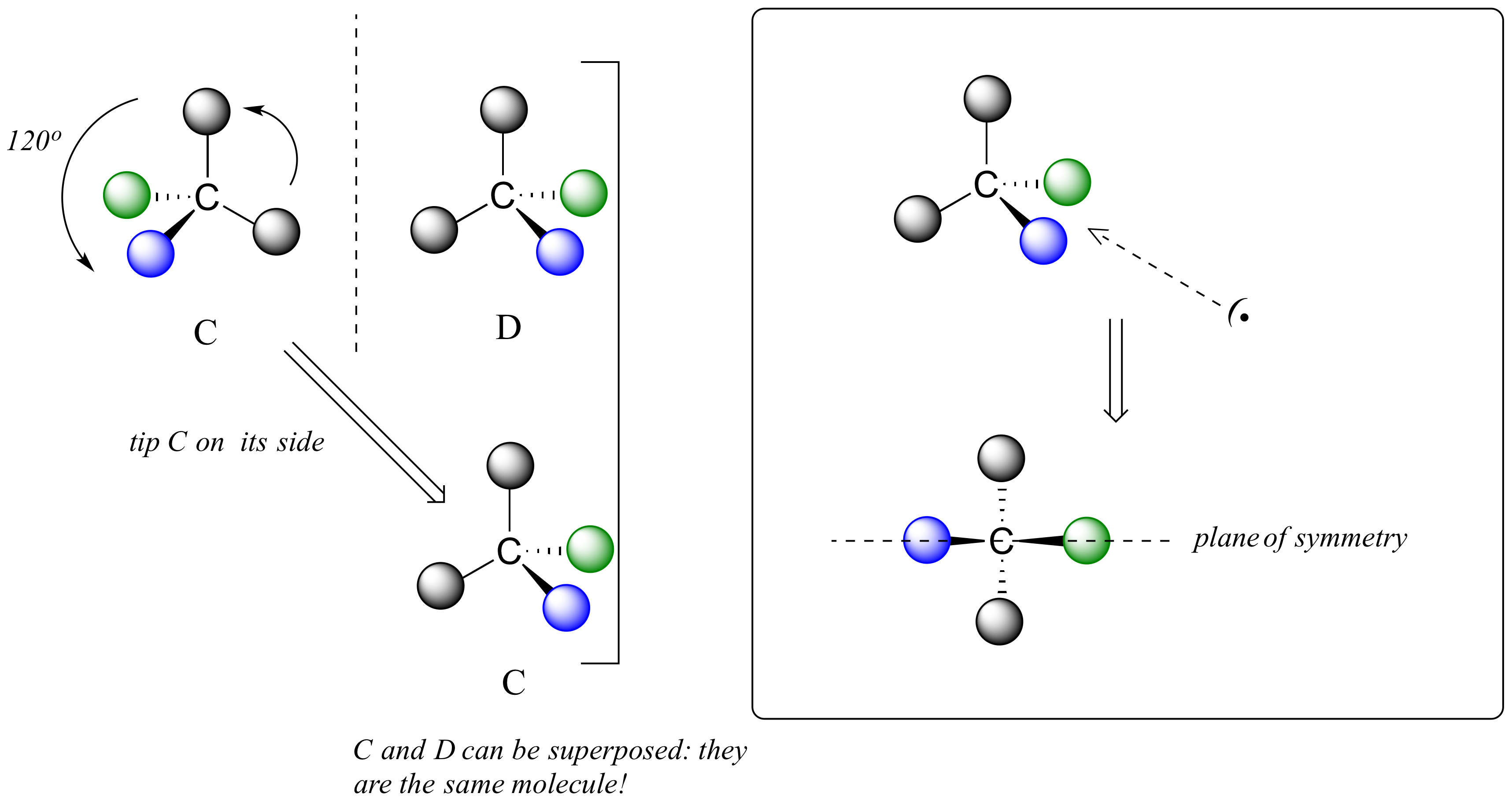
This molecule is achiral (lacking chirality). Using the same reasoning, we can see that a trigonal planar (sp²-hybridized) carbon is also not a chiral center.

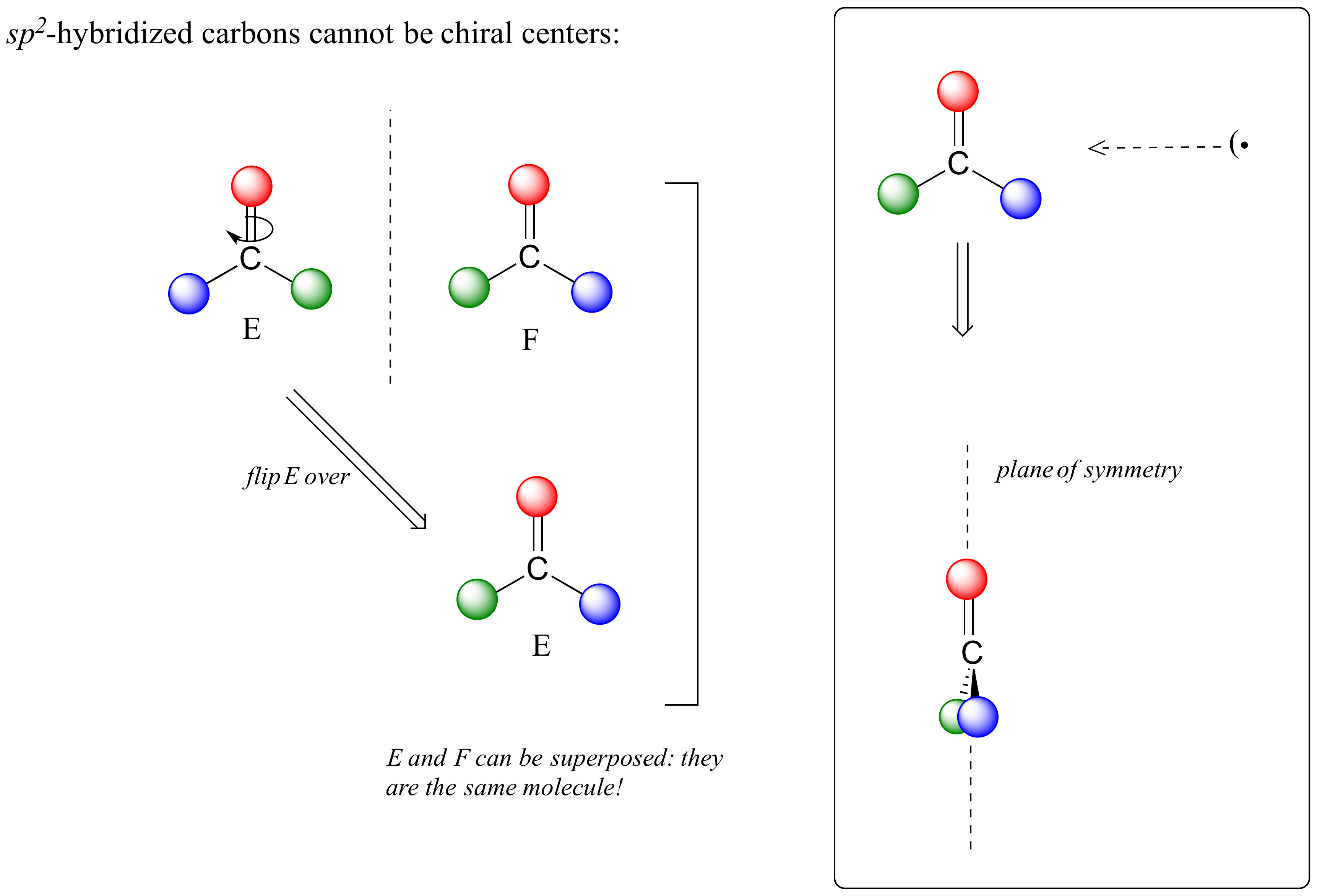
Notice that structure E can be superimposed on F, its mirror image - all you have to do is pick E up, flip it over, and it is the same as F. This molecule has a plane of symmetry, and is achiral.

Let's apply our general discussion to real molecules. For now, we will limit our discussion to molecules with a single chiral center. It turns out that tartaric acid, the subject of our chapter introduction, has two chiral centers, so we will come back to it later.

Consider 2-butanol, drawn in two dimensions below.

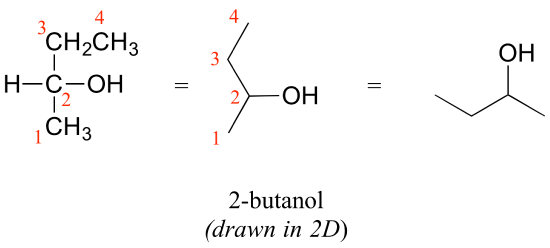
Carbon #2 is a chiral center: it is sp³-hybridized and tetrahedral (even though it is not drawn that way above), and the four things attached to is are different: a hydrogen, a methyl (-CH₃) group, an ethyl (-CH₂CH₃) group, and a hydroxyl (OH) group. Let's draw the bonding at C₂ in three dimensions, and call this structure A. We will also draw the mirror image of A, and call this structure B.

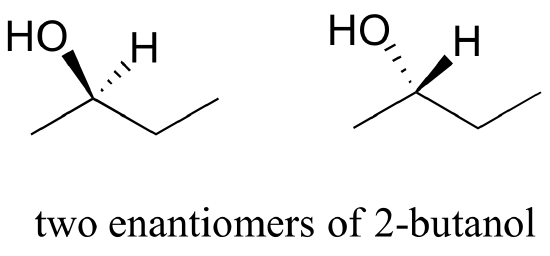
When we try to superimpose A onto B, we find that we cannot do it. A and B are both chiral molecules, and they are enantiomers of each other.

2-propanol, unlike 2-butanol, is not a chiral molecule. Carbon #2 is bonded to two identical substituents (methyl groups), and so it is not a chiral center.

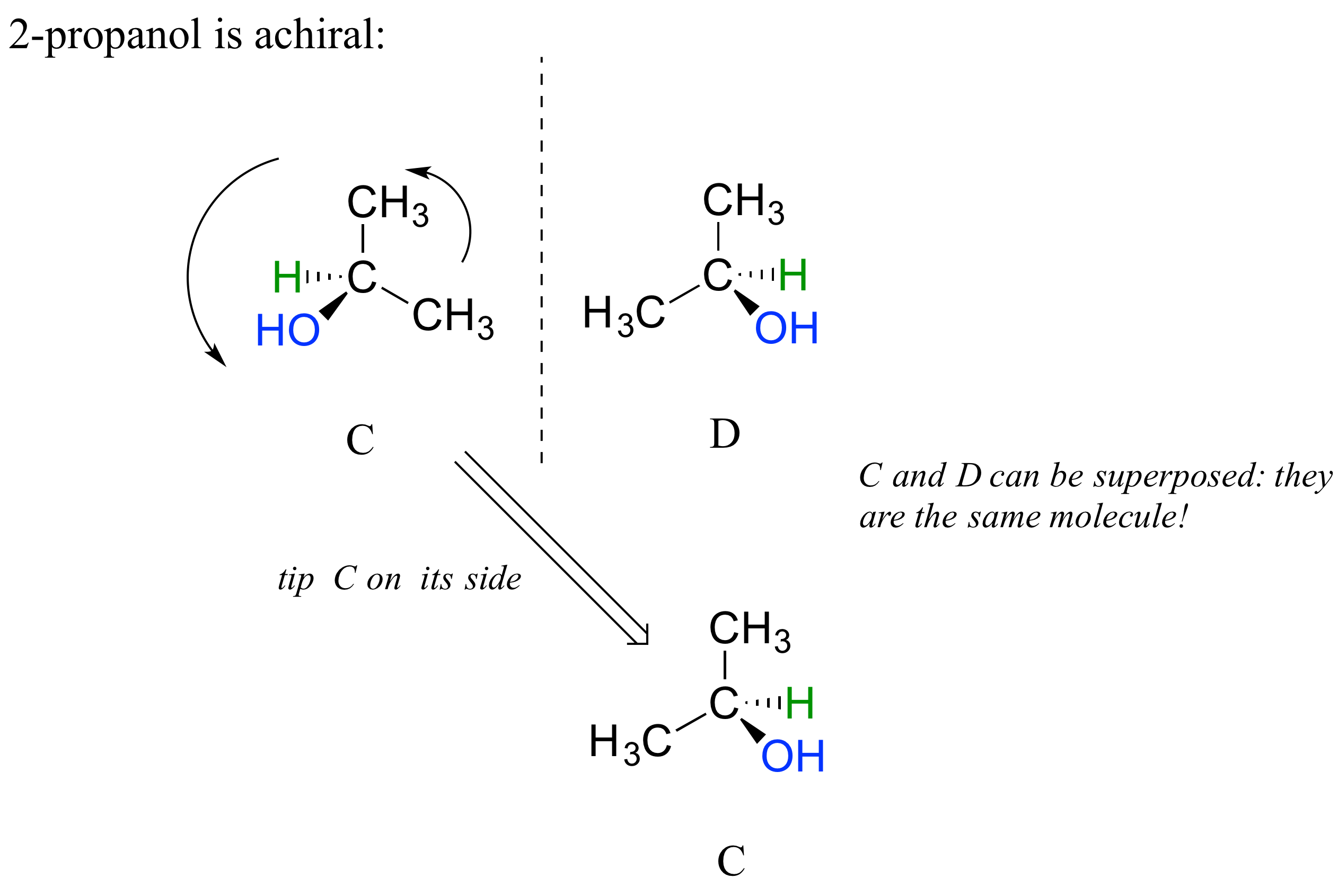
Notice that 2-propanol is superimposable on its own mirror image.

When we look at very simple molecules like 2-butanol, it is not difficult to draw out the mirror image and recognize that it is not superimposable. However, with larger, more complex molecules, this can be a daunting challenge in terms of drawing and three-dimensional visualization. The easy way to determine if a molecule is chiral is simply to look for the presence of one or more chiral centers: molecules with chiral centers will (almost always) be chiral. We insert the 'almost always' caveat here because it is possible to come up with the exception to this rule - we will have more to say on this later, but don't worry about it for now.

Here's another trick to make your stereochemical life easier: if you want to draw the enantiomer of a chiral molecule, it is not necessary to go to the trouble of drawing the point-for-point mirror image, as we have done up to now for purposes of illustration. Instead, keep the carbon skeleton the same, and simply reverse the solid and dashed wedge bonds on the chiral carbon: that accomplishes the same thing. You should use models to convince yourself that this is true, and also to convince yourself that swapping any two substituents about the chiral carbon will result in the formation of the enantiomer.

Here are four more examples of chiral biomolecules, each one shown as a pair of enantiomers, with chiral centers marked by red dots.

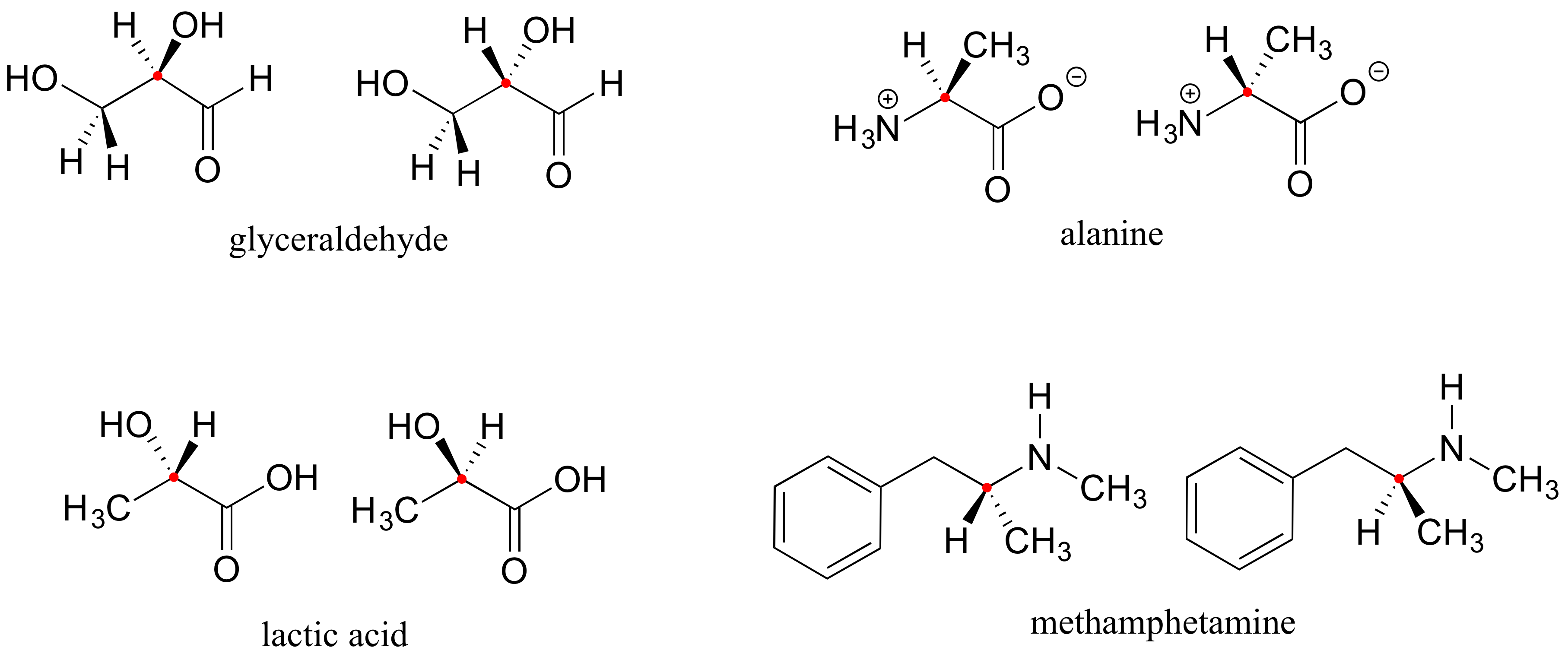
Here are some examples of achiral biomolecules - convince yourself that none of them contain a chiral center:

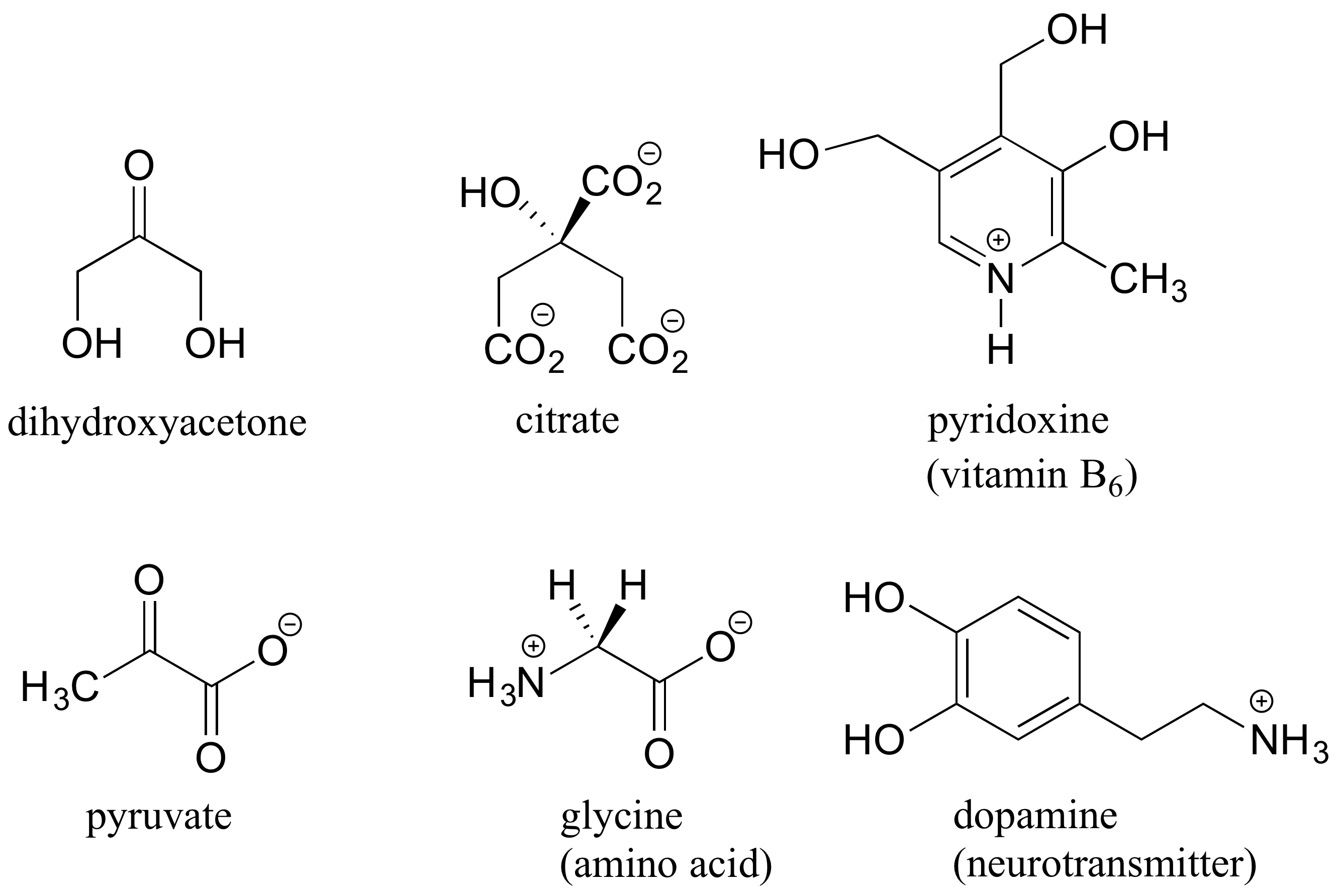
When looking for chiral centers, it is important to recognize that the question of whether or not the dashed/solid wedge drawing convention is used is irrelevant. Chiral molecules are sometimes drawn without using wedges (although obviously this means that stereochemical information is being omitted). Conversely, wedges may be used on carbons that are not chiral centers – look, for example, at the drawings of glycine and citrate in the figure above.

Can a chiral center be something other than a tetrahedral carbon with four different substituents? The answer to this question is 'yes' - however, these alternative chiral centers are very rare in the context of biological organic chemistry, and outside the scope of our discussion here.

You may also have wondered about amines: shouldn't we consider a secondary or tertiary amine to be a chiral center, as they are tetrahedral and attached to four different substituents, if the lone-pair electrons are counted as a 'substituent'? Put another way, isn't an amine non-superimposable on its mirror image?

The answer: yes it is, in the static picture, but in reality, the nitrogen of an amine is rapidly and reversibly inverting, or turning inside out, at room temperature.

If you have trouble picturing this, take an old tennis ball and cut it in half. Then, take one of the concave halves and flip it inside out, then back again: this is what the amine is doing. The end result is that the two 'enantiomers' if the amine are actually two rapidly interconverting forms of the same molecule, and thus the amine itself is not a chiral center. This inversion process does not take place on a tetrahedral carbon, which of course has no lone-pair electrons.

Exercise 3.8

Locate all of the chiral centers (there may be more than one in a molecule). Remember, hydrogen atoms bonded to carbon usually are not drawn in the line structure convention - but they are still there!

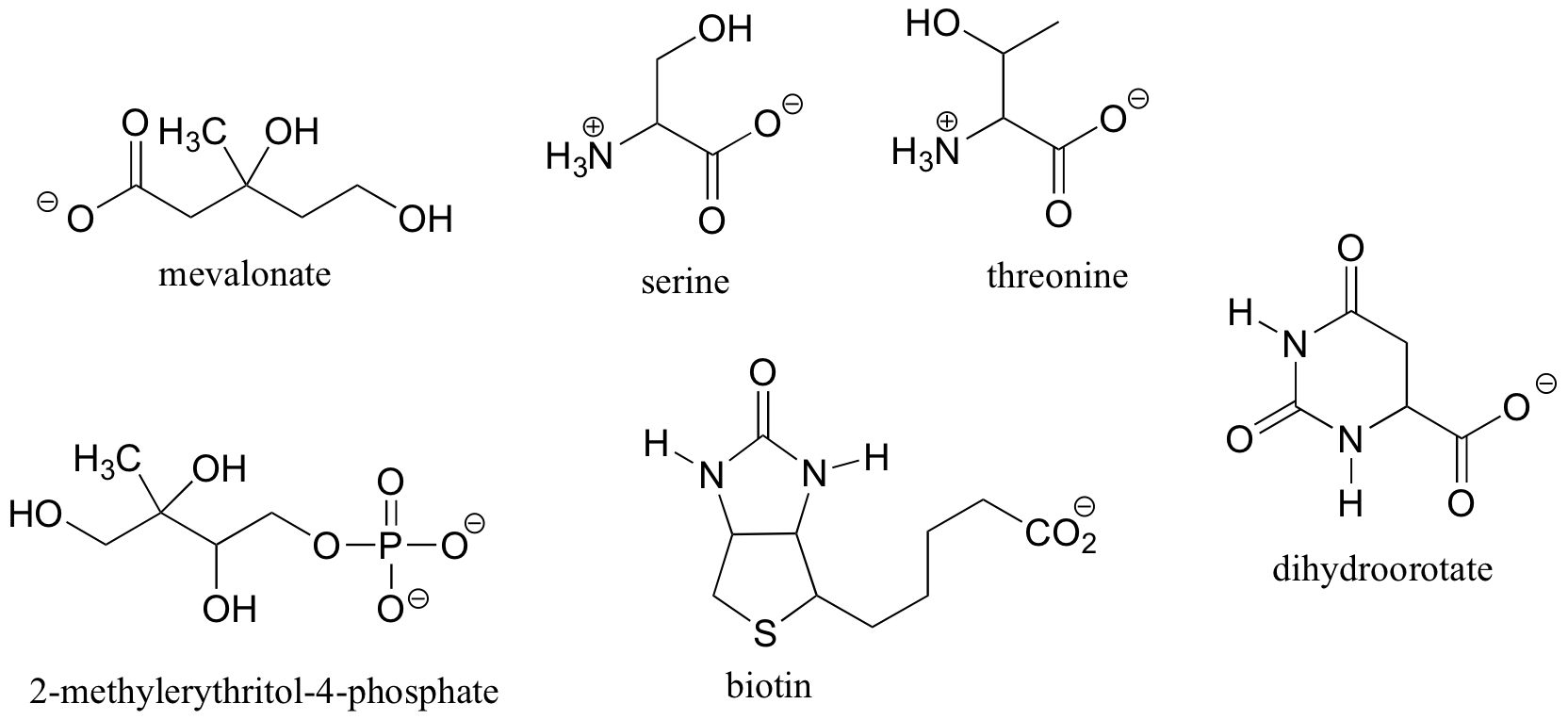
Exercise 3.9

a) Draw two enantiomers of i) mevalonate and ii) serine.

b) Are the two 2-butanol structures below enantiomers?

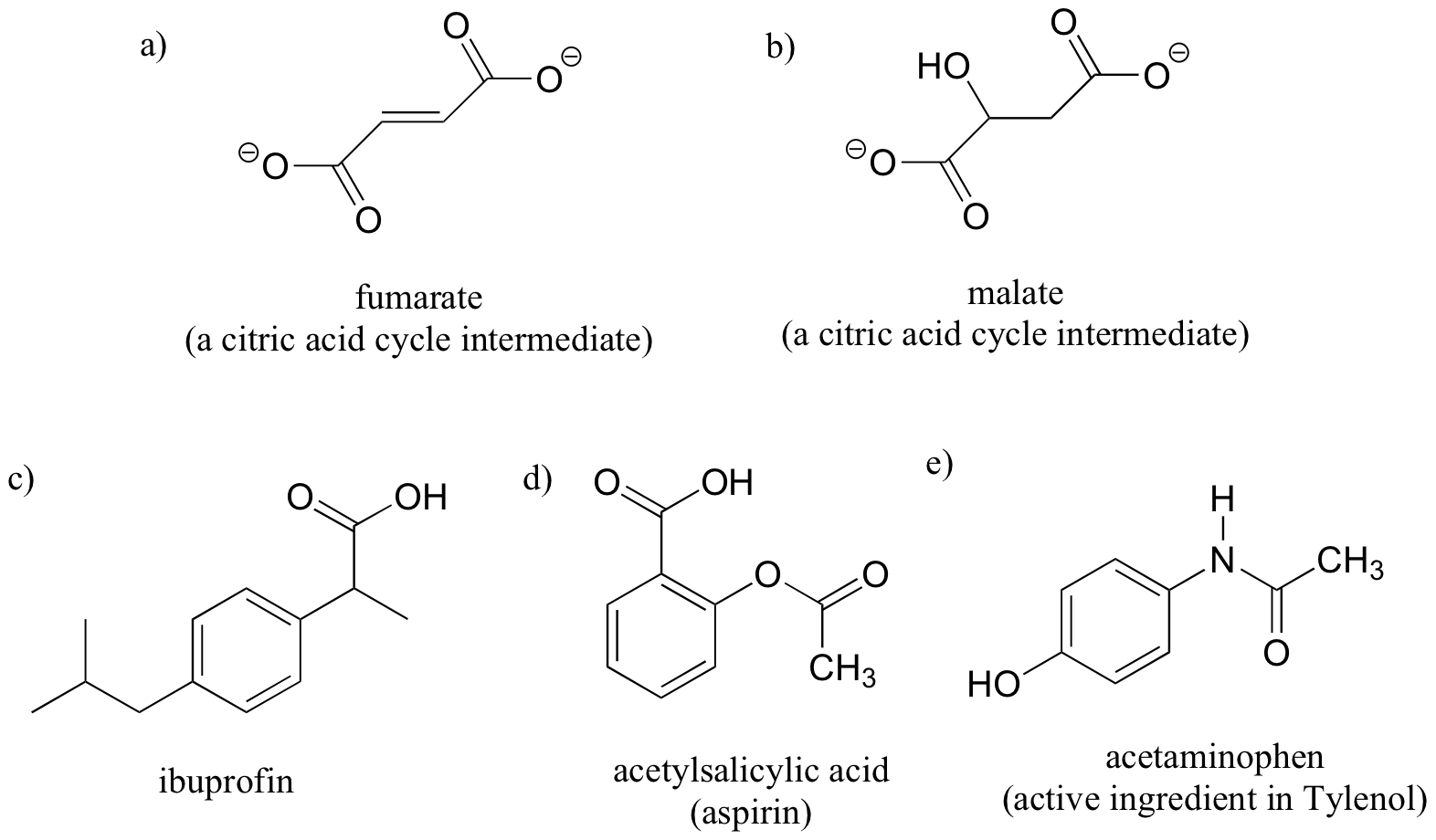
Exercise 3.10

Label the molecules below as chiral or achiral, and locate all chiral centers.

Solutions to exercises

Khan Academy video tutorials

Chirality

Enantiomers