Now it is finally time to put together all that we have studied about structure determination techniques and learn how to actually solve the structure of an organic molecule 'from scratch' - starting, in other words, with nothing but the raw experimental data. For this exercise, we will imagine that we have been given a vial containing a pure sample of an unknown organic compound, and that this compound to our knowledge has never before been synthesized, isolated, or characterized - we are the first to get our hands on it. Can we figure out its structure? While of course the exact method of determining an unknown structure will depend on the compound in question and, in the real world of research, will probably involve some techniques that are beyond the scope of this book, here is an overview of an approach that could be taken to analyze a pure sample of a relatively simple organic compound, using the techniques we have learned about.
Step 1: Use MS and combustion analysis to determine the molecular formula
Before we start analyzing spectroscopic data, we need one very important piece of information about our compound - its molecular formula. This can be determined through the combined use of mass spectrometry and combustion analysis. We will not go into the details of combustion analysis - for now, it is enough to know that this technique tells us the mass percent of each element in the compound. Because molecular oxygen is involved in the combustion reaction, oxygen in the sample is not measured directly - but we assume that if the mass percentages do not add up to 100%, the remainder is accounted for by oxygen.
When we obtain our unknown compound, one of the first things we will do is to send away a small quantity to an analytical company specializing in combustion analysis. They send us back a report stating that our compound is composed, by mass, of 52.0% carbon, 38.3% chlorine, and 9.7% hydrogen. This adds up to 100%, so our compound does not contain any oxygen atoms.
In order to determined the molecular formula of our compound from this data, we first need to know its molar mass. This piece of information, as you recall from chapter 4, we determine by looking at the 'molecular ion peak' in the mass spectrum of our compound. In this example, we find that our MS data shows a molecular ion peak at m/z = 92, giving us a molar mass of 92 g/mole (remember that in the MS experiment, charge (z) is almost always equal to 1, because we are looking at +1 cations).
So, one mole of our compound is 92g. How many moles of carbon atoms are in one mole of the compound? Simple: 52% of 92g is 47.8g. So in one mole of our compound, there is about 48 g of carbon, which means four moles of carbon. With similar calculations, we find that one mole of our compound contains nine hydrogens and one chlorine. Therefore our molecular formula is \(C_4H_9Cl\).
Step 2: Calculate the Index of Hydrogen Deficiency
The next step is to calculate a number called the Index of Hydrogen Deficiency (IHD) from the molecular formula. The IHD will tell us how many multiple bonds and/or ring structures our molecule has - very useful information. The idea behind the IHD is very simple: the presence of a double bond or a ring structure means that two fewer hydrogen atoms can be part of the compound. The formula for calculating IHD from a molecular formula is:
Calculating Index of Hydrogen Deficiency:
\[IHD = \frac{(2n+2) - A}{2}\]
where:
n = number of carbon atoms
A = (number of hydrogen atoms) + (number of halogen atoms) - (number of nitrogen atoms) - (net charge)
For example, a molecule with the molecular formula \(C_6H_{14}\) would have n = 6 and A = 14, so we can calculate that IHD = 0 and thereby know that a compound with this formula has no double bonds or ring structures. Hexane and 2-methyl pentane are two examples of compounds that apply.
A molecular formula of \(C_6H_{12}\), on the other hand, corresponds to IHD = 1, so a compound with this formula should have one double bond or one ring structure. Cyclohexane (one ring structure) and 2-hexene (one double bond) are two possibilities. Benzene (\(C_6H_6\)) , and methyl benzene (\(C_7H_8\)) both have IHD = 4, corresponding in both cases to three p bonds and one ring. An IHD value of 4 or greater is often an indicator that an aromatic ring is present.
- What is the IHD that corresponds to a molecular formula \(C_6H_{12}O\)? Draw the structures of three possible compounds that fit.
- The amino acid alanine has molecular formula \(C_2H_8NO_2^+\) in aqueous buffer of \(pH = 2\). Calculate the IHD. Then, draw the relevant structure to confirm that this IHD makes sense.
- What is the IHD of the compounds below? (Hint: you don't need to figure out molecular formulas!)

The formula for our structure determination sample, \(C_4H_9Cl\), corresponds to IHD = 0, meaning that our compound contains no multiple bonds or rings.
Step 3: Use available spectroscopy data to identify discrete parts of the structure.
In this problem, we have proton and carbon \(NMR\) data to work with (other problems may include IR and/or UV/Vis data).
\(^1H-NMR\)
| ppm |
splitting |
integration |
| 3.38 |
d |
2 |
| 1.95 |
m |
1 |
| 1.01 |
d |
6 |
\(^{13}C-NMR\):
52.49 (\(CH_2\))
31.06 (\(CH\))
20.08 (\(CH_3\))
The process of piecing together an organic structure is very much like putting together a puzzle. In every case we start the same way, determining the molecular formula and the IHD value. After that,
there is no set formula for success- what we need to do is figure out as much as we can about individual pieces of the molecule from the \(NMR\) (and often IR, MS, or UV-Vis) data, and write these down. Eventually, hopefully, we will be able to put these pieces together in a way that agrees with all of our empirical data. Let's give it a go.
We see that there are only three signals in each \(NMR\) spectrum, but four carbons in the molecule, which tells us that two of the carbons are chemically equivalent. The fact that the signal at 1.01 ppm in the proton spectrum corresponds to six protons strongly suggests that the molecule has two equivalent methyl (\(CH_3\)) groups. Because this signal is a doublet, there must be a \(CH\) carbon bound to each of these two methyl groups. Taken together, this suggests:

The \(^1H-NMR\) signal at 3.38 ppm must be for protons bound to the carbon which is in turn bound to the chlorine (we infer this because this signal is the furthest downfield in the spectrum, due to the deshielding effect of the electronegative chlorine). This signal is for two protons and is a doublet, meaning that there is a single nonequivalent proton on an adjacent carbon.
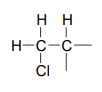
Step 4: Try to put the pieces of the puzzle together, and see if everything fits the available data.
At this point, we have accounted for all of the atoms in the structure, and we have enough information to put together a structure that corresponds to 1-chloro-2-methylpropane.

To confirm, we make assignment all \(NMR\) signals to their corresponding atoms and make sure that our structure fits all of the \(NMR\) data. Notice that the proton peak at 1.95 ppm might be expected to be a '9-tet' because of its eight 3-bond neighbors: however, two of the neighbors are different from the other six, and may not couple to exactly the same extent. The signal at 1.95 will not, then, be a 'clean' 9-tet, and we would call it a multiplet.
Three constitutional isomers of 1-chloro-2-methylpropane produce the following NMR data. Assign structures to the three compounds, and make all peak assignments.
- Compound A: (2-chloro-2-methylpropane)
\(^1H-NMR\):
1.62 ppm, \(9H\), s
\(^{13}C-NMR\):
67.14 ppm (\(C\))
34.47 ppm (\(CH_3\))
- Compound B: (1-chlorobutane)
\(^1H-NMR\):
3.42 ppm, \(2H\), t
1.68 ppm, \(2H\), p
1.41 ppm, \(2H\), sextet
0.92 ppm, \(3H\), t
\(^{13}C-NMR\):
44.74 ppm (\(CH_2\))
34.84 ppm (\(CH_2\))
20.18 ppm (\(CH_2\))
13.34 ppm (\(CH_3\))
- Compound C: (2-chlorobutane)
\(^1H-NMR\):
3.97 ppm, \(1H\), sextet
1.71 ppm, \(2H\), p
1.50 ppm, \(3H\), d
1.02 ppm, \(3H\), t
\(^{13}C-NMR\):
60.34 ppm (\(CH\))
33.45 ppm (\(CH_2\))
24.94 ppm (\(CH_3\))
11.08 ppm (\(CH_3\))
Let's try another problem, this time incorporating IR information.
The following data was obtained for a pure sample of an unknown organic compound:
Combustion analysis:
\(C\): 85.7%
\(H\): 6.67%
MS: Molecular ion at m/z = 210
\(^1H-NMR\):
7.5-7.0, 10H, m
5.10, 1H, s
2.22, 3H, s
\(^{13}C-NMR\):
206.2 (\(C\)) 128.7 (\(CH\)) 30.0 (\(CH_3\))
138.4 (\(C\)) 127.2 (\(CH\))
129.0 (\(CH\)) 65.0 (\(CH\))
IR: 1720 cm-1, strong (there are of course many other peaks in the IR spectrum, but this is the most characteristic one)
The molecular weight is 210, and we can determine from combustion analysis that the molecular formula is \(C_{15}H_{14}O\) (the mass percent of oxygen in the compound is assumed to be 100 - 85.7 - 6.67 = 7.6 %). This gives us IHD = 9.
Because we have ten protons with signals in the aromatic region (7.5-7.0 ppm), we are probably dealing with two phenyl groups, each with one substituted carbon. The \(^{13}C-NMR\) spectrum shows only four signals in the range for aromatic carbons, which tells us that the two phenyl groups must be in equivalent electronic environments (if they are in different environments, they would give rise to eight signals).
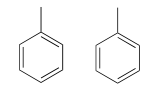
This accounts for 12 carbons, 10 hydrogens, and 8 IHD units. Notice that the carbon spectrum has only six peaks - and only four peaks in the aromatic region! This again indicates that the two phenyl groups are in chemically equivalent positions
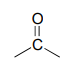
The IR spectrum has a characteristic carbonyl absorption band, so that accounts for the oxygen atom in the molecular formula, the one remaining IHD unit, and the \(^{13}C-NMR\) signal at 206.2 ppm.
Now we only have two carbons and four hydrogens left to account for. The proton spectrum tells us we have a methyl group (the 2.22 ppm singlet) that is not split by neighboring protons. Looking at the table of typical chemical shifts, we see that this chemical shift value is in the range of a carbon next to a carbonyl.
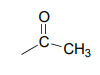
Finally, there is one last proton at 5.10 ppm, also a singlet. Putting the puzzle together, the only possibility that fits is 1,1-diphenyl-2-propanone:

fig 43
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.










