2.3: The Acidity Constant
- Last updated
- Save as PDF
- Page ID
- 170418
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Defining the acidity constant
You are no doubt aware that some acids are stronger than others. The relative acidity of different compounds or functional groups – in other words, their relative capacity to donate a proton to a common base under identical conditions – is quantified by a number called the acidity constant, abbreviated \(K_a\). The common base chosen for comparison is water.
We will consider acetic acid as our first example. If we make a dilute solution of acetic acid in water, an acid-base reaction occurs between the acid (proton donor) and water (proton acceptor).

Acetic acid is a weak acid, so the equilibrium favors reactants over products - it is thermodynamically 'uphill'. This is indicated in the figure above by the relative length of the forward and reverse reaction arrows.
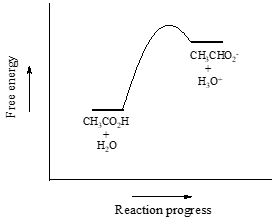
The equilibrium constant \(K_{eq}\) is defined as:
\[K_{eq} = \frac{[\text{products}]}{[\text{reactants}]} = \frac{[CH_3COO^-][H_3O^+]}{[CH_3COOH][H_2O]}\]
Remember that this is a dilute aqueous solution: we added a small amount of acetic acid to a large amount of water. Therefore, in the course of the reaction, the concentration of water (approximately 55.6 mol/L) changes very little, and can be treated as a constant.
If we move the constant term for the concentration of water to the left side of the equilibrium constant expression, we get the expression for \(K_a\), the acid constant for acetic acid:
\[K_a = K_{eq}[H_2O] = \frac{[CH_3COO^-][H_3O^+]}{[CH_3COOH]}\]
In more general terms, the dissociation constant for a given acid HA or HB+ is expressed as:
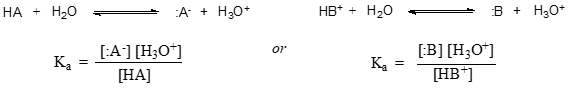
The value of \(K_a\) for acetic acid is \(1.75 \times 10^{-5}\) - much less than \(1\), indicating there is much more acetic acid in solution at equilibrium than acetate and hydronium ions.
Conversely, sulfuric acid, with a \(K_a\) of approximately \(10^9\), or hydrochloric acid, with a \(K_a\) of approximately \(10^7\), both undergo essentially complete dissociation in water: they are very strong acids.
A number like \(1.75 \times 10^{- 5}\) is not very easy either to say, remember, or visualize, so chemists usually use a more convenient term to express relative acidity. The \(pK_a\) value of an acid is simply the log (base 10) of its \(K_a\) value.
\[pK_a = -log K_a \qquad K_a = 10^{-pK_a}\]
Doing the math, we find that the \(pK_a\) of acetic acid is \(4.8\). The \(pK_a\) of sulfuric acid is -10, and of hydrochloric acid is -7. The use of \(pK_a\) values allows us to express the relative acidity of common compounds and functional groups on a numerical scale of about –10 (for a very strong acid) to 50 (for a compound that is not acidic at all). The lower the \(pK_a\) value, the stronger the acid.
The ionizable (proton donating or accepting) functional groups relevant to biological organic chemistry generally have \(pK_a\) values ranging from about 5 to about 20. The most important of these are summarized below, with very rough \(pK_a\) values for the conjugate acid forms. More acidic groups with \(pK_a\) values near zero are also included for reference.
Typical \(pK_a\) values
| group | approximate \(pK_a\) |
|---|---|
| hydronium ion | 0 |
| protonated alcohol | 0 |
| protonated carbonyl | 0 |
| carboxylic acids | 5 |
| protonated imines | 7 |
| protonated amines | 10 |
| phenols | 10 |
| thiols | 10 |
| alcohols, water | 15 |
| \(\alpha\)-carbon acids * | 20 |
*\(\alpha\)-carbon acids will be explained in section 7.6A
It is highly recommended to commit these rough values to memory now - then if you need a more precise value, you can always look it up in a more complete \(pK_a\) table. The appendix to this book contains a more detailed table of typical \(pK_a\) values, and much more complete tables are available in resources such as the Handbook of Chemistry and Physics.
\(pK_a\) vs. \(pH\)
It is important to realize that \(pK_a\) is not the same thing as \(pH\): the former is an inherent property of a compound or functional group, while the latter is a measure of hydronium ion concentration in a given aqueous solution:
\[pH = -log [H_3O^+]\]
Knowing \(pK_a\) values not only allows us to compare acid strength, it also allows us to compare base strength. The key idea to remember is this: the stronger the conjugate acid, the weaker the conjugate base. We can determine that hydroxide ion is a stronger base than ammonia (\(NH_3\)), because ammonium ion (\(NH4^+\), \(pK_a = 9.2\)) is a stronger acid than water (\(pK_a = 15.7\)).
Exercise 7.3.1
Which is the stronger base, \(CH_3O^-\) or \(CH_3S^-\)? Acetate ion or ammonia? Hydroxide ion or acetate ion?
Let's put our understanding of the \(pK_a\) concept to use in the context of a more complex molecule. For example, what is the \(pK_a\) of the compound below?

We need to evaluate the potential acidity of four different types of protons on the molecule, and find the most acidic one. The aromatic protons are not all acidic - their \(pK_a\) is about 45. The amine group is also not acidic, its \(pK_a\) is about 35. (Remember, uncharged amines are basic: it is positively-charged protonated amines, with \(pK_a\) values around 10, that are weakly acidic.) The alcohol proton has a \(pK_a\) of about 15, and the phenol proton has a \(pK_a\) of about 10: thus, the most acidic group on the molecule above is the phenol. (Be sure that you can recognize the difference between a phenol and an alcohol - remember, in a phenol the \(OH\) group is bound directly to the aromatic ring). If this molecule were to react with one molar equivalent of a strong base such as sodium hydroxide, it is the phenol proton which would be donated to form a phenolate anion.
Exercise 7.3.2
Identify the most acidic functional group on each of the molecules below, and give its approximate \(pK_a\).
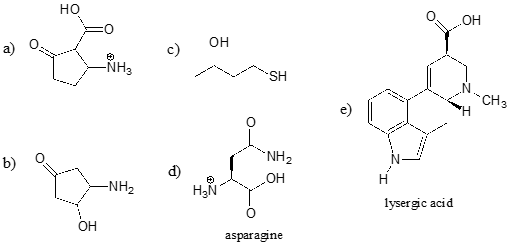
Using \(pK_a\) values to predict reaction equilibria
By definition, the \(pK_a\) value tells us the extent to which an acid will react with water as the base, but by extension we can also calculate the equilibrium constant for a reaction between any acid-base pair. Mathematically, it can be shown that:
\[K_{eq} = 10^{\Delta pK_a}\]
\[\Delta pK_a = \text{(pKa of product acid minus pKa of reactant acid)}\]
Consider a reaction between methylamine and acetic acid:
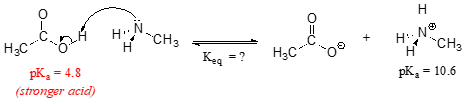
The first step is to identify the acid species on either side of the equation, and look up or estimate their \(pK_a\) values. On the left side, the acid is of course acetic acid while on the right side the acid is methyl ammonium ion (in other words, methyl ammonium ion is the acid in the reaction going from right to left). We can look up the precise \(pK_a\) values in table 7 (at the back of the book), but we already know (because we have this information memorized, right?!) that the \(pK_a\) of acetic acids is about 5, and methyl ammonium is about 10. More precise values are 4.8 and 10.6, respectively.
Without performing any calculations at all, you should be able to see that this equilibrium lies far to the right-hand side: acetic acid has a lower \(pK_a\), meaning it is a stronger acid than methyl ammonium, and thus it wants to give up its proton more than methyl ammonium does. Doing the math, we see that
\[K_{eq} = 10^{\Delta pK_a} = 10^{(10.6 - 4.8)} = 10^{5.8} = 6.3 \times 10^5\]
So \(K_{eq}\) is a very large number (much greater than 1) and the equilibrium for the reaction between acetic acid and methylamine lies far to the right-hand side of the equation, just as we had predicted. This also tells us that the reaction has a negative Gibbs free energy change, and is thermodynamically favorable.

If you had just wanted to quickly approximate the value of \(K_{eq}\) without benefit of precise \(pK_a\) information or a calculator, you could have approximated \(pK_a ~ 5\) (for the carboxylic acid) and \(pK_a ~10\) (for the ammonium ion) and calculated in your head that the equilibrium constant should be somewhere in the order of \(10^5\).
Exercise 7.3.3
Show the products of the following acid-base reactions, and roughly estimate the value of \(K_{eq}\).

Organic molecules in buffered solution: the Henderson-Hasselbalch equation
The environment inside a living cell, where most biochemical reactions take place, is an aqueous buffer with \(pH ~ 7\). Recall from your General Chemistry course that a buffer is a solution of a weak acid and its conjugate base. The key equation for working with buffers is the Henderson-Hasselbalch equation:
The Henderson-Hasselbalch equation
\[pH = pK_a + \log \left ( \frac{\text{concentration of conjugate base}}{\text{concentration of weak acid}} \right )\]
The equation tells us that if our buffer is an equimolar solution of a weak acid and its conjugate base, the \(pH\) of the buffer will equal the \(pK_a\) of the acid (because the log of 1 is equal to zero). If there is more of the acid form than the base, then of course the \(pH\) of the buffer is lower than the \(pK_a\) of the acid.
Exercise 7.3.4
What is the pH of an aqueous buffer solution that is 30 mM in acetic acid and 40 mM in sodium acetate? The pKa of acetic acid is 4.8.
The Henderson-Hasselbalch equation is particularly useful when we want to think about the protonation state of different biomolecule functional groups in a \(pH 7\) buffer. When we do this, we are always assuming that the concentration of the biomolecule is small compared to the concentration of the buffer components. (The actual composition of physiological buffer is complex, but it is primarily based on phosphoric and carbonic acids).
Imagine an aspartic acid residue located on the surface of a protein in a human cell. Being on the surface, the side chain is in full contact with the \(pH 7\) buffer surrounding the protein. In what state is the side chain functional group: the protonated state (a carboxylic acid) or the deprotonated state (a carboxylate ion)? Using the Henderson-Hasselbalch equation, we fill in our values for the \(pH\) of the buffer and a rough \(pK_a\) approximation of \(pK_a = 5\) for the carboxylic acid functional group. Doing the math, we find that the ratio of carboxylate to carboxylic acid is about 100 to 1: the carboxylic acid is almost completely ionized (in the deprotonated state) inside the cell. This result extends to all other carboxylic acid groups you might find on natural biomolecules or drug molecules: in the physiological environment, carboxylic acids are almost completely deprotonated.
Now, let's use the equation again, this time for an amine functional group, such as the side chain of a lysine residue: inside a cell, are we likely to see a neutral amine (\(R-NH_2\)) or an ammonium cation (\(R-NH_3^+\)?) Using the equation with \(pH = 7\) (for the biological buffer) and \(pK_a = 10\) (for the ammonium group), we find that the ratio of neutral amine to ammonium cation is about 1 to 100: the group is close to completely protonated inside the cell, so we will see \(R-NH_3^+\), not \(R-NH_2\).
We can do the same rough calculation for other common functional groups found in biomolecules.
Note
At physiological \(pH\):
Carboxylic acids are deprotonated (in the carboxylate anion form)
Amines are protonated (in the ammonium cation form)
Thiols, phenols, alcohols, and amides are uncharged
Imines are a mixture of the protonated (cationic) and deprotonated (neutral) states.
We will talk about the physiological protonation state of phosphate groups in chapter 9.
Exercise 7.3.5
The molecule below is not drawn in the protonation state that we would expect to see it at physiological \(pH\). Redraw it in the physiologically relevant protonation state.

While we are most interested in the state of molecules at \(pH 7\), the Henderson-Hasselbalch equation can of course be used to determine the protonation state of functional groups in solutions buffered to other \(pH\) levels. The exercises below provide some practice in this type of calculation.
Exercise 7.3.6
What is the ratio of acetate ion to neutral acetic acid when a small amount of acetic acid \(pK_a = 4.8\) is dissolved in a buffer of \(pH 2.8\)? \(pH 3.8\)? \(pH 4.8\)? \(pH 5.8\)? \(pH 6.8\)?
Exercise 7.3.7
Would you expect phenol to be soluble in an aqueous solution buffered to \(pH 2\)? \(pH 7\)? \(pH 12\)? Explain your answer.
Exercise 7.3.8
Methylamine is dissolved in a \(pH 9.0\) buffer. What percent of the solute molecules are charged? What is the average charge on solute molecules?
Exercise 7.3.9
What is the approximate net charge on a tetrapeptide Cys-Asp-Lys-Glu in \(pH 7\) buffer?


