3.1: Intermolecular Interactions (Ball)
- Last updated
- Save as PDF
- Page ID
- 239771
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Define phase.
- Identify the types of interactions between molecules.
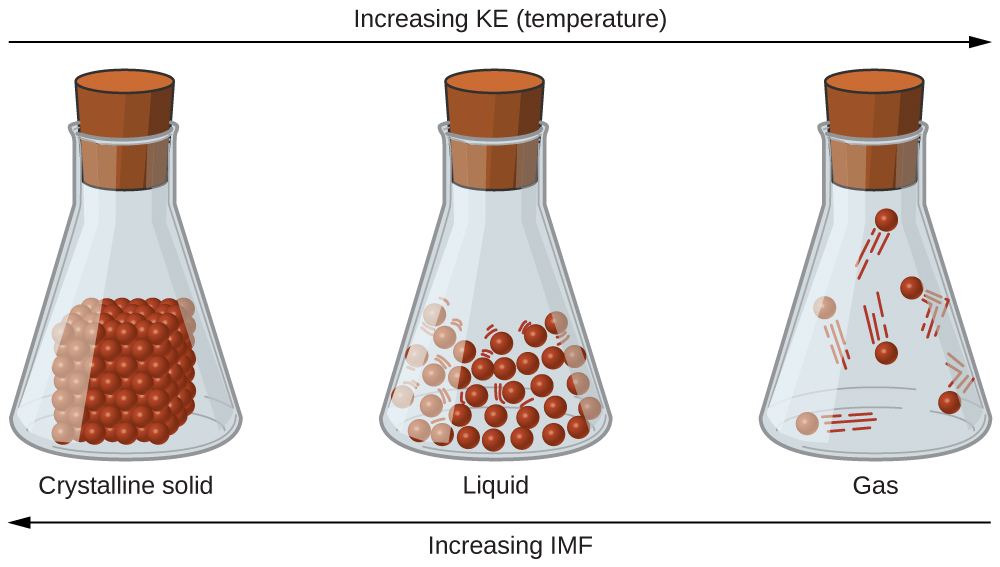
A phase is a certain form of matter that includes a specific set of physical properties. That is, the atoms, the molecules, or the ions that make up the phase do so in a consistent manner throughout the phase. Science recognizes three stable phases: the solid phase, in which individual particles can be thought of as in contact and held in place; the liquid phase, in which individual particles are in contact but moving with respect to each other; and the gas phase, in which individual particles are separated from each other by relatively large distances (see Figure 8.1.1). Not all substances will readily exhibit all phases. For example, carbon dioxide does not exhibit a liquid phase unless the pressure is greater than about six times normal atmospheric pressure. Other substances, especially complex organic molecules, may decompose at higher temperatures, rather than becoming a liquid or a gas.
For many substances, there are different arrangements the particles can take in the solid phase, depending on temperature and pressure.
Which phase a substance adopts depends on the pressure and the temperature it experiences. Of these two conditions, temperature variations are more obviously related to the phase of a substance. When it is very cold, H2O exists in the solid form as ice. When it is warmer, the liquid phase of H2O is present. At even higher temperatures, H2O boils and becomes steam.
Pressure changes can also affect the presence of a particular phase (as we indicated for carbon dioxide), but its effects are less obvious most of the time. We will mostly focus on the temperature effects on phases, mentioning pressure effects only when they are important. Most chemical substances follow the same pattern of phases when going from a low temperature to a high temperature: the solid phase, then the liquid phase, and then the gas phase. However, the temperatures at which these phases are present differ for all substances and can be rather extreme. Table \(\PageIndex{1}\) shows the temperature ranges for solid, liquid, and gas phases for three substances. As you can see, there is extreme variability in the temperature ranges.
| Substance | Solid Phase Below | Liquid Phase Above | Gas Phase Above |
|---|---|---|---|
| hydrogen (H2) | −259°C | −259°C | −253°C |
| water (H2O) | 0°C | 0°C | 100°C |
| sodium chloride (NaCl) | 801°C | 801°C | 1413°C |
| The melting point of a substance is the temperature that separates a solid and a liquid. The boiling point of a substance is the temperature that separates a liquid and a gas. | |||
What accounts for this variability? Why do some substances become liquids at very low temperatures, while others require very high temperatures before they become liquids? It all depends on the strength of the intermolecular forces (IMF) between the particles of substances and the kinetic energies (KE) of its molecules. (Although ionic compounds are not composed of discrete molecules, we will still use the term intermolecular to include interactions between the ions in such compounds.) Substances that experience strong intermolecular interactions require higher temperatures to become liquids and, finally, gases. Substances that experience weak intermolecular interactions do not need much energy (as measured by temperature) to become liquids and gases and will exhibit these phases at lower temperatures.
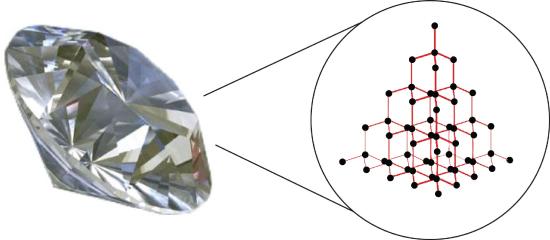
Covalent Network Materials
Substances with the highest melting and boiling points have covalent network bonding. This type of intermolecular interaction is actually a covalent bond. In these substances, all the atoms in a sample are covalently bonded to one another; in effect, the entire sample is essentially one giant molecule. Many of these substances are solid over a large temperature range because it takes a lot of energy to disrupt all the covalent bonds at once. One example of a substance that shows covalent network bonding is diamond (Figure \(\PageIndex{2}\)). Diamond is composed entirely of carbon atoms, each bonded to four other carbon atoms in a tetrahedral geometry. Melting a covalent network solid is not accomplished by overcoming the relatively weak intermolecular forces. Rather, all of the covalent bonds must be broken, a process that requires extremely high temperatures. Diamond, in fact, does not melt at all. Instead, it vaporizes to a gas at temperatures above 3,500°C. Diamond is extremely hard and is one of the few materials that can cut glass.
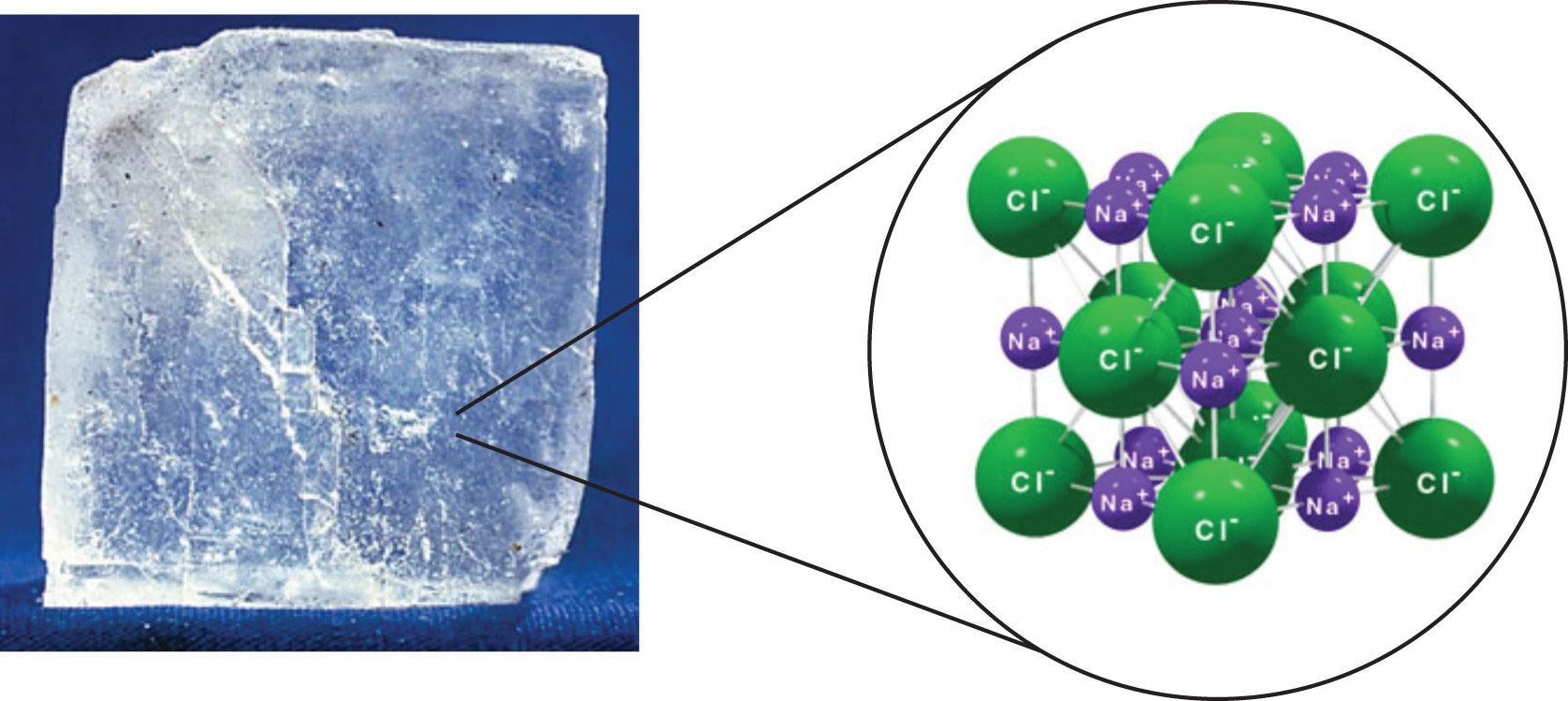
Ionic Compounds
The strongest force between any two particles is the ionic bond, in which two ions of opposing charge are attracted to each other. Thus, ionic interactions between particles are another type of intermolecular interaction. Substances that contain ionic interactions are relatively strongly held together, so these substances typically have high melting and boiling points. Sodium chloride (Figure \(\PageIndex{3}\)) is an example of a substance whose particles experience ionic interactions (Table \(\PageIndex{1}\)). These attractive forces are sometimes referred to as ion-ion interactions.
Covalent Molecular Compounds
There are two different covalent structures: molecular and network. Covalent network compounds like SiO2 (quartz) have structures of atoms in a network like diamond described earlier. In this section, we are dealing with the molecular type that contains individual molecules. The bonding between atoms in the individual molecule is covalent but the attractive forces between the molecules are called intermolecular forces (IMF).
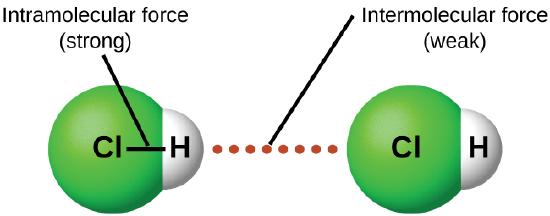
In contrast to intramolecular forces (see Figure 8.1.4), such as the covalent bonds that hold atoms together in molecules and polyatomic ions, intermolecular forces hold molecules together in a liquid or solid. Intermolecular forces are generally much weaker than covalent bonds. For example, it requires 927 kJ to overcome the intramolecular forces and break both O–H bonds in 1 mol of water, but it takes only about 41 kJ to overcome the intermolecular attractions and convert 1 mol of liquid water to water vapor at 100°C. (Despite this seemingly low value, the intermolecular forces in liquid water are among the strongest such forces known!) Given the large difference in the strengths of intra- and intermolecular forces, changes between the solid, liquid, and gaseous states almost invariably occur for molecular substances without breaking covalent bonds.
In this section, we will discuss the three types of IMF in molecular compounds: dipole-dipole, hydrogen bonding and London dispersion forces.
Dipole-dipole Intermolecular Forces
As discussed in Section 4.4, covalent bond that has an unequal sharing of electrons is called a polar covalent bond. (A covalent bond that has an equal sharing of electrons, as in a covalent bond with the same atom on each side, is called a nonpolar covalent bond.) A molecule with a net unequal distribution of electrons in its covalent bonds is a polar molecule. HF is an example of a polar molecule (see Figure 8.1.5).

The charge separation in a polar covalent bond is not as extreme as is found in ionic compounds, but there is a related result: oppositely charged ends of different molecules will attract each other. This type of intermolecular interaction is called a dipole-dipole interaction. Many molecules with polar covalent bonds experience dipole-dipole interactions.
The covalent bonds in some molecules are oriented in space in such a way that the bonds in the molecules cancel each other out. The individual bonds are polar, but due to molecular symmetry, the overall molecule is not polar; rather, the molecule is nonpolar. Such molecules experience little or no dipole-dipole interactions. Carbon dioxide (CO2) and carbon tetrachloride (CCl4) are examples of such molecules (Figure \(\PageIndex{6}\)).
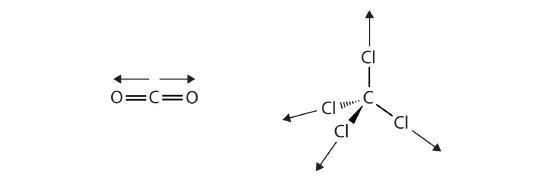
Recall from the Sections 4.4 and 4.5, on chemical bonding and molecular geometry that polar molecules have a partial positive charge on one side and a partial negative charge on the other side of the molecule—a separation of charge called a dipole. Consider a polar molecule such as hydrogen chloride, HCl. In the HCl molecule, the more electronegative Cl atom bears the partial negative charge, whereas the less electronegative H atom bears the partial positive charge. An attractive force between HCl molecules results from the attraction between the positive end of one HCl molecule and the negative end of another. This attractive force is called a dipole-dipole attraction—the electrostatic force between the partially positive end of one polar molecule and the partially negative end of another, as illustrated in Figure \(\PageIndex{7}\).

The effect of a dipole-dipole attraction is apparent when we compare the properties of HCl molecules to nonpolar F2 molecules. Both HCl and F2 consist of the same number of atoms and have approximately the same molecular mass. At a temperature of 150 K, molecules of both substances would have the same average kinetic energy. However, the dipole-dipole attractions between HCl molecules are sufficient to cause them to “stick together” to form a liquid, whereas the relatively weaker dispersion forces between nonpolar F2 molecules are not, and so this substance is gaseous at this temperature. The higher normal boiling point of HCl (188 K) compared to F2 (85 K) is a reflection of the greater strength of dipole-dipole attractions between HCl molecules, compared to the attractions between nonpolar F2 molecules. We will often use values such as boiling or freezing points as indicators of the relative strengths of IMFs of attraction present within different substances.
Example \(\PageIndex{1}\)
Predict which will have the higher boiling point: N2 or CO. Explain your reasoning.
Solution
CO and N2 are both diatomic molecules with masses of about 28 amu, so they experience similar London dispersion forces. Because CO is a polar molecule, it experiences dipole-dipole attractions. Because N2 is nonpolar, its molecules cannot exhibit dipole-dipole attractions. The dipole-dipole attractions between CO molecules are comparably stronger than the dispersion forces between nonpolar N2 molecules, so CO is expected to have the higher boiling point.
Exercise \(\PageIndex{1}\)
Predict which will have the higher boiling point: \(\ce{ICl}\) or \(\ce{Br2}\). Explain your reasoning.
- Answer
-
ICl. ICl and Br2 have similar masses (~160 amu) and therefore experience similar London dispersion forces. ICl is polar and thus also exhibits dipole-dipole attractions; Br2 is nonpolar and does not. The relatively stronger dipole-dipole attractions require more energy to overcome, so ICl will have the higher boiling point.
Hydrogen Bonding Intermolecular Forces
Molecules with hydrogen atoms bonded to electronegative atoms such as O, N, and F tend to exhibit unusually strong intermolecular interactions due to a particularly strong type of dipole-dipole attraction called hydrogen bonding. The very large difference in electronegativity between the H atom (2.1) and the atom to which it is bonded (4.0 for an F atom, 3.5 for an O atom, or 3.0 for a N atom), combined with the very small size of a H atom and the relatively small sizes of F, O, or N atoms, leads to highly concentrated partial charges with these atoms. Because the hydrogen atom does not have any electrons other than the ones in the covalent bond, its positively charged nucleus is almost completely exposed, allowing strong attractions to other nearby lone pairs of electrons.
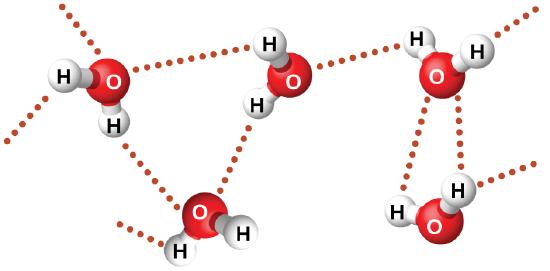
Examples of hydrogen bonds include HF⋯HF, H2O⋯HOH, and H3N⋯HNH2, in which the hydrogen bonds are denoted by dots. Figure \(\PageIndex{8}\) illustrates hydrogen bonding between water molecules. The physical properties of water, which has two O–H bonds, are strongly affected by the presence of hydrogen bonding between water molecules. Most molecular compounds that have a mass similar to water are gases at room temperature. However, because of the strong hydrogen bonds, water molecules are able to stay condensed in the liquid state.
A hydrogen bond is an intermolecular attractive force in which a hydrogen atom, that is covalently bonded to a small, highly electronegative atom, is attracted to a lone pair of electrons on an atom in a neighboring molecule. Figure \(\PageIndex{9}\) shows how methanol (CH3OH) molecules experience hydrogen bonding. Methanol contains both a hydrogen atom attached to O; methanol can thus form hydrogen bonds by acting as either a hydrogen bond donor or a hydrogen bond acceptor (lone pair). The hydrogen-bonded structure of methanol is as follows:
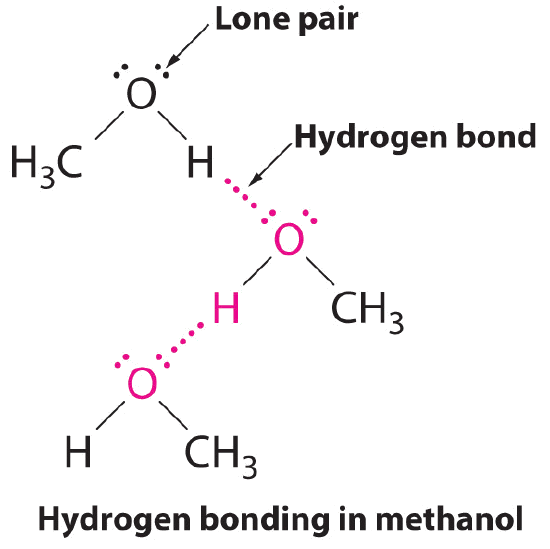
Despite use of the word “bond,” keep in mind that hydrogen bonds are intermolecular attractive forces, not intramolecular attractive forces (covalent bonds). Hydrogen bonds are much weaker than covalent bonds, but are generally much stronger than other dipole-dipole attractions and dispersion forces.
Effect of Hydrogen Bonding on Boiling Points
Consider the compounds dimethylether (CH3OCH3), ethanol (CH3CH2OH), and propane (CH3CH2CH3). Their boiling points, not necessarily in order, are −42.1 °C, −24.8 °C, and 78.4 °C. Match each compound with its boiling point. Explain your reasoning.
Solution
The shapes of CH3OCH3, CH3CH2OH, and CH3CH2CH3 are similar, as are their molar masses (46 g/mol, 46 g/mol, and 44 g/mol, respectively), so they will exhibit similar dispersion forces. Since CH3CH2CH3 is nonpolar, it may exhibit only dispersion forces. Because CH3OCH3 is polar, it will also experience dipole-dipole attractions. Finally, CH3CH2OH has an −OH group, and so it will experience the uniquely strong dipole-dipole attraction known as hydrogen bonding. So the ordering in terms of strength of IMFs, and thus boiling points, is CH3CH2CH3 < CH3OCH3 < CH3CH2OH. The boiling point of propane is −42.1 °C, the boiling point of dimethylether is −24.8 °C, and the boiling point of ethanol is 78.5 °C.
Exercise \(\PageIndex{2}\)
Ethane (CH3CH3) has a melting point of −183 °C and a boiling point of −89 °C. Predict the melting and boiling points for methylamine (CH3NH2). Explain your reasoning.
- Answer
-
The melting point and boiling point for methylamine are predicted to be significantly greater than those of ethane. CH3CH3 and CH3NH2 are similar in size and mass, but methylamine possesses an −NH group and therefore may exhibit hydrogen bonding. This greatly increases its IMFs, and therefore its melting and boiling points. It is difficult to predict values, but the known values are a melting point of −93 °C and a boiling point of −6 °C.
Hydrogen Bonding and DNA
Deoxyribonucleic acid (DNA) is found in every living organism and contains the genetic information that determines the organism’s characteristics, provides the blueprint for making the proteins necessary for life, and serves as a template to pass this information on to the organism’s offspring. A DNA molecule consists of two (anti-)parallel chains of repeating nucleotides, which form its well-known double helical structure, as shown in Figure \(\PageIndex{10}\).
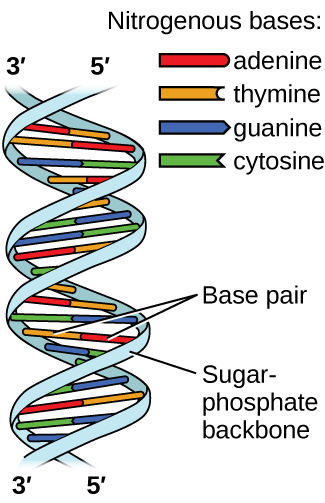
Each nucleotide contains a (deoxyribose) sugar bound to a phosphate group on one side, and one of four nitrogenous bases on the other. Two of the bases, cytosine (C) and thymine (T), are single-ringed structures known as pyrimidines. The other two, adenine (A) and guanine (G), are double-ringed structures called purines. These bases form complementary base pairs consisting of one purine and one pyrimidine, with adenine pairing with thymine, and cytosine with guanine. Each base pair is held together by hydrogen bonding. A and T share two hydrogen bonds, C and G share three, and both pairings have a similar shape and structure Figure \(\PageIndex{11}\)
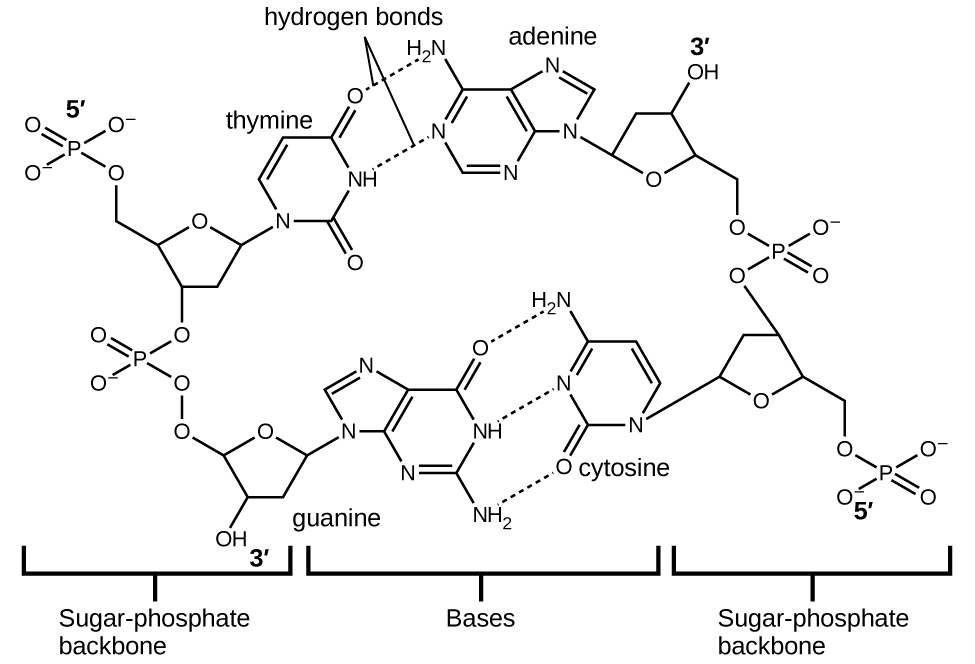
The cumulative effect of millions of hydrogen bonds effectively holds the two strands of DNA together. Importantly, the two strands of DNA can relatively easily “unzip” down the middle since hydrogen bonds are relatively weak compared to the covalent bonds that hold the atoms of the individual DNA molecules together. This allows both strands to function as a template for replication.
London Dispersion Forces
Finally, there are forces between all molecules that are caused by electrons being in different places in a molecule at any one time, which sets up a temporary separation of charge that disappears almost as soon as it appears. These are very weak intermolecular interactions and are called dispersion forces (or London forces). (An alternate name is London dispersion forces.) Molecules that experience no other type of intermolecular interaction will at least experience dispersion forces. Substances that experience only dispersion forces are typically soft in the solid phase and have relatively low melting points. Examples include waxes, which are long hydrocarbon chains that are solids at room temperature because the molecules have so many electrons. The resulting dispersion forces between these molecules make them assume the solid phase at normal temperatures.
Dispersion forces that develop between atoms in different molecules can attract the two molecules to each other. The forces are relatively weak, however, and become significant only when the molecules are very close. Larger and heavier atoms and molecules exhibit stronger dispersion forces than do smaller and lighter atoms and molecules. F2 and Cl2 are gases at room temperature (reflecting weaker attractive forces); Br2 is a liquid, and I2 is a solid (reflecting stronger attractive forces). Trends in observed melting and boiling points for the halogens clearly demonstrate this effect, as seen in Table 8.1.2.
| Halogen | Molar Mass | Atomic Radius | Melting Point | Boiling Point |
|---|---|---|---|---|
| fluorine, F2 | 38 g/mol | 72 pm | 53 K | 85 K |
| chlorine, Cl2 | 71 g/mol | 99 pm | 172 K | 238 K |
| bromine, Br2 | 160 g/mol | 114 pm | 266 K | 332 K |
| iodine, I2 | 254 g/mol | 133 pm | 387 K | 457 K |
| astatine, At2 | 420 g/mol | 150 pm | 575 K | 610 K |
The increase in melting and boiling points with increasing atomic/molecular size may be rationalized by considering how the strength of dispersion forces is affected by the electronic structure of the atoms or molecules in the substance. In a larger atom, the valence electrons are, on average, farther from the nuclei than in a smaller atom. Thus, they are less tightly held and can more easily form the temporary dipoles that produce the attraction. The measure of how easy or difficult it is for another electrostatic charge (for example, a nearby ion or polar molecule) to distort a molecule’s charge distribution (its electron cloud) is known as polarizability. A molecule that has a charge cloud that is easily distorted is said to be very polarizable and will have large dispersion forces; one with a charge cloud that is difficult to distort is not very polarizable and will have small dispersion forces.
Example \(\PageIndex{3}\)
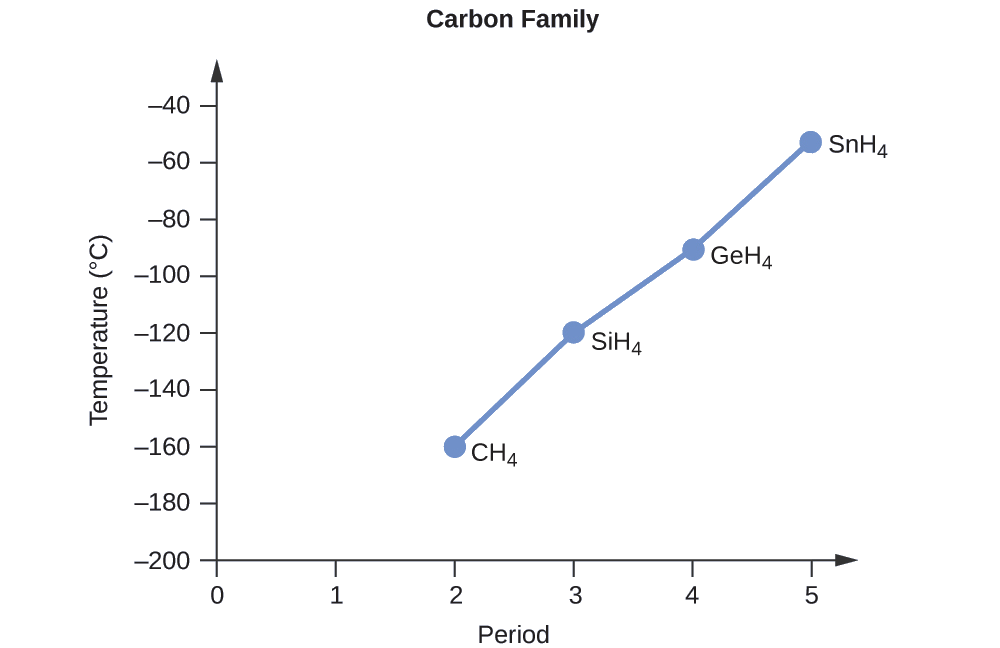
Order the following compounds of a group 14 element and hydrogen from lowest to highest boiling point: CH4, SiH4, GeH4, and SnH4. Explain your reasoning.
Solution
Applying the skills acquired in the chapter on chemical bonding and molecular geometry, all of these compounds are predicted to be nonpolar, so they may experience only dispersion forces: the smaller the molecule, the less polarizable and the weaker the dispersion forces; the larger the molecule, the larger the dispersion forces. The molar masses of CH4, SiH4, GeH4, and SnH4 are approximately 16 g/mol, 32 g/mol, 77 g/mol, and 123 g/mol, respectively. Therefore, CH4 is expected to have the lowest boiling point and SnH4 the highest boiling point. The ordering from lowest to highest boiling point is expected to be
CH4 < SiH4 < GeH4 < SnH4
A graph of the actual boiling points of these compounds versus the period of the group 14 elementsshows this prediction to be correct:
Exercise \(\PageIndex{3}\)
Order the following hydrocarbons from lowest to highest boiling point: C2H6, C3H8, and C4H10.
- Answer
-
All of these compounds are nonpolar and only have London dispersion forces: the larger the molecule, the larger the dispersion forces and the higher the boiling point. The ordering from lowest to highest boiling point is therefore
C2H6 < C3H8 < C4H10.
Applications: Geckos and Intermolecular Forces
Geckos have an amazing ability to adhere to most surfaces. They can quickly run up smooth walls and across ceilings that have no toe-holds, and they do this without having suction cups or a sticky substance on their toes. And while a gecko can lift its feet easily as it walks along a surface, if you attempt to pick it up, it sticks to the surface. How are geckos (as well as spiders and some other insects) able to do this? Although this phenomenon has been investigated for hundreds of years, scientists only recently uncovered the details of the process that allows geckos’ feet to behave this way.

Geckos’ toes are covered with hundreds of thousands of tiny hairs known as setae, with each seta, in turn, branching into hundreds of tiny, flat, triangular tips called spatulae. The huge numbers of spatulae on its setae provide a gecko, shown in Figure 8.1.12, with a large total surface area for sticking to a surface. In 2000, Kellar Autumn, who leads a multi-institutional gecko research team, found that geckos adhered equally well to both polar silicon dioxide and nonpolar gallium arsenide. This proved that geckos stick to surfaces because of dispersion forces—weak intermolecular attractions arising from temporary, synchronized charge distributions between adjacent molecules. Although dispersion forces are very weak, the total attraction over millions of spatulae is large enough to support many times the gecko’s weight.
In 2014, two scientists developed a model to explain how geckos can rapidly transition from “sticky” to “non-sticky.” Alex Greaney and Congcong Hu at Oregon State University described how geckos can achieve this by changing the angle between their spatulae and the surface. Geckos’ feet, which are normally nonsticky, become sticky when a small shear force is applied. By curling and uncurling their toes, geckos can alternate between sticking and unsticking from a surface, and thus easily move across it. Further investigations may eventually lead to the development of better adhesives and other applications.
Boiling Points and Bonding Types
In order for a substance to enter the gas phase, its particles must completely overcome the intermolecular forces holding them together. Therefore, a comparison of boiling points is essentially equivalent to comparing the strengths of the attractive intermolecular forces exhibited by the individual molecules. For small molecular compounds, London dispersion forces are the weakest intermolecular forces. Dipole-dipole forces are somewhat stronger, and hydrogen bonding is a particularly strong form of dipole-dipole interaction. However, when the mass of a nonpolar molecule is sufficiently large, its dispersion forces can be stronger than the dipole-dipole forces in a lighter polar molecule. Thus, nonpolar Cl2 has a higher boiling point than polar HCl.
| Substance | Strongest Intermolecular Force | Boiling Point \(\left( ^\text{o} \text{C} \right)\) |
|---|---|---|
| \(\ce{H_2}\) | dispersion | -253 |
| \(\ce{Ne}\) | dispersion | -246 |
| \(\ce{O_2}\) | dispersion | -183 |
| \(\ce{Cl_2}\) | dispersion | -34 |
| \(\ce{HCl}\) | dipole-dipole | -85 |
| \(\ce{HBr}\) | dipole-dipole | -66 |
| \(\ce{H_2S}\) | dipole-dipole | -61 |
| \(\ce{NH_3}\) | hydrogen bonding | -33 |
| \(\ce{HF}\) | hydrogen bonding | 20 |
| \(\ce{H_2O}\) | hydrogen bonding | 100 |
Example \(\PageIndex{4}\): Intermolecular Forces
What intermolecular forces besides dispersion forces, if any, exist in each substance? Are any of these substances solids at room temperature?
- potassium chloride (KCl)
- ethanol (C2H5OH)
- bromine (Br2)
Solution
- Potassium chloride is composed of ions, so the intermolecular interaction in potassium chloride is ionic forces. Because ionic interactions are strong, it might be expected that potassium chloride is a solid at room temperature.
- Ethanol has a hydrogen atom attached to an oxygen atom, so it would experience hydrogen bonding. If the hydrogen bonding is strong enough, ethanol might be a solid at room temperature, but it is difficult to know for certain. (Ethanol is actually a liquid at room temperature.)
- Elemental bromine has two bromine atoms covalently bonded to each other. Because the atoms on either side of the covalent bond are the same, the electrons in the covalent bond are shared equally, and the bond is a nonpolar covalent bond. Thus, diatomic bromine does not have any intermolecular forces other than dispersion forces. It is unlikely to be a solid at room temperature unless the dispersion forces are strong enough. Bromine is a liquid at room temperature.
Exercise \(\PageIndex{4}\)
What intermolecular forces besides dispersion forces, if any, exist in each substance? Are any of these substances solids at room temperature?
- methylamine (CH3NH2)
- calcium sulfate (CaSO4)
- carbon monoxide (CO)
- Answer
-
a. dipole-dipole, hydrogen bonding
b. ionic forces (solid at room temperature)
c. dipole-dipole
Key Takeaways
- A phase is a form of matter that has the same physical properties throughout.
- Molecules interact with each other through various forces: dipole-dipole interactions, hydrogen bonding, and dispersion forces.
- Dipole-dipole attractions result from the electrostatic attraction of the partial negative end of one dipolar molecule for the partial positive end of another.
- Hydrogen bonds are a special type of dipole-dipole attraction that results when hydrogen is bonded to one of the three most electronegative elements: F, O, or N.
- The temporary dipole that results from the motion of the electrons in an atom can induce a dipole in an adjacent atom and give rise to the London dispersion force. London forces increase with increasing molecular size.

