23.2: Pyrometallurgy
- Page ID
- 91359
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Identify natural sources of representative metals
- Describe chemical reduction processes used to prepare these elements from natural sources
It is possible to isolate many of the representative metals by chemical reduction using other elements as reducing agents. In general, chemical reduction is much less expensive than electrolysis, and for this reason, chemical reduction is the method of choice for the isolation of these elements. For example, it is possible to produce potassium, rubidium, and cesium by chemical reduction, as it is possible to reduce the molten chlorides of these metals with sodium metal. This may be surprising given that these metals are more reactive than sodium; however, the metals formed are more volatile than sodium and can be distilled for collection. The removal of the metal vapor leads to a shift in the equilibrium to produce more metal (via the Le Chatelier’s principle). The production of magnesium, zinc, and tin provide additional examples of chemical reduction.
Thermodynamics of Pyrometallurgy
The oldest, and still the most common smelting process for oxide ores involves heating them in the presence of carbon. Originally, charcoal was used, but industrial-scale smelting uses coke, a crude form of carbon prepared by pyrolysis (heating) of coal. The basic reactions are:
\[\ce{MO + C \rightleftharpoons M + CO }\label{2.1}\]
\[\ce{MO + 1/2 O_2 \rightleftharpoons M + 1/2 CO2} \label{2.2}\]
\[\ce{MO + CO \rightleftharpoons M + CO2 }\label{2.3}\]
Each of these can be regarded as a pair of coupled reactions in which the metal M and the carbon are effectively competing for the oxygen atom. Using reaction \(\ref{2.1}\) as an example, it can be broken down into the following two parts:
\[\ce{MO \rightleftharpoons M + 1/2 O2 } \;\;\; ΔG^o > 0 \label{2.4}\]
\[\ce{C + 1/2 O_2 \rightleftharpoons CO } \;\;\; ΔG^o < 0 \label{2.5}\]
At ordinary environmental temperatures, reaction \(\ref{2.4}\) is always spontaneous in the reverse direction (that is why ores form in the first place!), so \(ΔG°\) of Reaction \(\ref{2.4}\) will be positive. \(ΔG°\) for reaction \(\ref{2.5}\) is always negative, but at low temperatures it will not be sufficiently negative to drive \(\ref{2.4}\).

The smelting process depends on the different ways in which the free energies of reactions like \(\ref{2.4}\) and \(\ref{2.4}\) vary with the temperature. This temperature dependence is almost entirely dominated by the \(TΔS°\) term in the Gibbs function (Equation \ref{Gibbs}), and thus by the entropy change.
\[ΔG° = ΔH° - TΔS° \label{Gibbs}\]
The latter depends mainly on \(Δn_g\), the change in the number of moles of gas in the reaction. Removal of oxygen from the ore is always accompanied by a large increase in the system volume so \(ΔS\) for this step is always positive and the reaction becomes more spontaneous at higher temperatures. The temperature dependences of the reactions that take up oxygen vary, however (Table \(\PageIndex{1}\)).
|
Reaction
|
Δng
|
d(ΔG°)/dT
|
|---|---|---|
| \(\ce{C + 1/2 O2 → CO}\) |
0.5
|
<0
|
| \(\ce{C + O2 → CO2}\) |
0
|
0
|
| \(\ce{CO + 1/2 O2 →CO2}\) |
–0.5
|
>0
|
A plot of the temperature dependences of the free energies of these reactions, superimposed on similar plots for the oxygen removal reactions \(\ref{2.4}\) is called an Ellingham diagram (Figure \(\PageIndex{2}\)). For a given oxide MO to be smeltable, the temperature must be high enough that reaction \(\ref{2.4}\) falls below that of at least one of the oxygen-consuming reactions. The slopes of the lines on this diagram are determined by the sign of the entropy change.
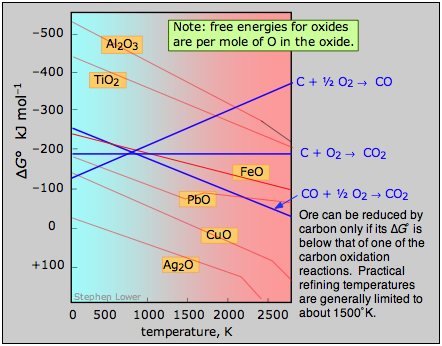
Figure \(\PageIndex{2}\): Ellingham diagram. An ore can be reduced by carbon only if its Gibbs free energy of formation falls below that of one of the carbon reduction reactions (blue lines.) Practical refining temperatures are generally limited to about 1500°K.
Examination of the Ellingham diagram shown in Figure \(\PageIndex{2}\) illustrates why the metals known to the ancients were mainly those such as copper and lead, which can be obtained by smelting at the relatively low temperatures that were obtainable by the methods available at the time in which a charcoal fire supplied both the heat and the carbon. Thus the bronze age preceded the iron age; the latter had to await the development of technology capable of producing higher temperatures, such as the blast furnace. Smelting of aluminum oxide by carbon requires temperatures too high to be practical; commercial production of aluminum is accomplished by electrolysis of the molten ore.
In pyrometallurgy, an ore is heated with a reductant to obtain the metal. Theoretically, it should be possible to obtain virtually any metal from its ore by using coke as the reductant. For example, the reduction of calcium metal from \(CaO_{(s)}\):
\[\mathrm{CaO(s) + C(s)\xrightarrow{\Delta}Ca(l) + CO(g)} \label{23.2.1}\]
Unfortunately, many transition metals (e.g., Titanium) react with carbon to form stable binary carbides:
\[\ce{Ti + C \rightarrow TiC}.\]
Consequently, more expensive reductants (such as hydrogen, aluminum, magnesium, or calcium) must be used to obtain these metals. Many metals that occur naturally as sulfides can be obtained by heating the sulfide in air, as shown for lead in the following equation:
\[\ce {PbS(s) + O_2(g) \xrightarrow{\Delta}Pb(l) + SO_2(g)} \label{23.2.2}\]
The reaction is driven to completion by the formation of \(SO_2\), a stable gas.
Pyrometallurgy in the Extraction of Iron
Pyrometallurgy is also used in the iron and steel industries. The overall reaction for the production of iron in a blast furnace is as follows (via \(\ref{2.1}\)):
\[\mathrm{Fe_2O_3(s) +3C(s)\xrightarrow{\Delta}2Fe(l) +3CO(g)} \label{23.2.3}\]
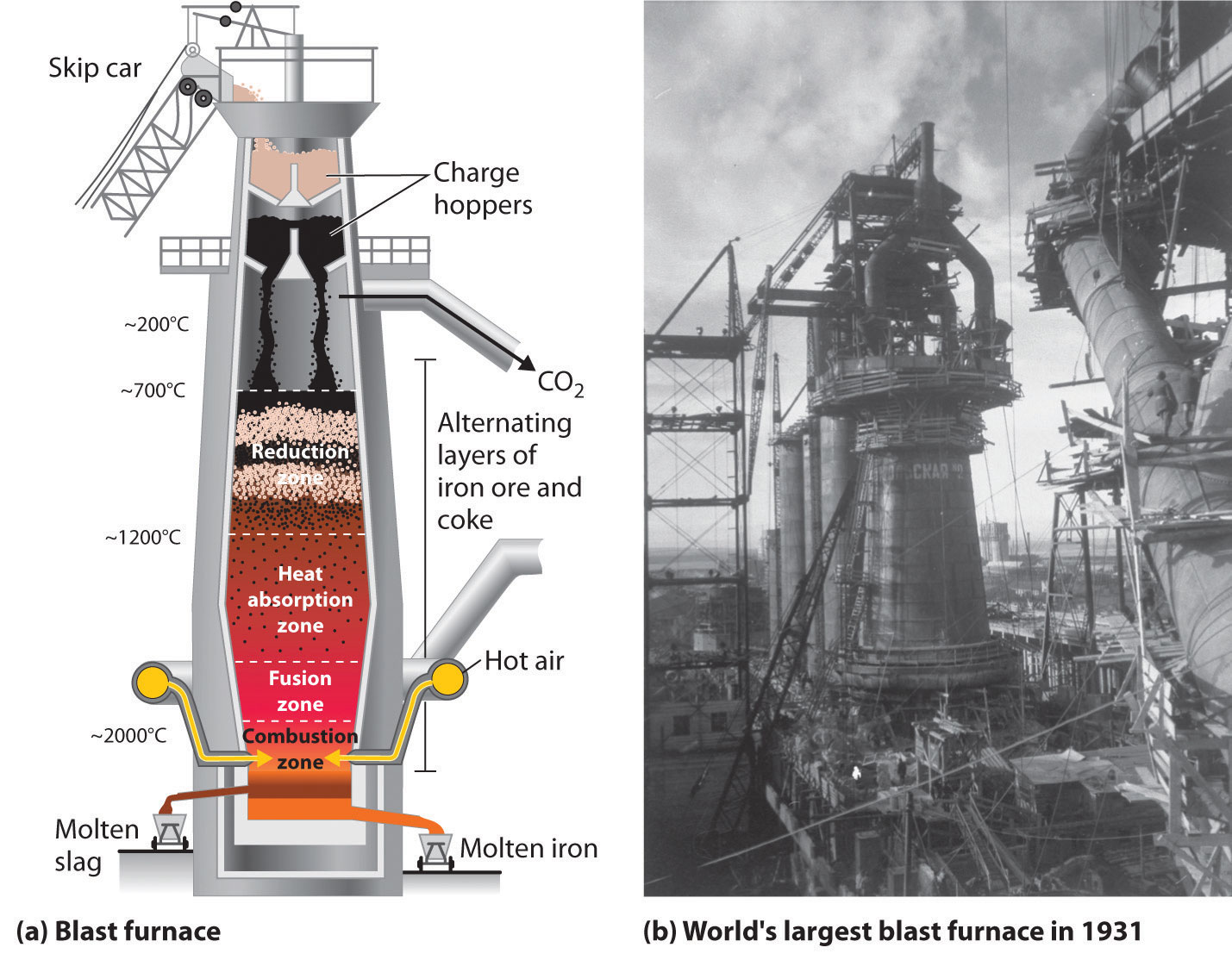
The actual reductant is CO, which reduces Fe2O3 to give Fe(l) and CO2(g) (Equation \(\ref{2.3}\)); the CO2 is then reduced back to CO by reaction with excess carbon. As the ore, lime, and coke drop into the furnace (Figure \(\PageIndex{3}\)), any silicate minerals in the ore react with the lime to produce a low-melting mixture of calcium silicates called slag, which floats on top of the molten iron. Molten iron is then allowed to run out the bottom of the furnace, leaving the slag behind. Originally, the iron was collected in pools called pigs, which is the origin of the name pig iron.
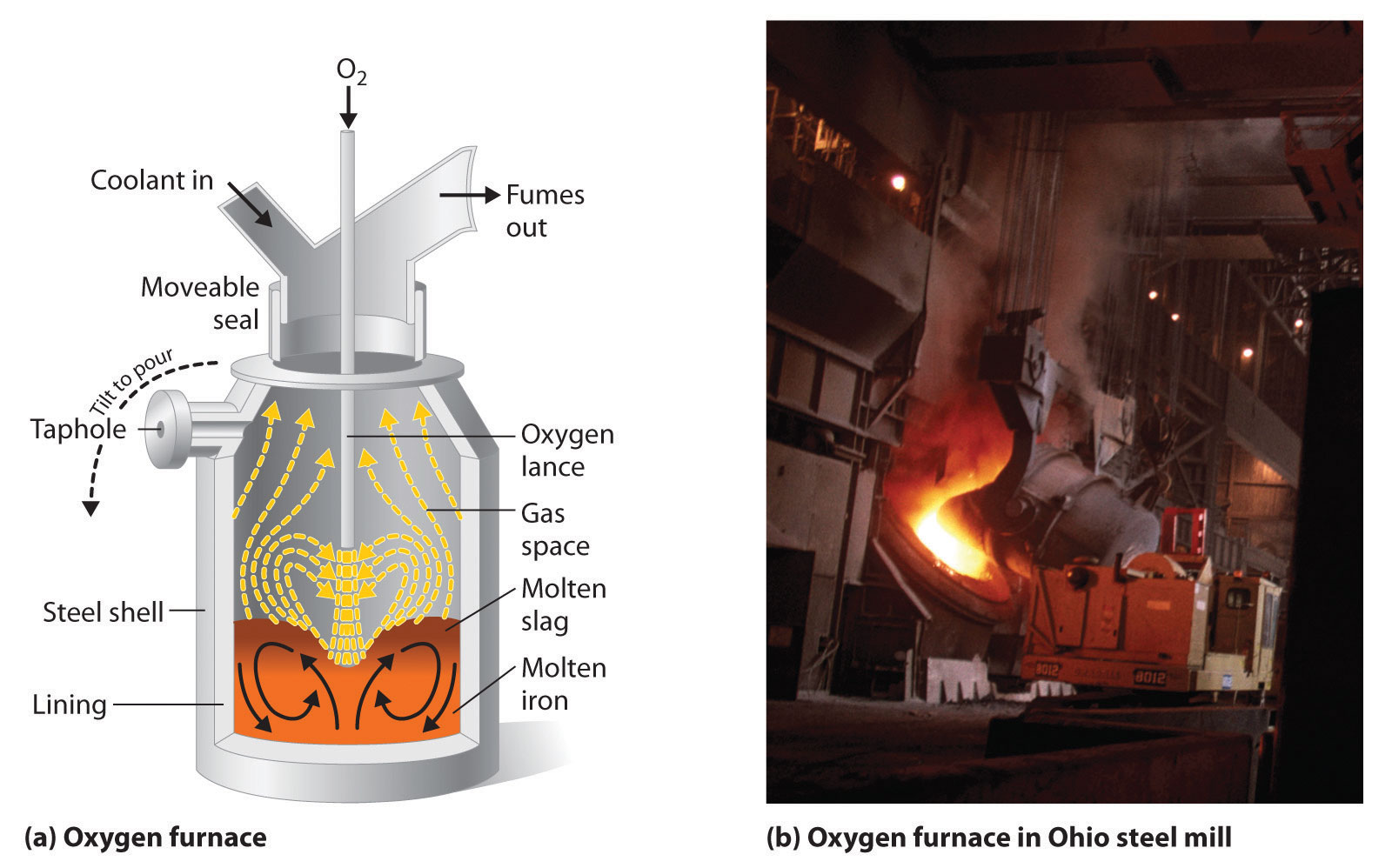
Iron that is obtained directly from a blast furnace has an undesirably low melting point (about 1100 °C instead of 1539 °C) because it contains a large amount of dissolved carbon. It contains other impurities (such as Si, S, P, and Mn from contaminants in the iron ore that were also reduced during processing) that must be removed because they make iron brittle and unsuitable for most structural applications. In the Bessemer process, oxygen is blown through the molten pig iron to remove the impurities by selective oxidation because these impurities are more readily oxidized than iron (Figure \(\PageIndex{4}\)). In the final stage of this process, small amounts of other metals are added at specific temperatures to produce steel with the desired combination of properties.
Pyrometallurgy in the Extraction of Magnesium
The Pidgeon process is one of the methods of magnesium metal production via a high temperature (800-1400°C) process with silicon as the reducing agent (instead of carbon for iron extraction). The Pidgeon process involves the reaction of magnesium oxide with elemental silicon at high temperatures to form pure magnesium:
\[\ce{Si}(s)+\ce{2MgO}(s)\xrightarrow{Δ}\ce{SiO2}(s)+\ce{2Mg}(g)\]
Although this reaction is unfavorable in terms of thermodynamics, the removal of the magnesium vapor produced takes advantage of Le Chatelier’s principle to continue the forward progress of the reaction. Over 75% of the world’s production of magnesium, primarily in China, comes from this process.


The usual metallurgic use of carbon as the reducing agent instead of silicon cannot be used, because the silicon dioxide is a solid, while carbon dioxide and monoxide are both gaseous, and would follow the magnesium into the condensing zone, reverting the reaction as follows.
\[\ce{C (s) + MgO (s) \rightleftharpoons CO(g) + Mg (g) }\]
\[\ce{CO (g) + Mg (g) \rightleftharpoons C(s) + MgO (s) }\]
Hence, reducing with carbon would produce no yield when the vapors moved into the cooler condensing zones inside the reactor, even though temporarily there would be intermediate carbon monoxide and actual magnesium vapors.
Pyrometallurgy in the Extraction of Zinc
Zinc smelting is the process of converting zinc ores into pure zinc. Zinc smelting has historically been more difficult than the smelting of other metals, e.g. iron, because in contrast, zinc has a low boiling point. There are two methods of smelting zinc: the pyrometallurgical process and the electrolysis process; both methods are still used. Both of these processes share the same first step: roasting.
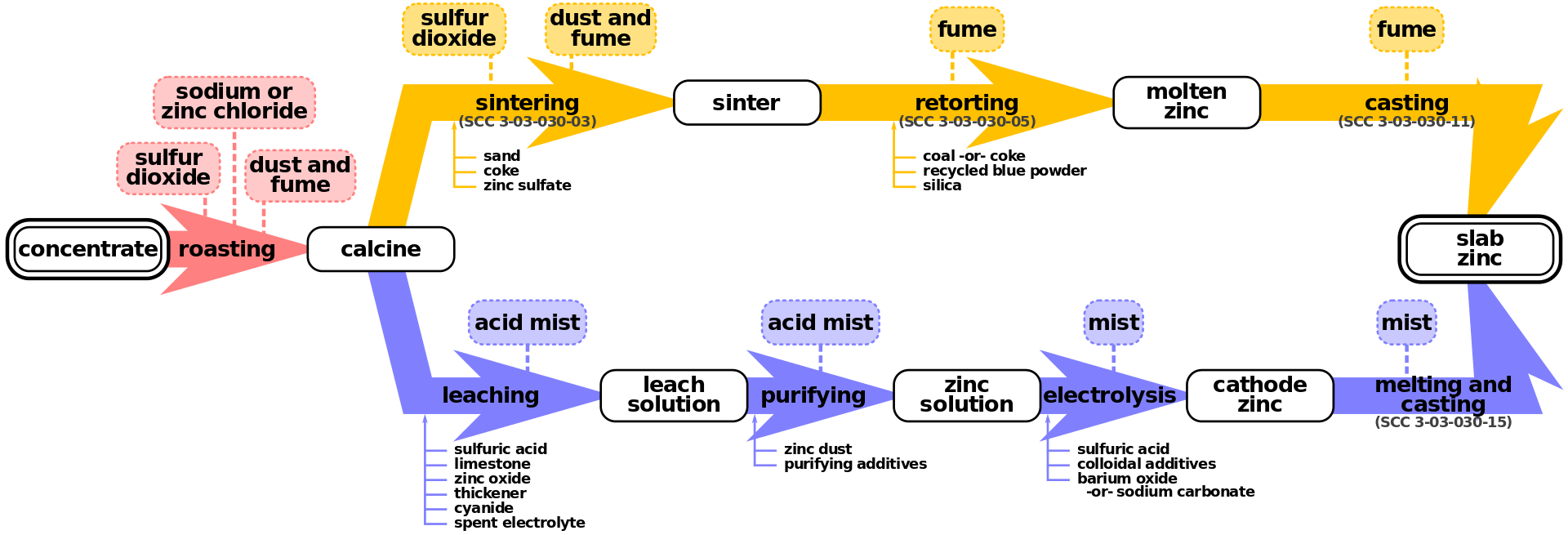
Zinc ores usually contain zinc sulfide, zinc oxide, or zinc carbonate. After separation of these compounds from the ores, heating in air converts the ore to zinc oxide by one of the following reactions:
\[\ce{2ZnS}(s)+\ce{3O2}(g)\xrightarrow{Δ}\ce{2ZnO}(s)+\ce{2SO2}(g)\]
\[\ce{ZnCO3}(s)\xrightarrow{Δ}\ce{ZnO}(s)+\ce{Co2}(g)\]
Carbon, in the form of coal, reduces the zinc oxide to form zinc vapor:
\[\ce{ZnO}(s)+\ce{C}(s)⟶\ce{Zn}(g)+\ce{CO}(g)\]
The zinc can be distilled (boiling point 907 °C) and condensed. This zinc contains impurities of cadmium (767 °C), iron (2862 °C), lead (1750 °C), and arsenic (613 °C). Careful redistillation produces pure zinc. Arsenic and cadmium are distilled from the zinc because they have lower boiling points. At higher temperatures, the zinc is distilled from the other impurities, mainly lead and iron.
Contributors and Attributions
- Wikipedia
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

