21.8: Nuclear Fusion

Learning Objectives

• Describe the nuclear reactions in a nuclear fusion reaction
• Quantify the energy released or absorbed in a fusion reaction

The process of converting very light nuclei into heavier nuclei is also accompanied by the conversion of mass into large amounts of energy, a process called fusion. The principal source of energy in the sun is a net fusion reaction in which four hydrogen nuclei fuse and produce one helium nucleus and two positrons. This is a net reaction of a more complicated series of events:

\[\ce{4^1_1H ⟶ ^4_2He + 2^0_{+1}n}\]

A helium nucleus has a mass that is 0.7% less than that of four hydrogen nuclei; this lost mass is converted into energy during the fusion. This reaction produces about 3.6 × 10¹¹ kJ of energy per mole of \(\ce{^4_2He}\) produced. This is somewhat larger than the energy produced by the nuclear fission of one mole of U-235 (1.8 × 10¹⁰ kJ), and over 3 million times larger than the energy produced by the (chemical) combustion of one mole of octane (5471 kJ).

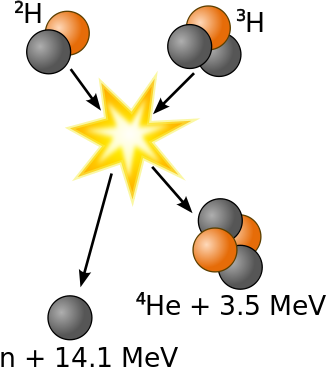
It has been determined that the nuclei of the heavy isotopes of hydrogen, a deuteron, \(^2_1H\) and a triton, \(^3_1H\), undergo fusion at extremely high temperatures (thermonuclear fusion). They form a helium nucleus and a neutron:

\[\ce{^2_1H + ^3_1H ⟶ ^4_2He + 2^1_0n}\]

This change proceeds with a mass loss of 0.0188 amu, corresponding to the release of 1.69 × 10⁹ kilojoules per mole of \(\ce{^4_2He}\) formed. The very high temperature is necessary to give the nuclei enough kinetic energy to overcome the very strong repulsive forces resulting from the positive charges on their nuclei so they can collide.

Figure \(\PageIndex{1}\): Fusion of deuterium with tritium creating helium-4, freeing a neutron, and releasing 17.59 MeV of energy, as an appropriate amount of mass changing forms to appear as the kinetic energy of the products, in agreement with kinetic \(E = Δmc^2\), where Δm is the change in rest mass of particles.[Image use with permission via Wikipedia (Wykis)

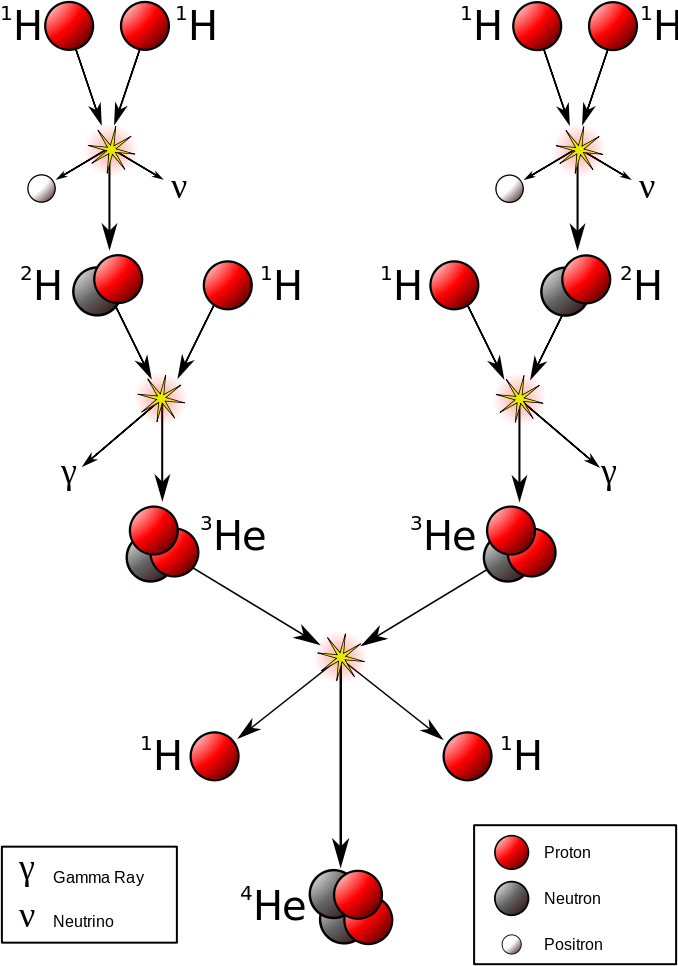
The most important fusion process in nature is the one that powers stars. In the 20th century, it was realized that the energy released from nuclear fusion reactions accounted for the longevity of the Sun and other stars as a source of heat and light. The fusion of nuclei in a star, starting from its initial hydrogen and helium abundance, provides that energy and synthesizes new nuclei as a byproduct of that fusion process. The prime energy producer in the Sun is the fusion of hydrogen to form helium, which occurs at a solar-core temperature of 14 million kelvin. The net result is the fusion of four protons into one alpha particle, with the release of two positrons, two neutrinos (which changes two of the protons into neutrons), and energy (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): (left) The Sun is a main-sequence star, and thus generates its energy by nuclear fusion of hydrogen nuclei into helium. In its core, the Sun fuses 620 million metric tons of hydrogen each second. (right) The proton-proton chain dominates in stars the size of the Sun or smaller.

Example \(\PageIndex{1}\)

Calculate the energy released in each of the following hypothetical processes.

1. \(\ce{3 ^4_2He \rightarrow ^{12}_6C}\)
2. \(\ce{6 ^1_1H + 6 ^1_0n \rightarrow ^{12}_6C}\)
3. \(\ce{6 ^2_1D \rightarrow ^{12}_6C}\)

Solution

1. \(Q_a = 3 \times 4.0026 - 12.000) \,amu \times (1.4924\times 10^{-10} \,J/amu) = 1.17 \times 10^{-12} \,J\)
2. \(Q_b = (6 \times (1.007825 + 1.008665) - 12.00000)\, amu \times (1.4924\times 10^{1-0} J/amu) = 1.476\times 10^{-11} \,J\)
3. \(Q_c = 6 \times 2.014102 - 12.00000 \, amu \times (1.4924\times 10^{-10} \, J/amu) = 1.263\times 10^{-11}\, J\)

Fusion of \(\ce{He}\) to give \(\ce{C}\) releases the least amount of energy, because the fusion to produce He has released a large amount. The difference between the second and the third is the binding energy of deuterium. The conservation of mass-and-energy is well illustrated in these calculations. On the other hand, the calculation is based on the conservation of mass-and-energy.

Nuclear Reactors

Useful fusion reactions require very high temperatures for their initiation—about 15,000,000 K or more. At these temperatures, all molecules dissociate into atoms, and the atoms ionize, forming plasma. These conditions occur in an extremely large number of locations throughout the universe—stars are powered by fusion. Humans have already figured out how to create temperatures high enough to achieve fusion on a large scale in thermonuclear weapons. A thermonuclear weapon such as a hydrogen bomb contains a nuclear fission bomb that, when exploded, gives off enough energy to produce the extremely high temperatures necessary for fusion to occur.

Figure \(\PageIndex{3}\): (a) This model is of the International Thermonuclear Experimental Reactor (ITER) reactor. Currently under construction in the south of France with an expected completion date of 2027, the ITER will be the world’s largest experimental Tokamak nuclear fusion reactor with a goal of achieving larg\times 10^{scale sustained energy production. (b) In 2012, the National Ignition Facility at Lawrence Livermore National Laboratory briefly produced over 500,000,000,000 watts (500 terawatts, or 500 TW) of peak power and delivered 1,850,000 joules (1.85 MJ) of energy, the largest laser energy ever produced and 1000 times the power usage of the entire United States in any given moment. Although lasting only a few billionths of a second, the 192 lasers attained the conditions needed for nuclear fusion ignition. This image shows the target prior to the laser shot. (credit a: modification of work by Stephan Mosel)

Another much more beneficial way to create fusion reactions is in a fusion reactor, a nuclear reactor in which fusion reactions of light nuclei are controlled. Because no solid materials are stable at such high temperatures, mechanical devices cannot contain the plasma in which fusion reactions occur. Two techniques to contain plasma at the density and temperature necessary for a fusion reaction are currently the focus of intensive research efforts: containment by a magnetic field and by the use of focused laser beams (Figure \(\PageIndex{3}\)). A number of large projects are working to attain one of the biggest goals in science: getting hydrogen fuel to ignite and produce more energy than the amount supplied to achieve the extremely high temperatures and pressures that are required for fusion. At the time of this writing, there are no self-sustaining fusion reactors operating in the world, although small-scale controlled fusion reactions have been run for very brief periods.Contributors

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).