8.2: Hybrid Atomic Orbitals
- Page ID
- 105591
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- Explain the concept of atomic orbital hybridization
- Determine the hybrid orbitals associated with various molecular geometries
Thinking in terms of overlapping atomic orbitals is one way for us to explain how chemical bonds form in diatomic molecules. However, to understand how molecules with more than two atoms form stable bonds, we require a more detailed model. As an example, let us consider the water molecule, in which we have one oxygen atom bonding to two hydrogen atoms. Oxygen has the electron configuration 1s22s22p4, with two unpaired electrons (one in each of the two 2p orbitals). Valence bond theory would predict that the two O–H bonds form from the overlap of these two 2p orbitals with the 1s orbitals of the hydrogen atoms. If this were the case, the bond angle would be 90°, as shown in Figure \(\PageIndex{1}\), because p orbitals are perpendicular to each other. Experimental evidence shows that the bond angle is 104.5°, not 90°. The prediction of the valence bond theory model does not match the real-world observations of a water molecule; a different model is needed.
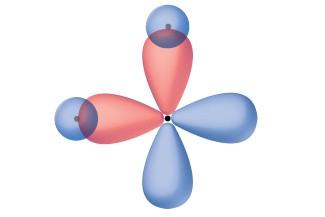
Figure \(\PageIndex{1}\): The hypothetical overlap of two of the 2p orbitals on an oxygen atom (red) with the 1s orbitals of two hydrogen atoms (blue) would produce a bond angle of 90°. This is not consistent with experimental evidence.1
Quantum-mechanical calculations suggest why the observed bond angles in H2O differ from those predicted by the overlap of the 1s orbital of the hydrogen atoms with the 2p orbitals of the oxygen atom. The mathematical expression known as the wave function, ψ, contains information about each orbital and the wavelike properties of electrons in an isolated atom. When atoms are bound together in a molecule, the wave functions combine to produce new mathematical descriptions that have different shapes. This process of combining the wave functions for atomic orbitals is called hybridization and is mathematically accomplished by the linear combination of atomic orbitals, LCAO, (a technique that we will encounter again later). The new orbitals that result are called hybrid orbitals. The valence orbitals in an isolated oxygen atom are a 2s orbital and three 2p orbitals. The valence orbitals in an oxygen atom in a water molecule differ; they consist of four equivalent hybrid orbitals that point approximately toward the corners of a tetrahedron (Figure \(\PageIndex{2}\)). Consequently, the overlap of the O and H orbitals should result in a tetrahedral bond angle (109.5°). The observed angle of 104.5° is experimental evidence for which quantum-mechanical calculations give a useful explanation: Valence bond theory must include a hybridization component to give accurate predictions.
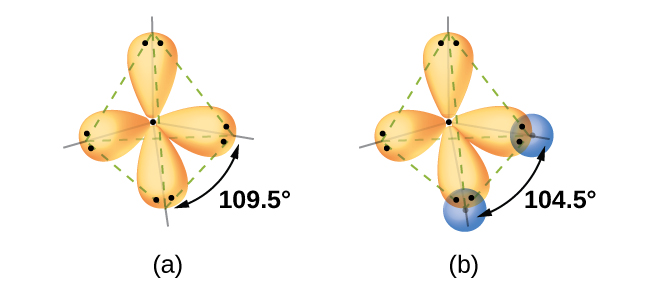
Figure \(\PageIndex{2}\): (a) A water molecule has four regions of electron density, so VSEPR theory predicts a tetrahedral arrangement of hybrid orbitals. (b) Two of the hybrid orbitals on oxygen contain lone pairs, and the other two overlap with the 1s orbitals of hydrogen atoms to form the O–H bonds in H2O. This description is more consistent with the experimental structure.
The following ideas are important in understanding hybridization:
- Hybrid orbitals do not exist in isolated atoms. They are formed only in covalently bonded atoms.
- Hybrid orbitals have shapes and orientations that are very different from those of the atomic orbitals in isolated atoms.
- A set of hybrid orbitals is generated by combining atomic orbitals. The number of hybrid orbitals in a set is equal to the number of atomic orbitals that were combined to produce the set.
- All orbitals in a set of hybrid orbitals are equivalent in shape and energy.
- The type of hybrid orbitals formed in a bonded atom depends on its electron-pair geometry as predicted by the VSEPR theory.
- Hybrid orbitals overlap to form σ bonds. Unhybridized orbitals overlap to form π bonds.
In the following sections, we shall discuss the common types of hybrid orbitals.
sp Hybridization
The beryllium atom in a gaseous BeCl2 molecule is an example of a central atom with no lone pairs of electrons in a linear arrangement of three atoms. There are two regions of valence electron density in the BeCl2 molecule that correspond to the two covalent Be–Cl bonds. To accommodate these two electron domains, two of the Be atom’s four valence orbitals will mix to yield two hybrid orbitals. This hybridization process involves mixing of the valence s orbital with one of the valence p orbitals to yield two equivalent sp hybrid orbitals that are oriented in a linear geometry (Figure \(\PageIndex{3}\)). In this figure, the set of sp orbitals appears similar in shape to the original p orbital, but there is an important difference. The number of atomic orbitals combined always equals the number of hybrid orbitals formed. The p orbital is one orbital that can hold up to two electrons. The sp set is two equivalent orbitals that point 180° from each other. The two electrons that were originally in the s orbital are now distributed to the two sp orbitals, which are half filled. In gaseous BeCl2, these half-filled hybrid orbitals will overlap with orbitals from the chlorine atoms to form two identical σ bonds.
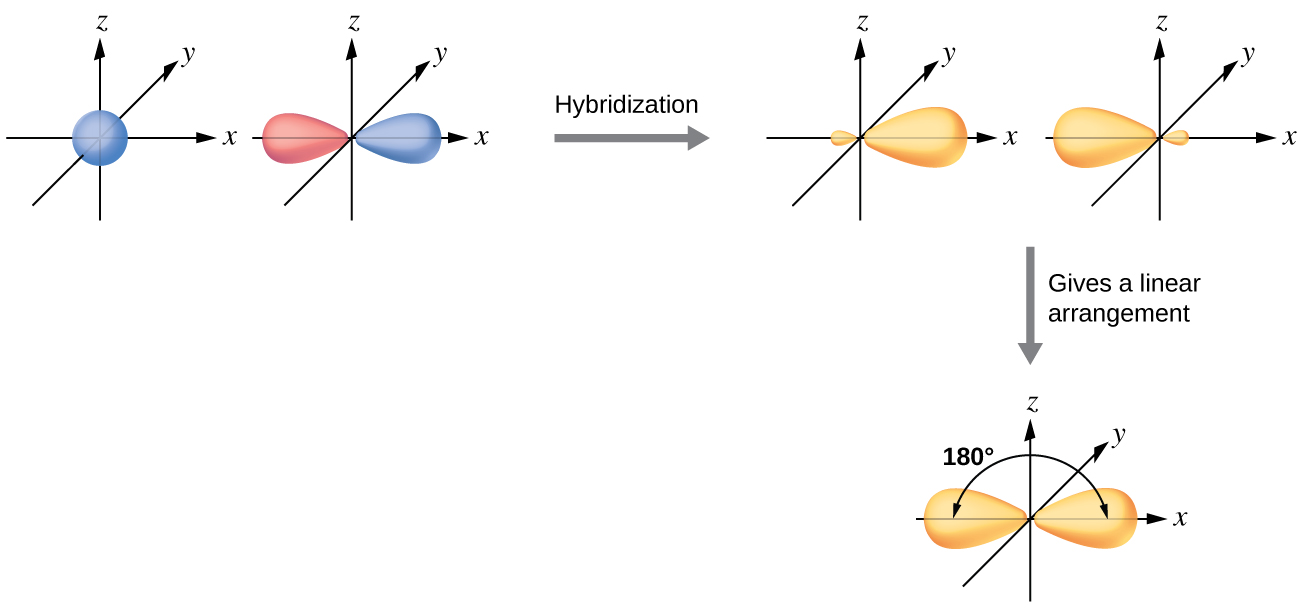
Figure \(\PageIndex{3}\): Hybridization of an s orbital (blue) and a p orbital (red) of the same atom produces two sp hybrid orbitals (yellow). Each hybrid orbital is oriented primarily in just one direction. Note that each sp orbital contains one lobe that is significantly larger than the other. The set of two sp orbitals are oriented at 180°, which is consistent with the geometry for two domains.
We illustrate the electronic differences in an isolated Be atom and in the bonded Be atom in the orbital energy-level diagram in Figure \(\PageIndex{4}\). These diagrams represent each orbital by a horizontal line (indicating its energy) and each electron by an arrow. Energy increases toward the top of the diagram. We use one upward arrow to indicate one electron in an orbital and two arrows (up and down) to indicate two electrons of opposite spin.

Figure \(\PageIndex{4}\): This orbital energy-level diagram shows the sp hybridized orbitals on Be in the linear BeCl2 molecule. Each of the two sp hybrid orbitals holds one electron and is thus half filled and available for bonding via overlap with a Cl 3p orbital.
When atomic orbitals hybridize, the valence electrons occupy the newly created orbitals. The Be atom had two valence electrons, so each of the sp orbitals gets one of these electrons. Each of these electrons pairs up with the unpaired electron on a chlorine atom when a hybrid orbital and a chlorine orbital overlap during the formation of the Be–Cl bonds. Any central atom surrounded by just two regions of valence electron density in a molecule will exhibit sp hybridization. Other examples include the mercury atom in the linear HgCl2 molecule, the zinc atom in Zn(CH3)2, which contains a linear C–Zn–C arrangement, and the carbon atoms in HCCH and CO2.
sp2 Hybridization
The valence orbitals of a central atom surrounded by three regions of electron density consist of a set of three sp2 hybrid orbitals and one unhybridized p orbital. This arrangement results from sp2 hybridization, the mixing of one s orbital and two p orbitals to produce three identical hybrid orbitals oriented in a trigonal planar geometry (Figure \(\PageIndex{5}\)).
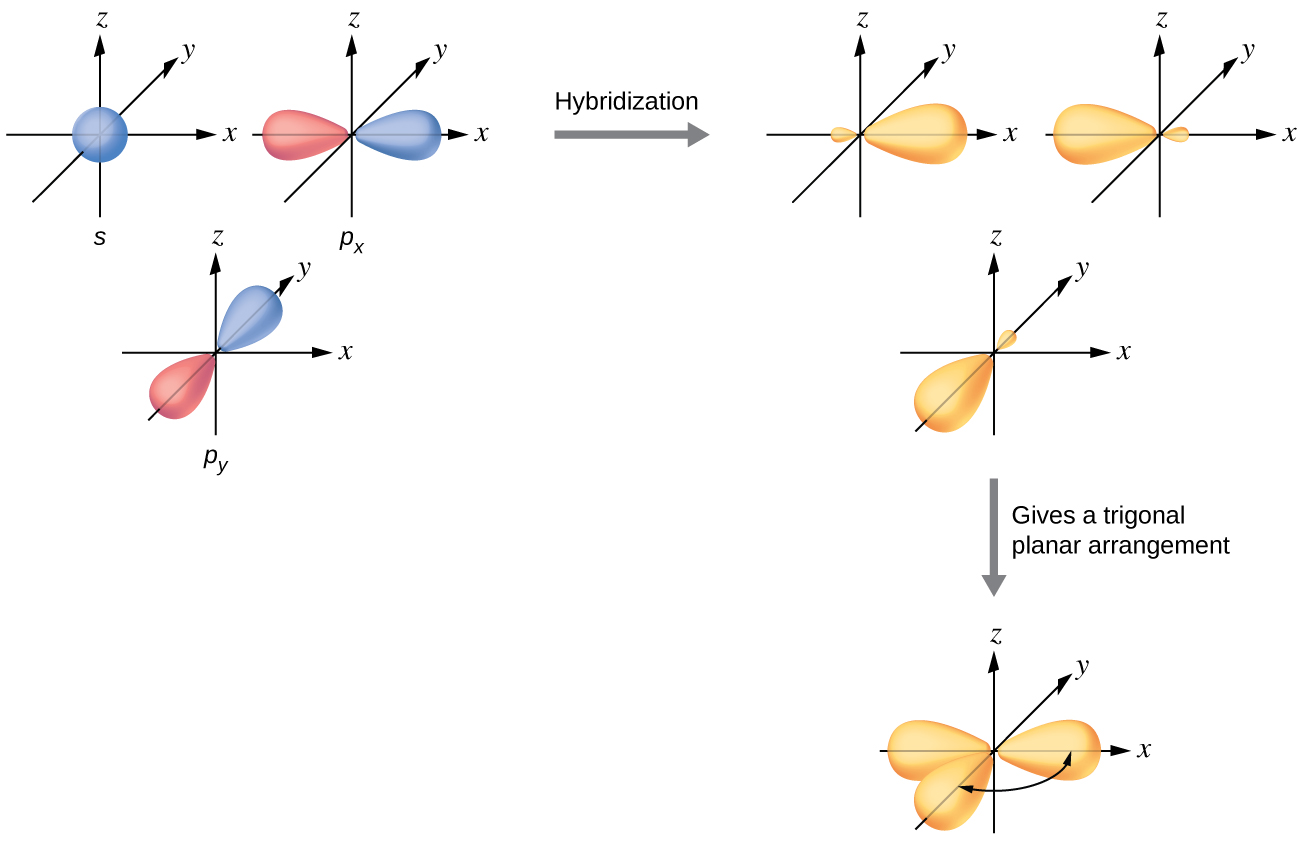
Figure \(\PageIndex{5}\): The hybridization of an s orbital (blue) and two p orbitals (red) produces three equivalent sp2 hybridized orbitals (yellow) oriented at 120° with respect to each other. The remaining unhybridized p orbital is not shown here, but is located along the z axis.
Although quantum mechanics yields the “plump” orbital lobes as depicted in Figure \(\PageIndex{5}\), sometimes for clarity these orbitals are drawn thinner and without the minor lobes, as in Figure \(\PageIndex{6}\), to avoid obscuring other features of a given illustration. We will use these “thinner” representations whenever the true view is too crowded to easily visualize.
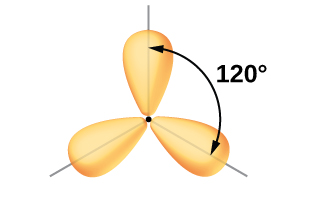
Figure \(\PageIndex{6}\): This alternate way of drawing the trigonal planar sp2 hybrid orbitals is sometimes used in more crowded figures.
The observed structure of the borane molecule, BH3, suggests sp2 hybridization for boron in this compound. The molecule is trigonal planar, and the boron atom is involved in three bonds to hydrogen atoms ( Figure \(\PageIndex{7}\)).
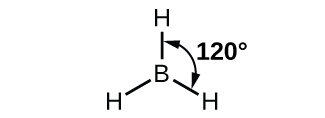
Figure \(\PageIndex{7}\): BH3 is an electron-deficient molecule with a trigonal planar structure.
We can illustrate the comparison of orbitals and electron distribution in an isolated boron atom and in the bonded atom in BH3 as shown in the orbital energy level diagram in Figure \(\PageIndex{8}\). We redistribute the three valence electrons of the boron atom in the three sp2 hybrid orbitals, and each boron electron pairs with a hydrogen electron when B–H bonds form.
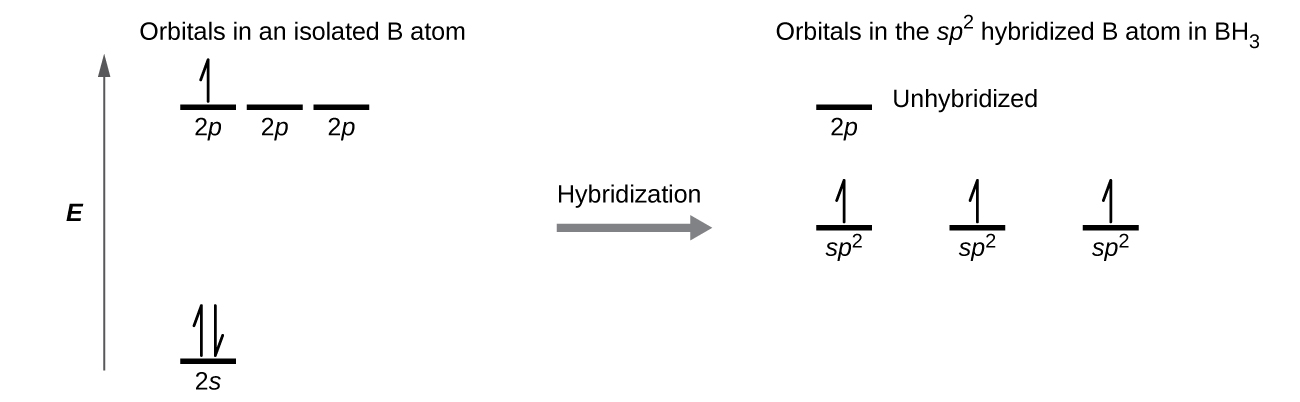
Figure \(\PageIndex{8}\): In an isolated B atom, there are one 2s and three 2p valence orbitals. When boron is in a molecule with three regions of electron density, three of the orbitals hybridize and create a set of three sp2 orbitals and one unhybridized 2p orbital. The three half-filled hybrid orbitals each overlap with an orbital from a hydrogen atom to form three σ bonds in BH3.
Any central atom surrounded by three regions of electron density will exhibit sp2 hybridization. This includes molecules with a lone pair on the central atom, such as ClNO (Figure \(\PageIndex{9}\)), or molecules with two single bonds and a double bond connected to the central atom, as in formaldehyde, CH2O, and ethene, H2CCH2.
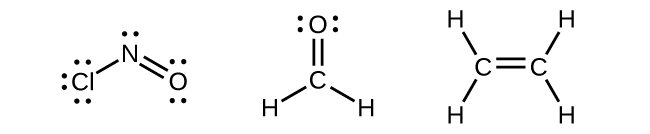
Figure \(\PageIndex{9}\): The central atom(s) in each of the structures shown contain three regions of electron density and are sp2 hybridized. As we know from the discussion of VSEPR theory, a region of electron density contains all of the electrons that point in one direction. A lone pair, an unpaired electron, a single bond, or a multiple bond would each count as one region of electron density.
sp3 Hybridization
The valence orbitals of an atom surrounded by a tetrahedral arrangement of bonding pairs and lone pairs consist of a set of four sp3 hybrid orbitals. The hybrids result from the mixing of one s orbital and all three p orbitals that produces four identical sp3 hybrid orbitals (Figure \(\PageIndex{10}\)). Each of these hybrid orbitals points toward a different corner of a tetrahedron.
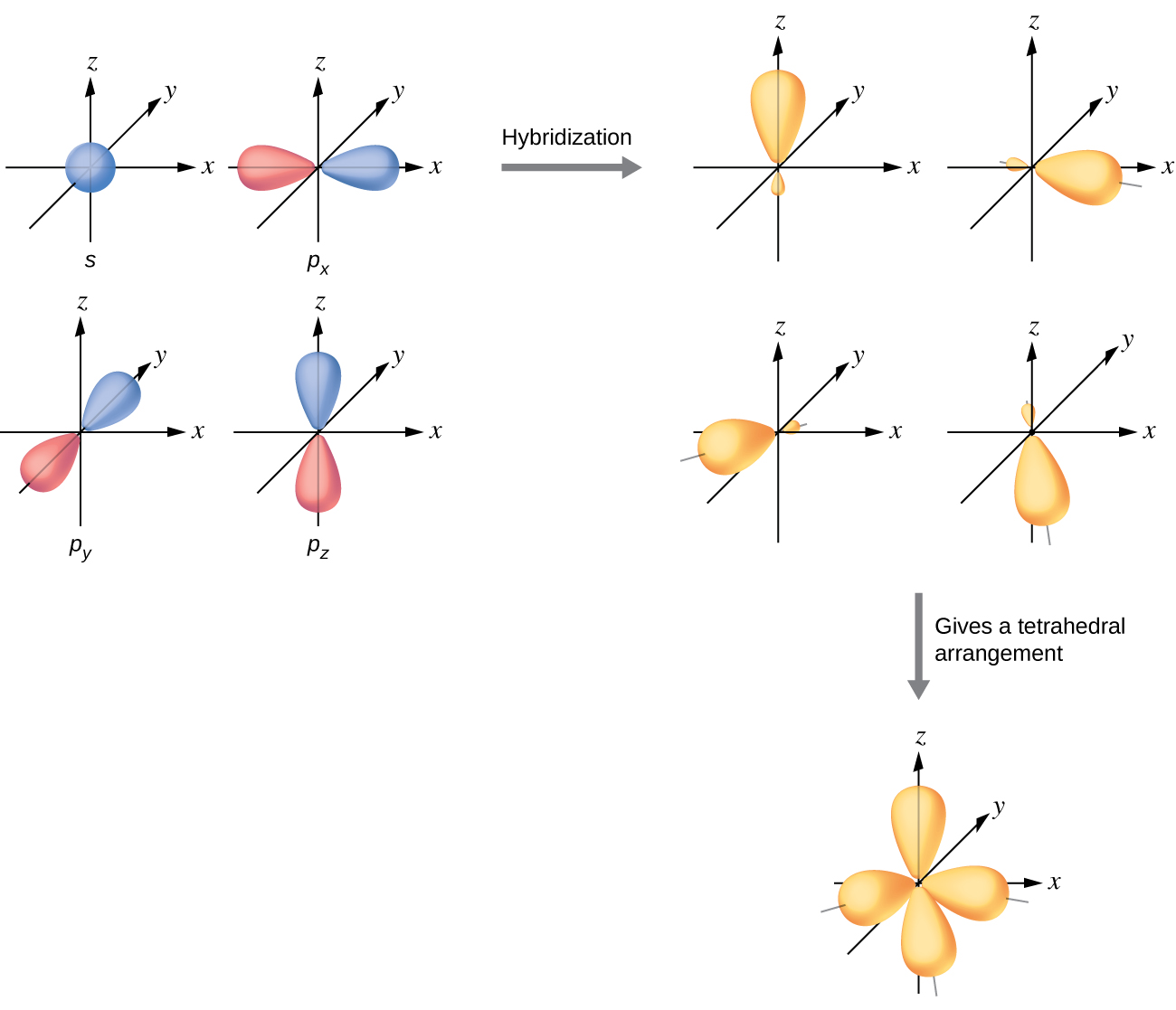
Figure \(\PageIndex{10}\): The hybridization of an s orbital (blue) and three p orbitals (red) produces four equivalent sp3 hybridized orbitals (yellow) oriented at 109.5° with respect to each other.
A molecule of methane, CH4, consists of a carbon atom surrounded by four hydrogen atoms at the corners of a tetrahedron. The carbon atom in methane exhibits sp3 hybridization. We illustrate the orbitals and electron distribution in an isolated carbon atom and in the bonded atom in CH4 in Figure \(\PageIndex{11}\). The four valence electrons of the carbon atom are distributed equally in the hybrid orbitals, and each carbon electron pairs with a hydrogen electron when the C–H bonds form.
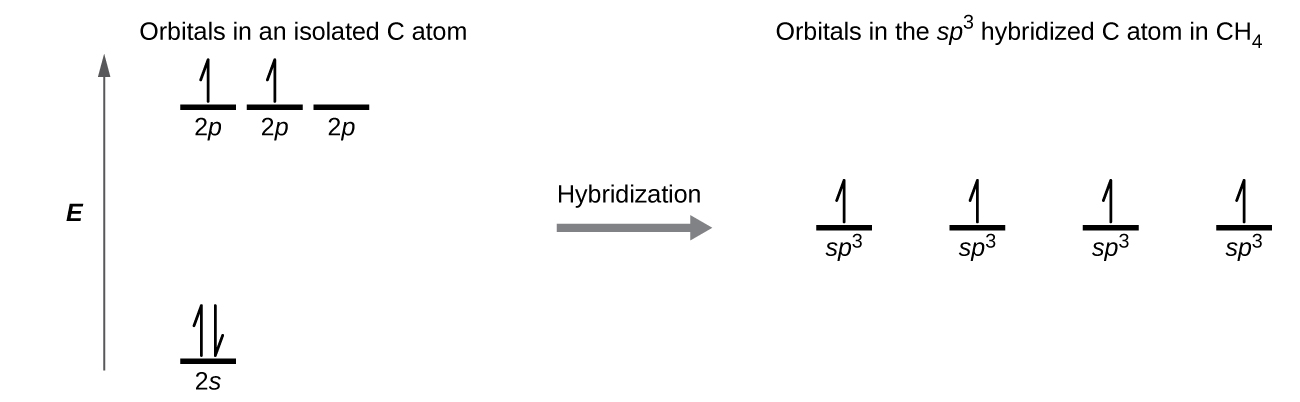
Figure \(\PageIndex{11}\): The four valence atomic orbitals from an isolated carbon atom all hybridize when the carbon bonds in a molecule like CH4 with four regions of electron density. This creates four equivalent sp3 hybridized orbitals. Overlap of each of the hybrid orbitals with a hydrogen orbital creates a C–H σ bond.
In a methane molecule, the 1s orbital of each of the four hydrogen atoms overlaps with one of the four sp3 orbitals of the carbon atom to form a sigma (σ) bond. This results in the formation of four strong, equivalent covalent bonds between the carbon atom and each of the hydrogen atoms to produce the methane molecule, CH4.
The structure of ethane, C2H6, is similar to that of methane in that each carbon in ethane has four neighboring atoms arranged at the corners of a tetrahedron—three hydrogen atoms and one carbon atom (Figure \(\PageIndex{10}\)). However, in ethane an sp3 orbital of one carbon atom overlaps end to end with an sp3 orbital of a second carbon atom to form a σ bond between the two carbon atoms. Each of the remaining sp3 hybrid orbitals overlaps with an s orbital of a hydrogen atom to form carbon–hydrogen σ bonds. The structure and overall outline of the bonding orbitals of ethane are shown in Figure \(\PageIndex{12}\). The orientation of the two CH3 groups is not fixed relative to each other. Experimental evidence shows that rotation around σ bonds occurs easily.
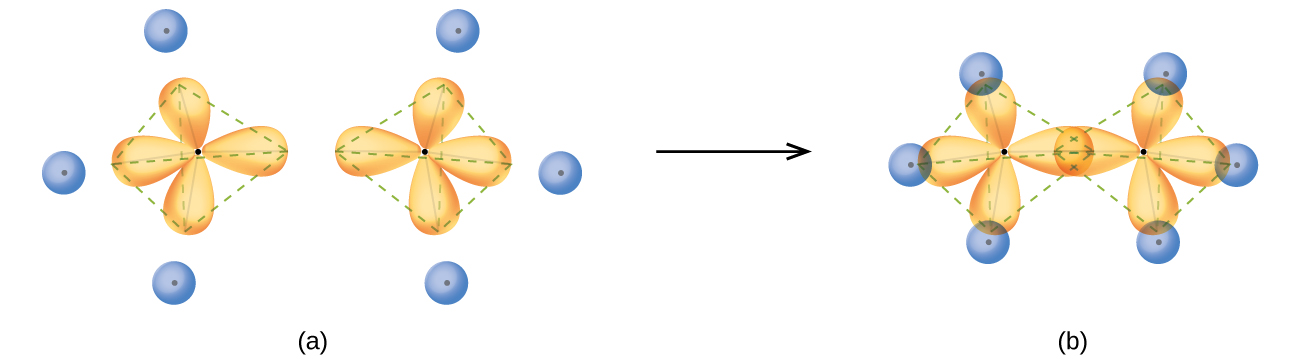
Figure \(\PageIndex{12}\): (a) In the ethane molecule, C2H6, each carbon has four sp3 orbitals. (b) These four orbitals overlap to form seven σ bonds.
An sp3 hybrid orbital can also hold a lone pair of electrons. For example, the nitrogen atom in ammonia is surrounded by three bonding pairs and a lone pair of electrons directed to the four corners of a tetrahedron. The nitrogen atom is sp3 hybridized with one hybrid orbital occupied by the lone pair.
The molecular structure of water is consistent with a tetrahedral arrangement of two lone pairs and two bonding pairs of electrons. Thus we say that the oxygen atom is sp3 hybridized, with two of the hybrid orbitals occupied by lone pairs and two by bonding pairs. Since lone pairs occupy more space than bonding pairs, structures that contain lone pairs have bond angles slightly distorted from the ideal. Perfect tetrahedra have angles of 109.5°, but the observed angles in ammonia (107.3°) and water (104.5°) are slightly smaller. Other examples of sp3 hybridization include CCl4, PCl3, and NCl3.
sp3d and sp3d2 Hybridization
To describe the five bonding orbitals in a trigonal bipyramidal arrangement, we must use five of the valence shell atomic orbitals (the s orbital, the three p orbitals, and one of the d orbitals), which gives five sp3d hybrid orbitals. With an octahedral arrangement of six hybrid orbitals, we must use six valence shell atomic orbitals (the s orbital, the three p orbitals, and two of the d orbitals in its valence shell), which gives six sp3d2 hybrid orbitals. These hybridizations are only possible for atoms that have d orbitals in their valence subshells (that is, not those in the first or second period).
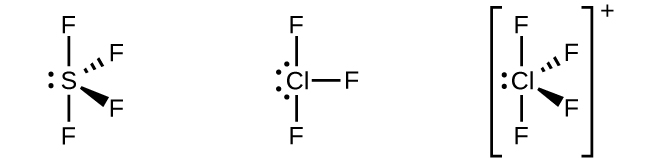
Figure \(\PageIndex{13}\): The three compounds pictured exhibit sp3d hybridization in the central atom and a trigonal bipyramid form. SF4 and
In a molecule of phosphorus pentachloride, PCl5, there are five P–Cl bonds (thus five pairs of valence electrons around the phosphorus atom) directed toward the corners of a trigonal bipyramid. We use the 3s orbital, the three 3p orbitals, and one of the 3d orbitals to form the set of five sp3d hybrid orbitals (Figure \(\PageIndex{13}\)) that are involved in the P–Cl bonds. Other atoms that exhibit sp3d hybridization include the sulfur atom in SF4 and the chlorine atoms in ClF3 and in \(\ce{ClF4+}\)
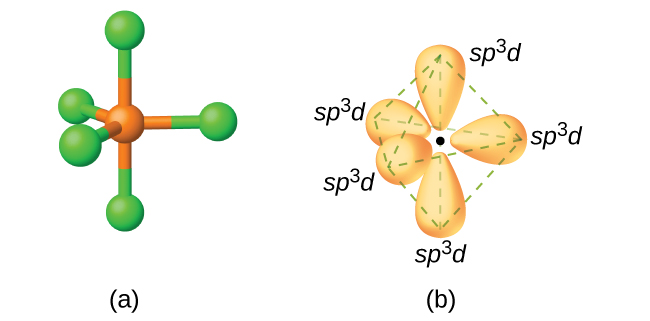
Figure \(\PageIndex{14}\): (a) The five regions of electron density around phosphorus in PCl5 require five hybrid sp3d orbitals. (b) These orbitals combine to form a trigonal bipyramidal structure with each large lobe of the hybrid orbital pointing at a vertex. As before, there are also small lobes pointing in the opposite direction for each orbital (not shown for clarity).
The sulfur atom in sulfur hexafluoride, SF6, exhibits sp3d2 hybridization. A molecule of sulfur hexafluoride has six bonding pairs of electrons connecting six fluorine atoms to a single sulfur atom. There are no lone pairs of electrons on the central atom. To bond six fluorine atoms, the 3s orbital, the three 3p orbitals, and two of the 3d orbitals form six equivalent sp3d2 hybrid orbitals, each directed toward a different corner of an octahedron. Other atoms that exhibit sp3d2 hybridization include the phosphorus atom in
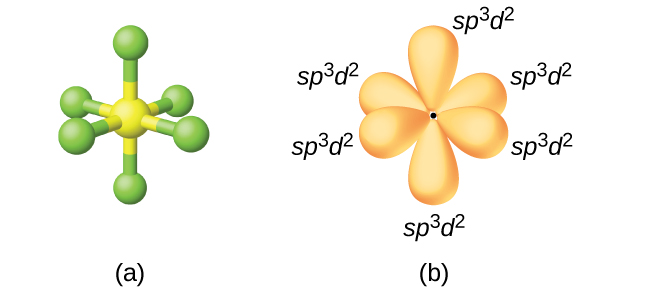
Figure \(\PageIndex{15}\): (a) Sulfur hexafluoride, SF6, has an octahedral structure that requires sp3d2 hybridization. (b) The six sp3d2 orbitals form an octahedral structure around sulfur. Again, the minor lobe of each orbital is not shown for clarity.
Assignment of Hybrid Orbitals to Central Atoms
The hybridization of an atom is determined based on the number of regions of electron density that surround it. The geometrical arrangements characteristic of the various sets of hybrid orbitals are shown in Figure \(\PageIndex{16}\). These arrangements are identical to those of the electron-pair geometries predicted by VSEPR theory. VSEPR theory predicts the shapes of molecules, and hybrid orbital theory provides an explanation for how those shapes are formed. To find the hybridization of a central atom, we can use the following guidelines:
- Determine the Lewis structure of the molecule.
- Determine the number of regions of electron density around an atom using VSEPR theory, in which single bonds, multiple bonds, radicals, and lone pairs each count as one region.
- Assign the set of hybridized orbitals from Figure \(\PageIndex{16}\) that corresponds to this geometry.
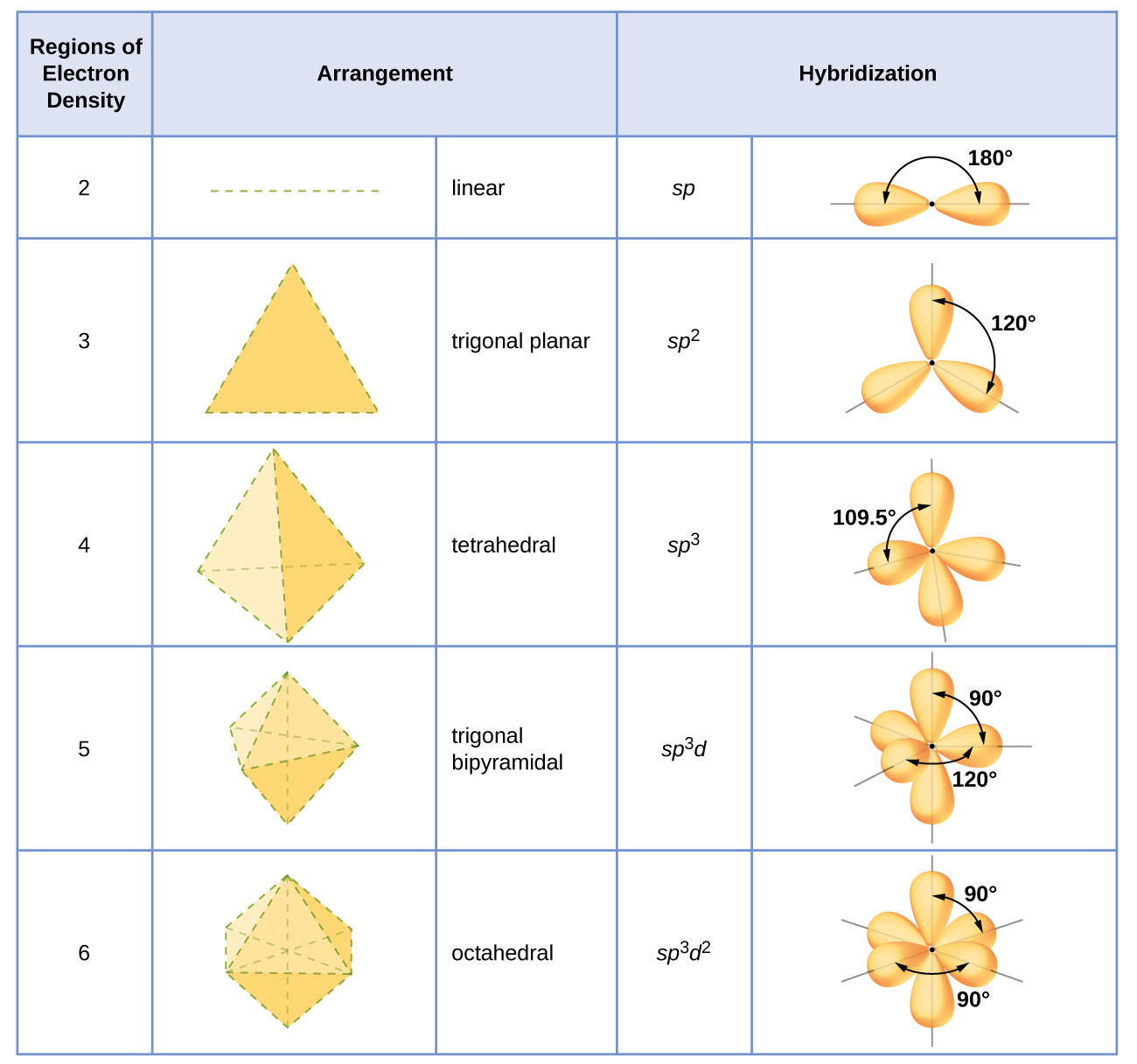
Figure \(\PageIndex{16}\): The shapes of hybridized orbital sets are consistent with the electron-pair geometries. For example, an atom surrounded by three regions of electron density is sp2 hybridized, and the three sp2 orbitals are arranged in a trigonal planar fashion.
It is important to remember that hybridization was devised to rationalize experimentally observed molecular geometries, not the other way around.
The model works well for molecules containing small central atoms, in which the valence electron pairs are close together in space. However, for larger central atoms, the valence-shell electron pairs are farther from the nucleus, and there are fewer repulsions. Their compounds exhibit structures that are often not consistent with VSEPR theory, and hybridized orbitals are not necessary to explain the observed data.

For example, we have discussed the H–O–H bond angle in H2O, 104.5°, which is more consistent with sp3 hybrid orbitals (109.5°) on the central atom than with 2p orbitals (90°). Sulfur is in the same group as oxygen, and H2S has a similar Lewis structure. However, it has a much smaller bond angle (92.1°), which indicates much less hybridization on sulfur than oxygen. Continuing down the group, tellurium is even larger than sulfur, and for H2Te, the observed bond angle (90°) is consistent with overlap of the 5p orbitals, without invoking hybridization. We invoke hybridization where it is necessary to explain the observed structures.
Example \(\PageIndex{1}\): Assigning Hybridization
Ammonium sulfate is important as a fertilizer. What is the hybridization of the sulfur atom in the sulfate ion,
Solution
The Lewis structure of sulfate shows there are four regions of electron density.
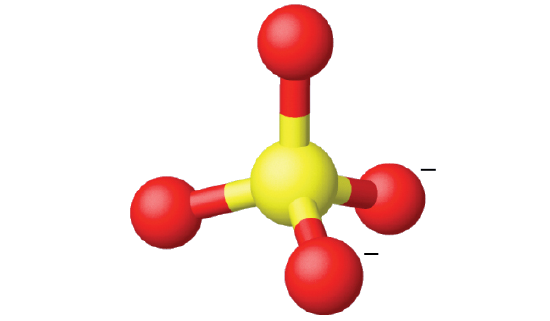
The hybridization is sp3. since the carbon has a tetrahedral geometry (Figure \(\PageIndex{16}\)).
Exercise \(\PageIndex{1}\)
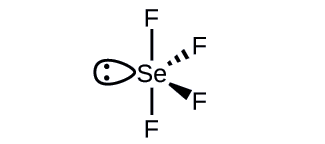
What is the hybridization of the selenium atom in SeF4?
- Answer
-
The selenium atom is sp3d hybridized.
Example \(\PageIndex{2}\): Assigning Hybridization
Urea, NH2C(O)NH2, is sometimes used as a source of nitrogen in fertilizers. What is the hybridization of each nitrogen and carbon atom in urea?
Solution
The Lewis structure of urea is
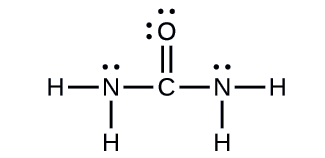
The nitrogen atoms are surrounded by four regions of electron density, which arrange themselves in a tetrahedral electron-pair geometry. The hybridization in a tetrahedral arrangement is sp3 (Figure \(\PageIndex{16}\)). This is the hybridization of the nitrogen atoms in urea.
The carbon atom is surrounded by three regions of electron density, positioned in a trigonal planar arrangement. The hybridization in a trigonal planar electron pair geometry is sp2 (Figure \(\PageIndex{16}\)), which is the hybridization of the carbon atom in urea.
Exercise \(\PageIndex{1}\)
Acetic acid, H3CC(O)OH, is the molecule that gives vinegar its odor and sour taste. What is the hybridization of the two carbon atoms in acetic acid?
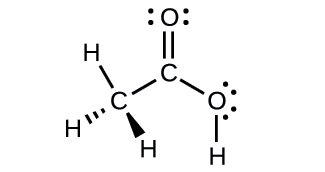
- Answer
-
H3C, sp3; C(O)OH, sp2
Summary
We can use hybrid orbitals, which are mathematical combinations of some or all of the valence atomic orbitals, to describe the electron density around covalently bonded atoms. These hybrid orbitals either form sigma (σ) bonds directed toward other atoms of the molecule or contain lone pairs of electrons. We can determine the type of hybridization around a central atom from the geometry of the regions of electron density about it. Two such regions imply sp hybridization; three, sp2 hybridization; four, sp3 hybridization; five, sp3d hybridization; and six, sp3d2 hybridization. Pi (π) bonds are formed from unhybridized atomic orbitals (p or d orbitals).
Footnotes
- Note that orbitals may sometimes be drawn in an elongated “balloon” shape rather than in a more realistic “plump” shape in order to make the geometry easier to visualize.
Glossary
- hybrid orbital
- orbital created by combining atomic orbitals on a central atom
- hybridization
- model that describes the changes in the atomic orbitals of an atom when it forms a covalent compound
- sp hybrid orbital
- one of a set of two orbitals with a linear arrangement that results from combining one s and one p orbital
- sp2 hybrid orbital
- one of a set of three orbitals with a trigonal planar arrangement that results from combining one s and two p orbitals
- sp3 hybrid orbital
- one of a set of four orbitals with a tetrahedral arrangement that results from combining one s and three p orbitals
- sp3d hybrid orbital
- one of a set of five orbitals with a trigonal bipyramidal arrangement that results from combining one s, three p, and one d orbital
- sp3d2 hybrid orbital
- one of a set of six orbitals with an octahedral arrangement that results from combining one s, three p, and two d orbitals
Contributors
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).


