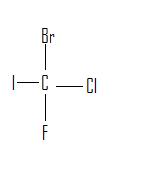
Stereoisomers are isomers that differ in spatial arrangement of atoms, rather than order of atomic connectivity. One of their most interesting type of isomer is the mirror-image stereoisomers, a non-superimposable set of two molecules that are mirror image of one another. The existence of these molecules are determined by concept known as chirality.
Introduction
Organic compounds, molecules created around a chain of carbon atom (more commonly known as carbon backbone), play an essential role in the chemistry of life. These molecules derive their importance from the energy they carry, mainly in a form of potential energy between atomic molecules. Since such potential force can be widely affected due to changes in atomic placement, it is important to understand the concept of an isomer, a molecule sharing same atomic make up as another but differing in structural arrangements. This article will be devoted to a specific isomers called stereoisomers and its property of chirality (Figure 1).
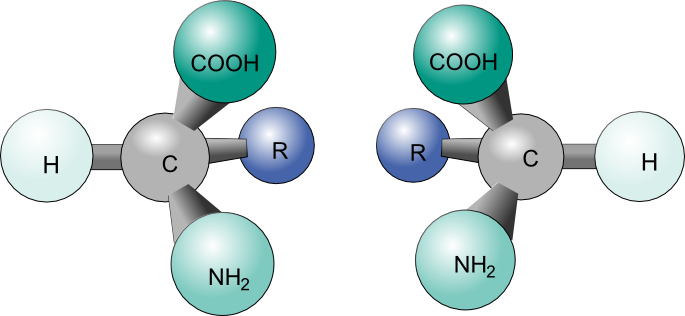
Figure 1: Two enantiomers of a tetrahedral complex.
The concepts of steroisomerism and chirality command great deal of importance in modern organic chemistry, as these ideas helps to understand the physical and theoretical reasons behind the formation and structures of numerous organic molecules, the main reason behind the energy embedded in these essential chemicals. In contrast to more well-known constitutional isomerism, which develops isotopic compounds simply by different atomic connectivity, stereoisomerism generally maintains equal atomic connections and orders of building blocks as well as having same numbers of atoms and types of elements.
What, then, makes stereoisomers so unique? To answer this question, the learner must be able to think and imagine in not just two-dimensional images, but also three-dimensional space. This is due to the fact that stereoisomers are isomers because their atoms are different from others in terms of spatial arrangement.
Spatial Arrangement
First and foremost, one must understand the concept of spatial arrangement in order to understand stereoisomerism and chirality. Spatial arrangement of atoms concern how different atomic particles and molecules are situated about in the space around the organic compound, namely its carbon chain. In this sense, spatial arrangement of an organic molecule are different another if an atom is shifted in any three-dimensional direction by even one degree. This opens up a very broad possibility of different molecules, each with their unique placement of atoms in three-dimensional space .
Stereoisomers
Stereoisomers are, as mentioned above, contain different types of isomers within itself, each with distinct characteristics that further separate each other as different chemical entities having different properties. Type called entaniomer are the previously-mentioned mirror-image stereoisomers, and will be explained in detail in this article. Another type, diastereomer, has different properties and will be introduced afterwards.
Enantiomers
This type of stereoisomer is the essential mirror-image, non-superimposable type of stereoisomer introduced in the beginning of the article. Figure 3 provides a perfect example; note that the gray plane in the middle demotes the mirror plane.
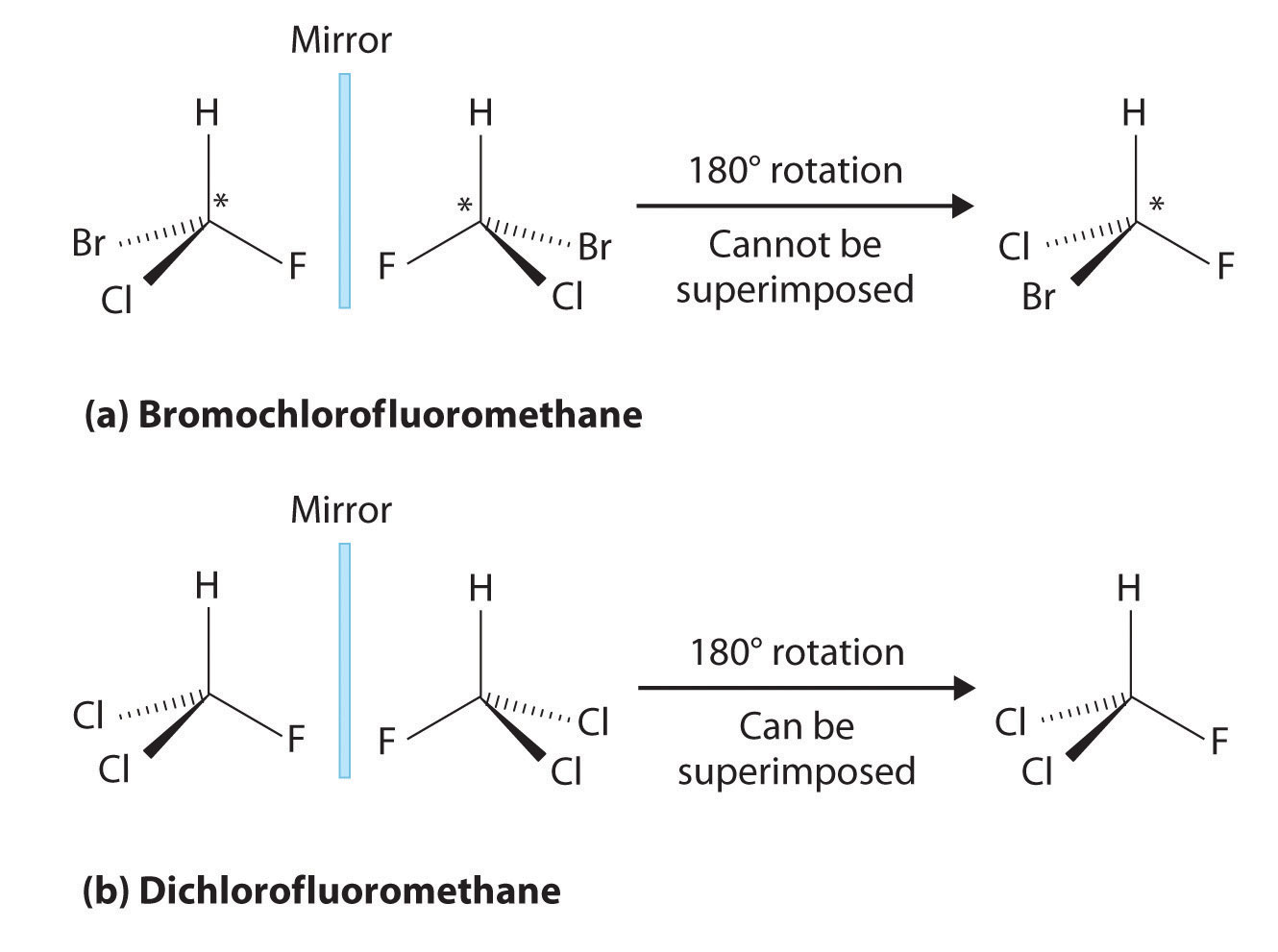
Figure 2: Comparison of Chiral and Achiral Molecules. (a) Bromochlorofluoromethane is a chiral molecule whose stereocenter is designated with an asterisk. Rotation of its mirror image does not generate the original structure. To superimpose the mirror images, bonds must be broken and reformed. (b) In contrast, dichlorofluoromethane and its mirror image can be rotated so they are superimposable.
Note that even if one were to flip over the left molecule over to the right, the atomic spatial arrangement will not be equal. This is equivalent to the left hand - right hand relationship, and is aptly referred to as 'handedness' in molecules. This can be somewhat counter-intuitive, so this article recommends the reader try the 'hand' example. Place both palm facing up, and hands next to each other. Now flip either side over to the other. One hand should be showing the back of the hand, while the other one is showing the palm. They are not same and non-superimposable.
This is where the concept of chirality comes in as one of the most essential and defining idea of stereoisomerism.
Chirality
Chirality essentially means 'mirror-image, non-superimposable molecules', and to say that a molecule is chiral is to say that its mirror image (it must have one) is not the same as it self. Whether a molecule is chiral or achiral depends upon a certain set of overlapping conditions. Figure 4 shows an example of two molecules, chiral and achiral, respectively. Notice the distinct characteristic of the achiral molecule: it possesses two atoms of same element. In theory and reality, if one were to create a plane that runs through the other two atoms, they will be able to create what is known as bisecting plane: The images on either side of the plan is the same as the other (Figure 4).
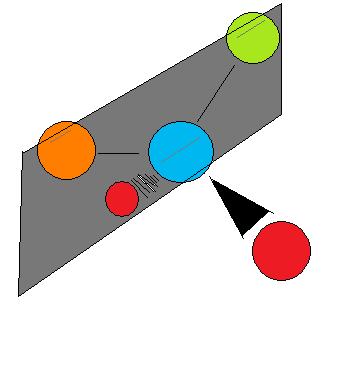
Figure 4.
In this case, the molecule is considered 'achiral'. In other words, to distinguish chiral molecule from an achiral molecule, one must search for the existence of the bisecting plane in a molecule. All chiral molecules are deprive of bisecting plane, whether simple or complex.
As a universal rule, no molecule with different surrounding atoms are achiral. Chirality is a simple but essential idea to support the concept of stereoisomerism, being used to explain one type of its kind. The chemical properties of the chiral molecule differs from its mirror image, and in this lies the significance of chilarity in relation to modern organic chemistry.
Compounds with Multiple Chiral Centers
We turn our attention next to molecules which have more than one stereocenter. We will start with a common four-carbon sugar called D-erythrose.
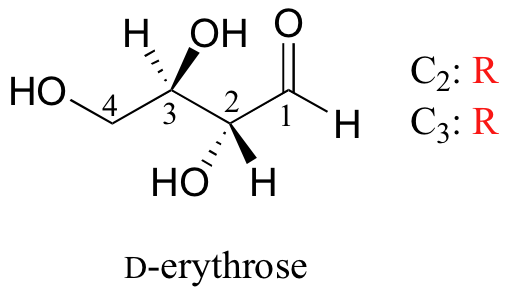
A note on sugar nomenclature: biochemists use a special system to refer to the stereochemistry of sugar molecules, employing names of historical origin in addition to the designators 'D' and 'L'. You will learn about this system if you take a biochemistry class. We will use the D/L designations here to refer to different sugars, but we won't worry about learning the system.
As you can see, D-erythrose is a chiral molecule: C2 and C3 are stereocenters, both of which have the R configuration. In addition, you should make a model to convince yourself that it is impossible to find a plane of symmetry through the molecule, regardless of the conformation. Does D-erythrose have an enantiomer? Of course it does – if it is a chiral molecule, it must. The enantiomer of erythrose is its mirror image, and is named L-erythrose (once again, you should use models to convince yourself that these mirror images of erythrose are not superimposable).
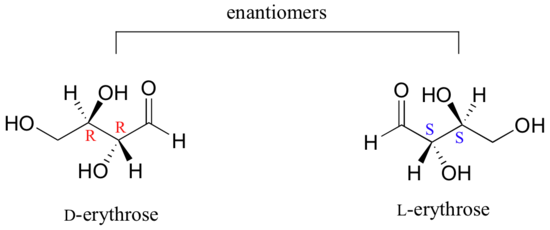
Notice that both chiral centers in L-erythrose both have the S configuration. In a pair of enantiomers, all of the chiral centers are of the opposite configuration.
What happens if we draw a stereoisomer of erythrose in which the configuration is S at C2 and R at C3? This stereoisomer, which is a sugar called D-threose, is not a mirror image of erythrose. D-threose is a diastereomer of both D-erythrose and L-erythrose.
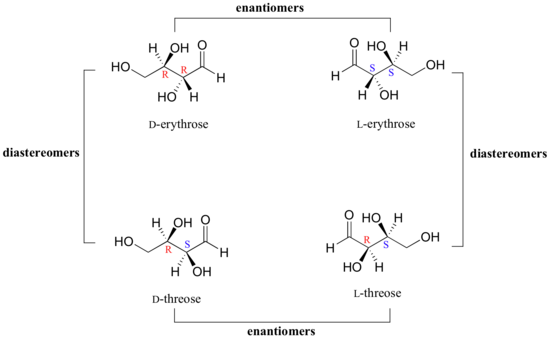
The definition of diastereomers is simple: if two molecules are stereoisomers (same molecular formula, same connectivity, different arrangement of atoms in space) but are not enantiomers, then they are diastereomers by default. In practical terms, this means that at least one - but not all - of the chiral centers are opposite in a pair of diastereomers. By definition, two molecules that are diastereomers are not mirror images of each other.
L-threose, the enantiomer of D-threose, has the R configuration at C2 and the S configuration at C3. L-threose is a diastereomer of both erythrose enantiomers.
In general, a structure with n stereocenters will have 2n different stereoisomers. (We are not considering, for the time being, the stereochemistry of double bonds – that will come later). For example, let's consider the glucose molecule in its open-chain form (recall that many sugar molecules can exist in either an open-chain or a cyclic form). There are two enantiomers of glucose, called D-glucose and L-glucose. The D-enantiomer is the common sugar that our bodies use for energy. It has n = 4 stereocenters, so therefore there are 2n = 24 = 16 possible stereoisomers (including D-glucose itself).
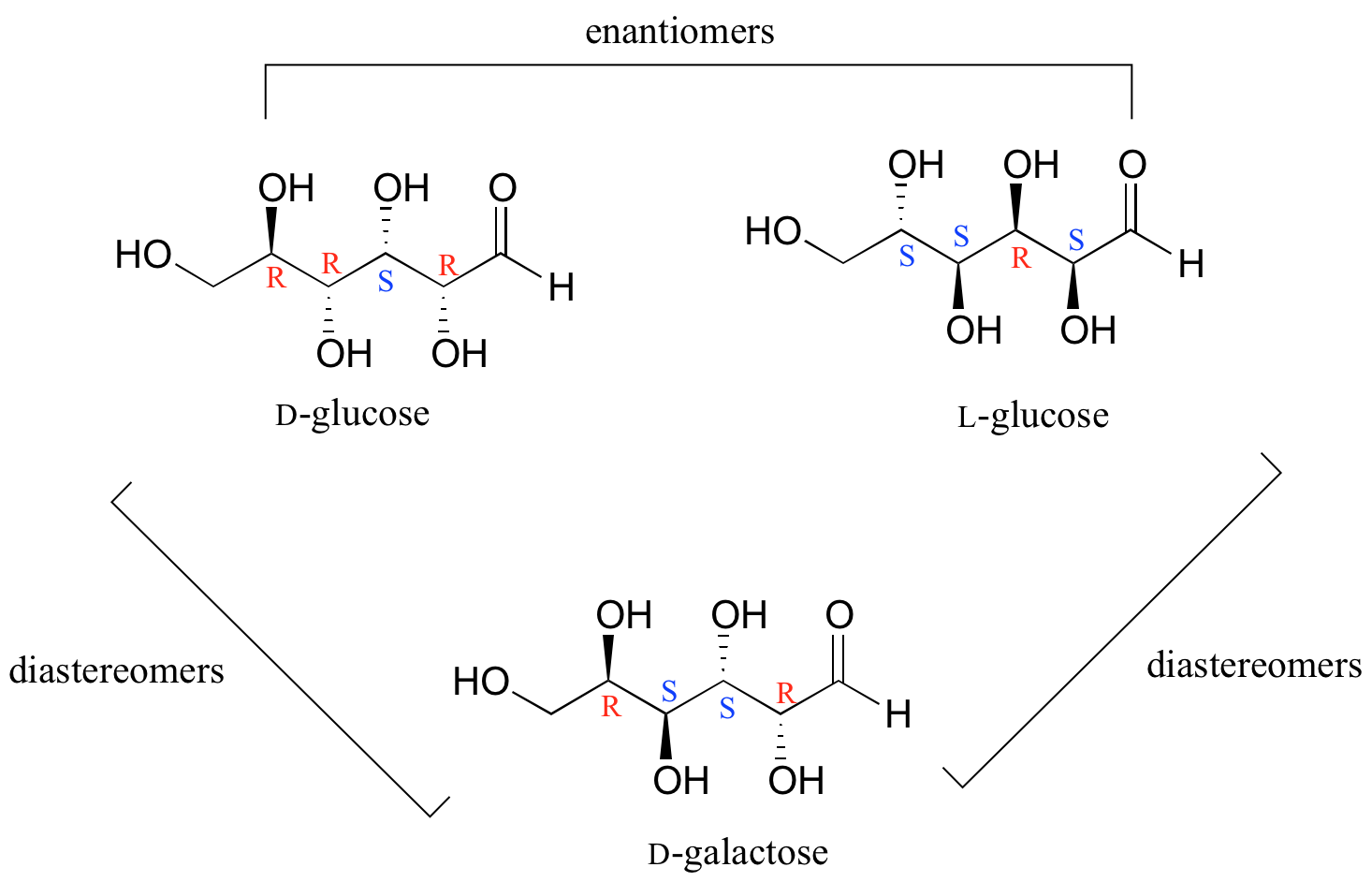
In L-glucose, all of the stereocenters are inverted relative to D-glucose. That leaves 14 diastereomers of D-glucose: these are molecules in which at least one, but not all, of the stereocenters are inverted relative to D-glucose. One of these 14 diastereomers, a sugar called D-galactose, is shown above: in D-galactose, one of four stereocenters is inverted relative to D-glucose. Diastereomers which differ in only one stereocenter (out of two or more) are called epimers. D-glucose and D-galactose can therefore be refered to as epimers as well as diastereomers.
Example 3.10
Draw the structure of L-galactose, the enantiomer of D-galactose.
Solution









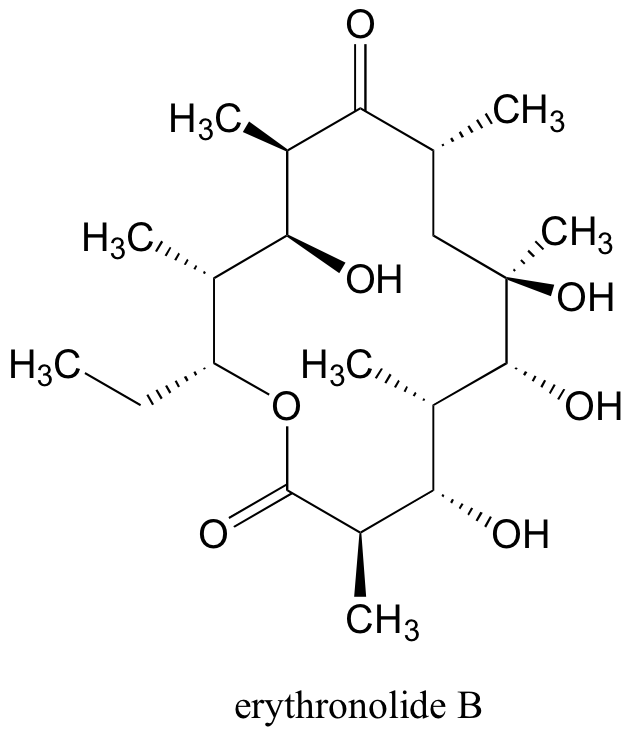
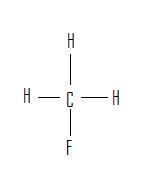 2.
2.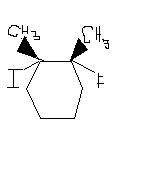 3.
3.