1.5: Heat Capacity and Calorimetry
- Last updated
- Save as PDF
- Page ID
- 42251
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Learning Objectives
- Explain the technique of calorimetry
- Calculate and interpret heat and related properties using typical calorimetry data
- To use calorimetric data to calculate enthalpy changes.
Heat Capacity
We now introduce two concepts useful in describing heat flow and temperature change. The heat capacity (\(C\)) of a body of matter is the quantity of heat (\(q\)) it absorbs or releases when it experiences a temperature change (\(ΔT\)) of 1 degree Celsius (or equivalently, 1 kelvin)
\[C=\dfrac{q}{ΔT} \label{12.3.1} \]
Heat capacity is determined by both the type and amount of substance that absorbs or releases heat. It is therefore an extensive property—its value is proportional to the amount of the substance.
For example, consider the heat capacities of two cast iron frying pans. The heat capacity of the large pan is five times greater than that of the small pan because, although both are made of the same material, the mass of the large pan is five times greater than the mass of the small pan. More mass means more atoms are present in the larger pan, so it takes more energy to make all of those atoms vibrate faster. The heat capacity of the small cast iron frying pan is found by observing that it takes 18,140 J of energy to raise the temperature of the pan by 50.0 °C
\[C_{\text{small pan}}=\dfrac{18,140\, J}{50.0\, °C} =363\; J/°C \label{12.3.2} \nonumber\]
The larger cast iron frying pan, while made of the same substance, requires 90,700 J of energy to raise its temperature by 50.0 °C. The larger pan has a (proportionally) larger heat capacity because the larger amount of material requires a (proportionally) larger amount of energy to yield the same temperature change:
\[C_{\text{large pan}}=\dfrac{90,700\, J}{50.0\,°C}=1814\, J/°C \label{12.3.3} \nonumber\]
The specific heat capacity (\(c\)) of a substance, commonly called its specific heat, is the quantity of heat required to raise the temperature of 1 gram of a substance by 1 degree Celsius (or 1 kelvin):
\[c = \dfrac{q}{m\Delta T} \label{12.3.4} \]
Specific heat capacity depends only on the kind of substance absorbing or releasing heat. It is an intensive property—the type, but not the amount, of the substance is all that matters. For example, the small cast iron frying pan has a mass of 808 g. The specific heat of iron (the material used to make the pan) is therefore:
\[c_{iron}=\dfrac{18,140\; J}{(808\; g)(50.0\;°C)} = 0.449\; J/g\; °C \label{12.3.5} \nonumber\]
The large frying pan has a mass of 4040 g. Using the data for this pan, we can also calculate the specific heat of iron:
\[c_{iron}=\dfrac{90,700 J}{(4,040\; g)(50.0\;°C)}=0.449\; J/g\; °C \label{12.3.6} \nonumber\]
Although the large pan is more massive than the small pan, since both are made of the same material, they both yield the same value for specific heat (for the material of construction, iron). Note that specific heat is measured in units of energy per temperature per mass and is an intensive property, being derived from a ratio of two extensive properties (heat and mass). The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and has units of J/mol °C (Figure \(\PageIndex{1}\)).

The heat capacity of an object depends on both its mass and its composition. For example, doubling the mass of an object doubles its heat capacity. Consequently, the amount of substance must be indicated when the heat capacity of the substance is reported. The molar heat capacity (Cp) is the amount of energy needed to increase the temperature of 1 mol of a substance by 1°C; the units of Cp are thus J/(mol•°C).The subscript p indicates that the value was measured at constant pressure. The specific heat (\(c_s\)) is the amount of energy needed to increase the temperature of 1 g of a substance by 1°C; its units are thus J/(g•°C).
We can relate the quantity of a substance, the amount of heat transferred, its heat capacity, and the temperature change either via moles (Equation \(\ref{12.3.7}\)) or mass (Equation \(\ref{12.3.8}\)):
\[q = nc_p ΔT \label{12.3.7}\]
where
- \(n\) is the number of moles of substance and
- \(c_p\) is the molar heat capacity (i.e., heat capacity per mole of substance), and
- \(ΔT= T_{final} − T_{initial}\) is the temperature change.
\[q = mc_s ΔT \label{12.3.8}\]
where
- \(m\) is the mass of substance in grams,
- \(c_s\) is the specific heat (i.e., heat capacity per gram of substance), and
- \(ΔT= T_{final} − T_{initial}\) is the temperature change.
Both Equations \ref{12.3.7} and \ref{12.3.8} are under constant pressure (which matters) and both show that we know the amount of a substance and its specific heat (for mass) or molar heat capcity (for moles), we can determine the amount of heat, \(q\), entering or leaving the substance by measuring the temperature change before and after the heat is gained or lost.
The specific heats of some common substances are given in Table \(\PageIndex{1}\). Note that the specific heat values of most solids are less than 1 J/(g•°C), whereas those of most liquids are about 2 J/(g•°C). Water in its solid and liquid states is an exception. The heat capacity of ice is twice as high as that of most solids; the heat capacity of liquid water, 4.184 J/(g•°C), is one of the highest known. The specific heat of a substance varies somewhat with temperature. However, this variation is usually small enough that we will treat specific heat as constant over the range of temperatures that will be considered in this chapter. Specific heats of some common substances are listed in Table \(\PageIndex{1}\).
| Substance | Symbol (state) | Specific Heat (J/g °C) |
|---|---|---|
| helium | He(g) | 5.193 |
| water | H2O(l) | 4.184 |
| ethanol | C2H6O(l) | 2.376 |
| ice | H2O(s) | 2.093 (at −10 °C) |
| water vapor | H2O(g) | 1.864 |
| nitrogen | N2(g) | 1.040 |
| air | mixture | 1.007 |
| oxygen | O2(g) | 0.918 |
| aluminum | Al(s) | 0.897 |
| carbon dioxide | CO2(g) | 0.853 |
| argon | Ar(g) | 0.522 |
| iron | Fe(s) | 0.449 |
| copper | Cu(s) | 0.385 |
| lead | Pb(s) | 0.130 |
| gold | Au(s) | 0.129 |
| silicon | Si(s) | 0.712 |
| quartz | \(\ce{SiO2 (s)}\) | 0.730 |
The value of \(C\) is intrinsically a positive number, but \(ΔT\) and \(q\) can be either positive or negative, and they both must have the same sign. If \(ΔT\) and \(q\) are positive, then heat flows from the surroundings into an object. If \(ΔT\) and \(q\) are negative, then heat flows from an object into its surroundings.
If a substance gains thermal energy, its temperature increases, its final temperature is higher than its initial temperature, then \(ΔT>0 \) and \(q\) is positive. If a substance loses thermal energy, its temperature decreases, the final temperature is lower than the initial temperature, so \(ΔT<0 \) and \(q\) is negative.
Example \(\PageIndex{1}\): Measuring Heat
A flask containing \(8.0 \times 10^2\; g\) of water is heated, and the temperature of the water increases from \(21\, °C\) to \(85\, °C\). How much heat did the water absorb?
Solution
To answer this question, consider these factors:
- the specific heat of the substance being heated (in this case, water)
- the amount of substance being heated (in this case, 800 g)
- the magnitude of the temperature change (in this case, from 21 °C to 85 °C).
The specific heat of water is 4.184 J/g °C (Table \(\PageIndex{1}\)), so to heat 1 g of water by 1 °C requires 4.184 J. We note that since 4.184 J is required to heat 1 g of water by 1 °C, we will need 800 times as much to heat 800 g of water by 1 °C. Finally, we observe that since 4.184 J are required to heat 1 g of water by 1 °C, we will need 64 times as much to heat it by 64 °C (that is, from 21 °C to 85 °C).
This can be summarized using Equation \ref{12.3.8}:
\[\begin{align*} q&=mc_sΔT \nonumber \\[4pt] &= m c_s (T_\ce{final}−T_\ce{initial}) \\[4pt]
&=\mathrm{(4.184\:J/\cancel{g}°C)×(800\:\cancel{g})×(85−21)°C} \\[4pt]
&=\mathrm{(4.184\:J/\cancel{g}°\cancel{C})×(800\:\cancel{g})×(64)°\cancel{C}} \\[4pt]
&=\mathrm{210,000\: J(=210\: kJ)} \nonumber \end{align*} \]
Because the temperature increased, the water absorbed heat and \(q\) is positive.
Exercise \(\PageIndex{1}\)
How much heat, in joules, must be added to a \(5.00 \times 10^2 \;g\) iron skillet to increase its temperature from 25 °C to 250 °C? The specific heat of iron is 0.451 J/g °C.
Answer-
\(5.07 \times 10^4\; J\)
Note that the relationship between heat, specific heat, mass, and temperature change can be used to determine any of these quantities (not just heat) if the other three are known or can be deduced.
Example \(\PageIndex{2}\): Determining Other Quantities
A piece of unknown metal weighs 348 g. When the metal piece absorbs 6.64 kJ of heat, its temperature increases from 22.4 °C to 43.6 °C. Determine the specific heat of this metal (which might provide a clue to its identity).
Solution
Since mass, heat, and temperature change are known for this metal, we can determine its specific heat using Equation \ref{12.3.8}:
\[\begin{align*} q&=m c_s \Delta T &=m c_s (T_{final}−T_{initial}) \end{align*}\]
Substituting the known values:
\[6,640\; J=(348\; g) c_s (43.6 − 22.4)\; °C \nonumber\]
Solving:
\[c=\dfrac{6,640\; J}{(348\; g)(21.2°C)} =0.900\; J/g\; °C \nonumber\]
Comparing this value with the values in Table \(\PageIndex{1}\), this value matches the specific heat of aluminum, which suggests that the unknown metal may be aluminum.
Exercise \(\PageIndex{2}\)
A piece of unknown metal weighs 217 g. When the metal piece absorbs 1.43 kJ of heat, its temperature increases from 24.5 °C to 39.1 °C. Determine the specific heat of this metal, and predict its identity.
- Answer
-
\(c = 0.45 \;J/g \;°C\); the metal is likely to be iron from checking Table \(\PageIndex{1}\).
Example \(\PageIndex{3}\): Solar Heating
A home solar energy storage unit uses 400 L of water for storing thermal energy. On a sunny day, the initial temperature of the water is 22.0°C. During the course of the day, the temperature of the water rises to 38.0°C as it circulates through the water wall. How much energy has been stored in the water? (The density of water at 22.0°C is 0.998 g/mL.)
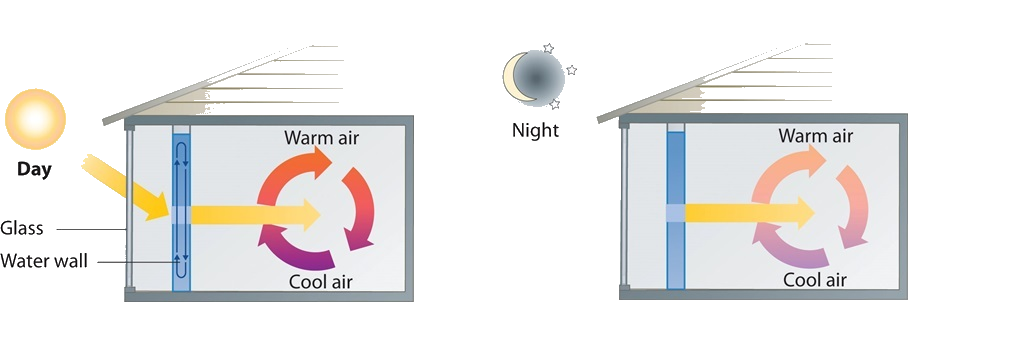
Given: volume and density of water and initial and final temperatures
Asked for: amount of energy stored
Strategy:
- Use the density of water at 22.0°C to obtain the mass of water (m) that corresponds to 400 L of water. Then compute \(ΔT\) for the water.
- Determine the amount of heat absorbed by substituting values for \(m\), \(c_s\), and \(ΔT\) into Equation \ref{12.3.1}.
Solution:
A The mass of water is
\[ mass \; of \; H_{2}O=400 \; \cancel{L}\left ( \dfrac{1000 \; \cancel{mL}}{1 \; \cancel{L}} \right ) \left ( \dfrac{0.998 \; g}{1 \; \cancel{mL}} \right ) = 3.99\times 10^{5}g\; H_{2}O \nonumber \]
The temperature change (ΔT) is 38.0°C − 22.0°C = +16.0°C.
B From Table \(\PageIndex{1}\), the specific heat of water is 4.184 J/(g•°C). From Equation \ref{12.3.8}, the heat absorbed by the water is thus
\[ q=mc_s\Delta T=\left ( 3.99 \times 10^{5} \; \cancel{g} \right )\left ( \dfrac{4.184 \; J}{\cancel{g}\cdot \bcancel{^{o}C}} \right ) \left ( 16.0 \; \bcancel{^{o}C} \right ) = 2.67 \times 10^{7}J = 2.67 \times 10^{4}kJ \nonumber \]
Both q and ΔT are positive, consistent with the fact that the water has absorbed energy.
Exercise \(\PageIndex{3}\): Solar Heating
Some solar energy devices used in homes circulate air over a bed of rocks that absorb thermal energy from the sun. If a house uses a solar heating system that contains 2500 kg of sandstone rocks, what amount of energy is stored if the temperature of the rocks increases from 20.0°C to 34.5°C during the day? Assume that the specific heat of sandstone is the same as that of quartz (SiO2) in Table \(\PageIndex{1}\).
- Answer
-
\(2.7 × 10^4\, kJ \)
Even though the mass of sandstone is more than six times the mass of the water in Example \(\PageIndex{1}\), the amount of thermal energy stored is the same to two significant figures.
Heat "Flow" to Thermal Equilibrium
When two objects at different temperatures are placed in contact, heat flows from the warmer object to the cooler one until the temperature of both objects is the same. The law of conservation of energy says that the total energy cannot change during this process:
\[q_{cold} + q_{hot} = 0 \label{12.3.9}\]
The equation implies that the amount of heat that flows from a warmer object is the same as the amount of heat that flows into a cooler object. Because the direction of heat flow is opposite for the two objects, the sign of the heat flow values must be opposite:
\[q_{cold} = −q_{hot} \label{12.3.10}\]
Thus heat is conserved in any such process, consistent with the law of conservation of energy.
The amount of heat lost by a warmer object equals the amount of heat gained by a cooler object.
Substituting for \(q\) from Equation \(\ref{12.3.8}\) gives
\[ \left [ mc_s \Delta T \right ] _{cold} + \left [ mc_s \Delta T \right ] _{hot}=0 \label{12.3.11} \nonumber \]
which can be rearranged to give
\[ \left [ mc_s \Delta T \right ] _{cold} = - \left [ mc_s \Delta T \right ] _{hot} \label{12.3.12} \]
When two objects initially at different temperatures are placed in contact, we can use Equation \(\ref{12.3.12}\) to calculate the final temperature if we know the chemical composition and mass of the objects.
Example \(\PageIndex{4}\): Thermal Equilibration of Copper and Water
If a 30.0 g piece of copper pipe at 80.0°C is placed in 100.0 g of water at 27.0°C, what is the final temperature? Assume that no heat is transferred to the surroundings.
Given: mass and initial temperature of two objects
Asked for: final temperature
Strategy: Using Equation \(\ref{12.3.12}\) and writing \(ΔT= T_{final} − T_{initial}\) for both the copper and the water, substitute the appropriate values of \(m\), \(c_s\), and \(T_{initial}\) into the equation and solve for \(T_{final}\).
Solution
We can adapt Equation \(\ref{12.3.12}\) to solve this problem, remembering that \(ΔT= T_{final} − T_{initial}\):\[ \left [ mc_s \left (T_{final} - T_{initial} \right ) \right ] _{Cu} + \left [ mc_s \left (T_{final} - T_{initial} \right ) \right ] _{H_{2}O} =0 \nonumber \]
Substituting the data provided in the problem and Table \(\PageIndex{1}\) gives
\[\begin{align*} \left (30 \; g \right ) (0.385 \; J/ (g °C) ) (T_{final} - 80°C) + (100\;g) (4.184 \; J/ (g °C) ) (T_{final} - 27.0°C ) &= 0 \nonumber \\[4pt] T_{final}\left ( 11.6 \; J/ ^{o}C \right ) -924 \; J + T_{final}\left ( 418.4 \; J/ ^{o}C \right ) -11,300 \; J &= 0 \\[4pt] T_{final}\left ( 430 \; J/\left ( g\cdot ^{o}C \right ) \right ) &= 12,224 \; J \nonumber \\[4pt] T_{final} &= 28.4 \; ^{o}C \end{align*} \]
Exercise \(\PageIndex{4A}\): Thermal Equilibration of Gold and Water
If a 14.0 g chunk of gold at 20.0°C is dropped into 25.0 g of water at 80.0°C, what is the final temperature if no heat is transferred to the surroundings?
- Answer
-
80.0°C
Exercise \(\PageIndex{4B}\): Thermal Equilibration of Aluminum and Water
A 28.0 g chunk of aluminum is dropped into 100.0 g of water with an initial temperature of 20.0°C. If the final temperature of the water is 24.0°C, what was the initial temperature of the aluminum? (Assume that no heat is transferred to the surroundings.)
- Answer
-
90.6°C
Measuring Heat "Flow"
One technique we can use to measure the amount of heat involved in a chemical or physical process is known as calorimetry. Calorimetry is used to measure amounts of heat transferred to or from a substance. To do so, the heat is exchanged with a calibrated object (calorimeter). The change in temperature of the measuring part of the calorimeter is converted into the amount of heat (since the previous calibration was used to establish its heat capacity). The measurement of heat transfer using this approach requires the definition of a system (the substance or substances undergoing the chemical or physical change) and its surroundings (the other components of the measurement apparatus that serve to either provide heat to the system or absorb heat from the system). Knowledge of the heat capacity of the surroundings, and careful measurements of the masses of the system and surroundings and their temperatures before and after the process allows one to calculate the heat transferred as described in this section.
A calorimeter is a device used to measure the amount of heat involved in a chemical or physical process.
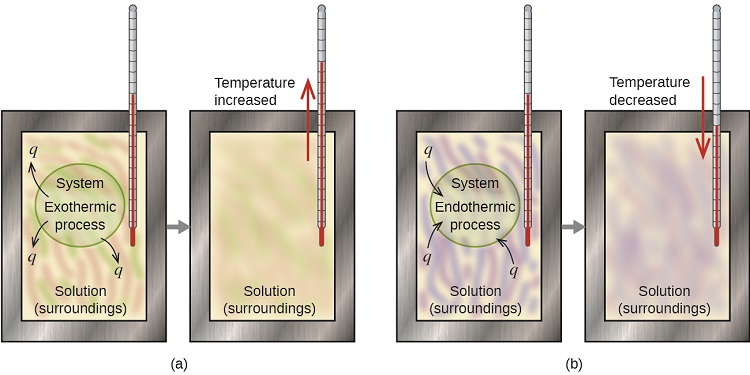
The thermal energy change accompanying a chemical reaction is responsible for the change in temperature that takes place in a calorimeter. If the reaction releases heat (qrxn < 0), then heat is absorbed by the calorimeter (qcalorimeter > 0) and its temperature increases. Conversely, if the reaction absorbs heat (qrxn > 0), then heat is transferred from the calorimeter to the system (qcalorimeter < 0) and the temperature of the calorimeter decreases. In both cases, the amount of heat absorbed or released by the calorimeter is equal in magnitude and opposite in sign to the amount of heat produced or consumed by the reaction. The heat capacity of the calorimeter or of the reaction mixture may be used to calculate the amount of heat released or absorbed by the chemical reaction. The amount of heat released or absorbed per gram or mole of reactant can then be calculated from the mass of the reactants.
The amount of heat absorbed or released by the calorimeter is equal in magnitude and opposite in sign to the amount of heat produced or consumed by the reaction.
Constant-Pressure Calorimetry
Because \(ΔH\) is defined as the heat flow at constant pressure, measurements made using a constant-pressure calorimeter (a device used to measure enthalpy changes in chemical processes at constant pressure) give \(ΔH\) values directly. This device is particularly well suited to studying reactions carried out in solution at a constant atmospheric pressure. A “student” version, called a coffee-cup calorimeter (Figure \(\PageIndex{3}\)), is often encountered in general chemistry laboratories. Commercial calorimeters operate on the same principle, but they can be used with smaller volumes of solution, have better thermal insulation, and can detect a change in temperature as small as several millionths of a degree (10−6 °C).
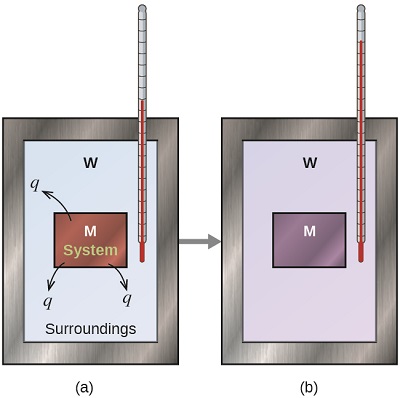
Before we practice calorimetry problems involving chemical reactions, consider a simpler example that illustrates the core idea behind calorimetry. Suppose we initially have a high-temperature substance, such as a hot piece of metal (M), and a low-temperature substance, such as cool water (W). If we place the metal in the water, heat will flow from M to W. The temperature of M will decrease, and the temperature of W will increase, until the two substances have the same temperature—that is, when they reach thermal equilibrium. If this occurs in a calorimeter, ideally all of this heat transfer occurs between the two substances, with no heat gained or lost by either the calorimeter or the calorimeter’s surroundings. Under these ideal circumstances, the net heat change is zero:
\[q_\mathrm{\,substance\: M} + q_\mathrm{\,substance\: W}=0 \label{12.3.13}\]
This relationship can be rearranged to show that the heat gained by substance M is equal to the heat lost by substance W:
\[q_\mathrm{\,substance\: M}=-q_\mathrm{\,substance\: W} \label{12.3.14}\]
The magnitude of the heat (change) is therefore the same for both substances, and the negative sign merely shows that \(q_{substance\; M}\) and \(q_{substance\; W}\) are opposite in direction of heat flow (gain or loss) but does not indicate the arithmetic sign of either q value (that is determined by whether the matter in question gains or loses heat, per definition). In the specific situation described, \(q_{substance\, M}\) is a negative value and qsubstance W is positive, since heat is transferred from M to W.
Example \(\PageIndex{5}\): Heat between Substances at Different Temperatures
A 360-g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 mL of water at 24.0 °C. The final temperature of the water was measured as 42.7 °C. Calculate the initial temperature of the piece of rebar. Assume the specific heat of steel is approximately the same as that for iron (Table T4), and that all heat transfer occurs between the rebar and the water (there is no heat exchange with the surroundings).
Solution
The temperature of the water increases from 24.0 °C to 42.7 °C, so the water absorbs heat. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all heat transfer was between the rebar and the water, with no heat “lost” to the surroundings, then heat given off by rebar = −heat taken in by water, or:
Since we know how heat is related to other measurable quantities, we have:
Letting f = final and i = initial, in expanded form, this becomes:
\[ c_\ce{rebar}×m_\ce{rebar}×(T_\mathrm{f,rebar}−T_\mathrm{i,rebar})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber\]
The density of water is 1.0 g/mL, so 425 mL of water = 425 g. Noting that the final temperature of both the rebar and water is 42.7 °C, substituting known values yields:
\[ \mathrm{(0.449\:J/g\: °C)(360g)(42.7°C−\mathit T_\mathrm{i,rebar})=-(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)} \nonumber\]
\[\mathrm{\mathit T_{i,rebar}=\dfrac{(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)}{(0.449\:J/g\: °C)(360\:g)}+42.7°C} \nonumber\]
Solving this gives \(T_{i,rebar}\)= 248 °C, so the initial temperature of the rebar was 248 °C.
Exercise \(\PageIndex{5A}\)
A 248-g piece of copper is dropped into 390 mL of water at 22.6 °C. The final temperature of the water was measured as 39.9 °C. Calculate the initial temperature of the piece of copper. Assume that all heat transfer occurs between the copper and the water.
- Answer
-
The initial temperature of the copper was 335.6 °C.
Exercise \(\PageIndex{5B}\)
A 248-g piece of copper initially at 314 °C is dropped into 390 mL of water initially at 22.6 °C. Assuming that all heat transfer occurs between the copper and the water, calculate the final temperature.
- Answer
-
The final temperature (reached by both copper and water) is 38.8 °C.
This method can also be used to determine other quantities, such as the specific heat of an unknown metal.
Example \(\PageIndex{6}\): Identifying a Metal by Measuring Specific Heat
A 59.7 g piece of metal that had been submerged in boiling water was quickly transferred into 60.0 mL of water initially at 22.0 °C. The final temperature is 28.5 °C. Use these data to determine the specific heat of the metal. Use this result to identify the metal.
Solution
Assuming perfect heat transfer, heat given off by metal = −heat taken in by water, or:
In expanded form, this is:
\[c_\ce{metal}×m_\ce{metal}×(T_\mathrm{f,metal}−T_\mathrm{i, metal})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber\]
Noting that since the metal was submerged in boiling water, its initial temperature was 100.0 °C; and that for water, 60.0 mL = 60.0 g; we have:
\[\mathrm{(\mathit c_{metal})(59.7\:g)(28.5°C−100.0°C)=−(4.18\:J/g\: °C)(60.0\:g)(28.5°C−22.0°C)} \nonumber\]
Solving this:
\[\mathrm{\mathit c_{metal}=\dfrac{−(4.184\:J/g\: °C)(60.0\:g)(6.5°C)}{(59.7\:g)(−71.5°C)}=0.38\:J/g\: °C} \nonumber \]
Comparing this with values in Table T4, our experimental specific heat is closest to the value for copper (0.39 J/g °C), so we identify the metal as copper.
Exercise \(\PageIndex{6}\)
A 92.9-g piece of a silver/gray metal is heated to 178.0 °C, and then quickly transferred into 75.0 mL of water initially at 24.0 °C. After 5 minutes, both the metal and the water have reached the same temperature: 29.7 °C. Determine the specific heat and the identity of the metal. (Note: You should find that the specific heat is close to that of two different metals. Explain how you can confidently determine the identity of the metal).
- Answer
-
\(c_{metal}= 0.13 \;J/g\; °C\)
This specific heat is close to that of either gold or lead. It would be difficult to determine which metal this was based solely on the numerical values. However, the observation that the metal is silver/gray in addition to the value for the specific heat indicates that the metal is lead.
When we use calorimetry to determine the heat involved in a chemical reaction, the same principles we have been discussing apply. The amount of heat absorbed by the calorimeter is often small enough that we can neglect it (though not for highly accurate measurements, as discussed later), and the calorimeter minimizes energy exchange with the surroundings. Because energy is neither created nor destroyed during a chemical reaction, there is no overall energy change during the reaction. The heat produced or consumed in the reaction (the “system”), qreaction, plus the heat absorbed or lost by the solution (the “surroundings”), qsolution, must add up to zero:
This means that the amount of heat produced or consumed in the reaction equals the amount of heat absorbed or lost by the solution:
\[q_\ce{reaction}=−q_\ce{solution} \label{12.3.16}\]
This concept lies at the heart of all calorimetry problems and calculations. Because the heat released or absorbed at constant pressure is equal to ΔH, the relationship between heat and ΔHrxn is
\[ \Delta H_{rxn}=q_{rxn}=-q_{calorimater}=-mc_s \Delta T \label{12.3.17} \]
The use of a constant-pressure calorimeter is illustrated in Example \(\PageIndex{7}\).
Example \(\PageIndex{7}\): Heat of Solution
When 5.03 g of solid potassium hydroxide are dissolved in 100.0 mL of distilled water in a coffee-cup calorimeter, the temperature of the liquid increases from 23.0°C to 34.7°C. The density of water in this temperature range averages 0.9969 g/cm3. What is \(ΔH_{soln}\) (in kilojoules per mole)? Assume that the calorimeter absorbs a negligible amount of heat and, because of the large volume of water, the specific heat of the solution is the same as the specific heat of pure water.
Given: mass of substance, volume of solvent, and initial and final temperatures
Asked for: ΔHsoln
Strategy:
- Calculate the mass of the solution from its volume and density and calculate the temperature change of the solution.
- Find the heat flow that accompanies the dissolution reaction by substituting the appropriate values into Equation \ref{12.3.1}.
- Use the molar mass of \(\ce{KOH}\) to calculate ΔHsoln.
Solution:
A To calculate ΔHsoln, we must first determine the amount of heat released in the calorimetry experiment. The mass of the solution is
\[ \left (100.0 \; \cancel{mL}\; \ce{H2O} \right ) \left ( 0.9969 \; g/ \cancel{mL} \right )+ 5.03 \; g \; KOH=104.72 \; g \nonumber\]
The temperature change is (34.7°C − 23.0°C) = +11.7°C.
B Because the solution is not very concentrated (approximately 0.9 M), we assume that the specific heat of the solution is the same as that of water. The heat flow that accompanies dissolution is thus
\[ \begin{align*} q_{calorimater} &= mc_s \Delta T \nonumber \\[4pt] &= \left ( 104.72 \; \cancel{g} \right ) \left ( \dfrac{4.184 \; J}{\cancel{g}\cdot \bcancel{^{o}C}} \right )\left ( 11.7 \; \bcancel{^{o}C} \right ) \nonumber \\[4pt] &= 5130 \; J \\[4pt] &=5.13 \; kJ \end{align*} \]
The temperature of the solution increased because heat was absorbed by the solution (q > 0). Where did this heat come from? It was released by KOH dissolving in water. From Equation \ref{12.3.1}, we see that
\[ΔH_{rxn} = −q_{calorimeter} = −5.13\, kJ \nonumber\]
This experiment tells us that dissolving 5.03 g of \(\ce{KOH}\) in water is accompanied by the release of 5.13 kJ of energy. Because the temperature of the solution increased, the dissolution of KOH in water must be exothermic.
C The last step is to use the molar mass of \(\ce{KOH}\) to calculate \(ΔH_{soln}\) - the heat associated when dissolving 1 mol of \(\ce{KOH}\):
\[ \begin{align*} \Delta H_{soln} &= \left ( \dfrac{5.13 \; kJ}{5.03 \; \cancel{g}} \right )\left ( \dfrac{56.11 \; \cancel{g}}{1 \; mol} \right ) \nonumber \\[4pt] &= -57.2 \; kJ/mol\end{align*} \]
Exercise \(\PageIndex{7}\): Heat of Dissolving
A coffee-cup calorimeter contains 50.0 mL of distilled water at 22.7°C. Solid ammonium bromide (3.14 g) is added and the solution is stirred, giving a final temperature of 20.3°C. Using the same assumptions as in Example \(\PageIndex{7}\), find \(ΔH_{soln}\) for NH4Br (in kilojoules per mole).
- Answer
-
16.6 kJ/mol
Constant-Volume Calorimetry
Constant-pressure calorimeters are not very well suited for studying reactions in which one or more of the reactants is a gas, such as a combustion reaction. The enthalpy changes that accompany combustion reactions are therefore measured using a constant-volume calorimeter, such as the bomb calorimeter (A device used to measure energy changes in chemical processes. shown schematically in Figure \(\PageIndex{4}\)). The reactant is placed in a steel cup inside a steel vessel with a fixed volume (the “bomb”). The bomb is then sealed, filled with excess oxygen gas, and placed inside an insulated container that holds a known amount of water. Because combustion reactions are exothermic, the temperature of the bath and the calorimeter increases during combustion. If the heat capacity of the bomb and the mass of water are known, the heat released can be calculated.
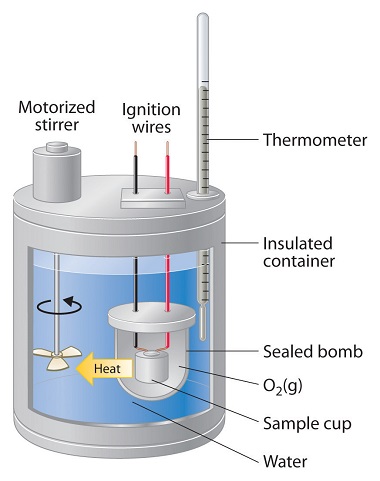
Because the volume of the system (the inside of the bomb) is fixed, the combustion reaction occurs under conditions in which the volume, but not the pressure, is constant. The heat released by a reaction carried out at constant volume is identical to the change in internal energy (\(ΔU\)) rather than the enthalpy change (ΔH); ΔU is related to ΔH by an expression that depends on the change in the number of moles of gas during the reaction. The difference between the heat flow measured at constant volume and the enthalpy change is usually quite small, however (on the order of a few percent). Assuming that \(ΔU < ΔH\), the relationship between the measured temperature change and ΔHcomb is given in Equation \ref{12.3.18}, where Cbomb is the total heat capacity of the steel bomb and the water surrounding it
\[ \Delta H_{comb} < q_{comb} = q_{calorimater} = C_{bomb} \Delta T \label{12.3.18}\]
To measure the heat capacity of the calorimeter, we first burn a carefully weighed mass of a standard compound whose enthalpy of combustion is accurately known. Benzoic acid (C6H5CO2H) is often used for this purpose because it is a crystalline solid that can be obtained in high purity. The combustion of benzoic acid in a bomb calorimeter releases 26.38 kJ of heat per gram (i.e., its ΔHcomb = −26.38 kJ/g). This value and the measured increase in temperature of the calorimeter can be used to determine Cbomb. The use of a bomb calorimeter to measure the ΔHcomb of a substance is illustrated in Example \(\PageIndex{8}\).
Video \(\PageIndex{1}\): Video of view how a bomb calorimeter is prepared for action.
Example \(\PageIndex{8}\): Combustion of Glucose
The combustion of 0.579 g of benzoic acid in a bomb calorimeter caused a 2.08°C increase in the temperature of the calorimeter. The chamber was then emptied and recharged with 1.732 g of glucose and excess oxygen. Ignition of the glucose resulted in a temperature increase of 3.64°C. What is the ΔHcomb of glucose?
Given: mass and ΔT for combustion of standard and sample
Asked for: ΔHcomb of glucose
Strategy:
- Calculate the value of qrxn for benzoic acid by multiplying the mass of benzoic acid by its ΔHcomb. Then use Equation \ref{12.3.1} to determine the heat capacity of the calorimeter (Cbomb) from qcomb and ΔT.
- Calculate the amount of heat released during the combustion of glucose by multiplying the heat capacity of the bomb by the temperature change. Determine the ΔHcomb of glucose by multiplying the amount of heat released per gram by the molar mass of glucose.
Solution:
The first step is to use Equation \ref{12.3.1} and the information obtained from the combustion of benzoic acid to calculate Cbomb. We are given ΔT, and we can calculate \(q_{comb}\) from the mass of benzoic acid:
\[ q_{comb} = \left ( 0.579 \; \cancel{g} \right )\left ( -26.38 \; kJ/\cancel{g} \right ) = - 15.3 \; kJ \nonumber \]
From Equation \ref{12.3.1},
\[ -C_{bomb} = \dfrac{q_{comb}}{\Delta T} = \dfrac{-15.3 \; kJ}{2.08 \; ^{o}C} =- 7.34 \; kJ/^{o}C \nonumber \]
B According to the strategy, we can now use the heat capacity of the bomb to calculate the amount of heat released during the combustion of glucose:
\[ q_{comb}=-C_{bomb}\Delta T = \left ( -7.34 \; kJ/^{o}C \right )\left ( 3.64 \; ^{o}C \right )=- 26.7 \; kJ \nonumber\]
Because the combustion of 1.732 g of glucose released 26.7 kJ of energy, the ΔHcomb of glucose is
\[ \Delta H_{comb}=\left ( \dfrac{-26.7 \; kJ}{1.732 \; \cancel{g}} \right )\left ( \dfrac{180.16 \; \cancel{g}}{mol} \right )=-2780 \; kJ/mol =2.78 \times 10^{3} \; kJ/mol \nonumber\]
This result is in good agreement (< 1% error) with the value of \(ΔH_{comb} = −2803\, kJ/mol\) that calculated using enthalpies of formation.
Exercise \(\PageIndex{8}\): Combustion of Benzoic Acid
When 2.123 g of benzoic acid is ignited in a bomb calorimeter, a temperature increase of 4.75°C is observed. When 1.932 g of methylhydrazine (CH3NHNH2) is ignited in the same calorimeter, the temperature increase is 4.64°C. Calculate the ΔHcomb of methylhydrazine, the fuel used in the maneuvering jets of the US space shuttle.
- Answer
-
−1.30 × 103 kJ/mol
Summary
Calorimetry measures enthalpy changes during chemical processes, where the magnitude of the temperature change depends on the amount of heat released or absorbed and on the heat capacity of the system. Calorimetry is the set of techniques used to measure enthalpy changes during chemical processes. It uses devices called calorimeters, which measure the change in temperature when a chemical reaction is carried out. The magnitude of the temperature change depends on the amount of heat released or absorbed and on the heat capacity of the system. The heat capacity (C) of an object is the amount of energy needed to raise its temperature by 1°C; its units are joules per degree Celsius. The specific heat (\(c_s\)) of a substance is the amount of energy needed to raise the temperature of 1 g of the substance by 1°C, and the molar heat capacity (\(c_p\)) is the amount of energy needed to raise the temperature of 1 mol of a substance by 1°C. Liquid water has one of the highest specific heats known. Heat flow measurements can be made with either a constant-pressure calorimeter, which gives \(ΔH\) values directly, or a bomb calorimeter, which operates at constant volume and is particularly useful for measuring enthalpies of combustion.
Thermal energy itself cannot be measured easily, but the temperature change caused by the flow of thermal energy between objects or substances can be measured. Calorimetry describes a set of techniques employed to measure enthalpy changes in chemical processes using devices called calorimeters. To have any meaning, the quantity that is actually measured in a calorimetric experiment, the change in the temperature of the device, must be related to the heat evolved or consumed in a chemical reaction. We begin this section by explaining how the flow of thermal energy affects the temperature of an object.
Contributors and Attributions
- Anonymous
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

