4.4: Phase Equilibrium in Solutions - Volatile Solutes
- Page ID
- 43417
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- To understand the relationship among temperature, pressure, and solubility.
- The understand that the solubility of a solid may increase or decrease with increasing temperature,
- To understand that the solubility of a gas decreases with an increase in temperature and a decrease in pressure.
- Describe the physical reasons that a binary liquid solution might exhibit non-ideal behavior
Vapor Pressure of Solutions and Raoult’s Law For Volatile Solutes
When a solute is volatile, meaning that it has a measurable vapor pressure, we can still use Raoult’s law. In this case, we calculate the vapor pressure of each component separately. The total vapor pressure of the solution (\(P_{tot}\)) is the sum of the vapor pressures of the components:
\[\begin{align} P_{tot} &= P_A+P_B \label{13.5.4a}\\[5pt] &=\chi_AP^0_A+\chi_BP^0_B \label{13.5.4} \end{align}\]
Because \(\chi_B = 1 − \chi_A\) for a two-component system,
\[P_{tot}=\chi_AP^0_A+(1−\chi_A)P^0_B \label{13.5.5}\]
Thus we need to specify the mole fraction of only one of the components in a two-component system. Consider, for example, the vapor pressure of solutions of benzene and toluene of various compositions. At 20°C, the vapor pressures of pure benzene and toluene are 74.7 and 22.3 mmHg, respectively. The vapor pressure of benzene in a benzene–toluene solution is
and the vapor pressure of toluene in the solution is
\[P{C_6H_5CH_3}=\chi_{C_6H_5CH_3}P^0_{C_6H_5CH3} \label{13.5.7}\]
Equations \(\ref{13.5.6}\) and \(\ref{13.5.7}\) are both in the form of the equation for a straight line: \(y = mx + b\), where \(b = 0\). Plots of the vapor pressures of both components versus the mole fractions are therefore straight lines that pass through the origin, as shown in Figure \(\PageIndex{3}\). Furthermore, a plot of the total vapor pressure of the solution versus the mole fraction is a straight line that represents the sum of the vapor pressures of the pure components. Thus the vapor pressure of the solution is always greater than the vapor pressure of either component.
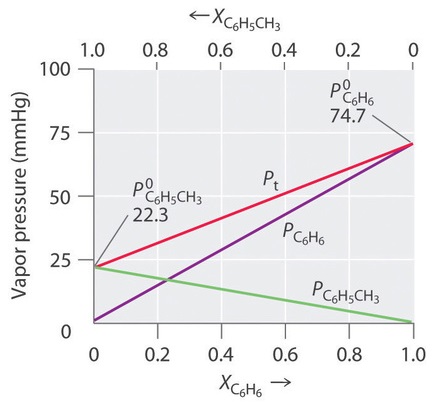
A solution of two volatile components that behaves like the solution in Figure \(\PageIndex{3}\), which is defined as a solution that obeys Raoult’s law. Like an ideal gas, an ideal solution is a hypothetical system whose properties can be described in terms of a simple model. Mixtures of benzene and toluene approximate an ideal solution because the intermolecular forces in the two pure liquids are almost identical in both kind and magnitude. Consequently, the change in enthalpy on solution formation is essentially zero (\(ΔH_{soln} ≈ 0\)), which is one of the defining characteristics of an ideal solution.
Ideal solutions and ideal gases are both simple models that ignore intermolecular interactions.
For each system, compare the intermolecular interactions in the pure liquids and in the solution to decide whether the vapor pressure will be greater than that predicted by Raoult’s law (positive deviation), approximately equal to that predicted by Raoult’s law (an ideal solution), or less than the pressure predicted by Raoult’s law (negative deviation).
- cyclohexane and ethanol
- methanol and acetone
- n-hexane and isooctane (2,2,4-trimethylpentane)
Given: identity of pure liquids
Asked for: predicted deviation from Raoult’s law (Equation \ref{13.5.4})
Strategy:
Identify whether each liquid is polar or nonpolar, and then predict the type of intermolecular interactions that occur in solution.
Solution:
- Liquid ethanol contains an extensive hydrogen bonding network, and cyclohexane is nonpolar. Because the cyclohexane molecules cannot interact favorably with the polar ethanol molecules, they will disrupt the hydrogen bonding. Hence the A–B interactions will be weaker than the A–A and B–B interactions, leading to a higher vapor pressure than predicted by Raoult’s law (a positive deviation).
- Methanol contains an extensive hydrogen bonding network, but in this case the polar acetone molecules create A–B interactions that are stronger than the A–A or B–B interactions, leading to a negative enthalpy of solution and a lower vapor pressure than predicted by Raoult’s law (a negative deviation).
- Hexane and isooctane are both nonpolar molecules (isooctane actually has a very small dipole moment, but it is so small that it can be ignored). Hence the predominant intermolecular forces in both liquids are London dispersion forces. We expect the A–B interactions to be comparable in strength to the A–A and B–B interactions, leading to a vapor pressure in good agreement with that predicted by Raoult’s law (an ideal solution).
For each system, compare the intermolecular interactions in the pure liquids with those in the solution to decide whether the vapor pressure will be greater than that predicted by Raoult’s law (positive deviation), approximately equal to that predicted by Raoult’s law (an ideal solution), or less than the pressure predicted by Raoult’s law (negative deviation):
- benzene and n-hexane
- ethylene glycol and \(\ce{CCl_4}\)
- acetic acid and n-propanol
- Answer a
-
approximately equal
- Answer b
-
positive deviation (vapor pressure greater than predicted)
- Answer c
-
negative deviation (vapor pressure less than predicted)
Ideal vs. Real Solutions
Another solution whose components follow Raoult's law quite closely is a solution of hexane \(\ce{C6H14}\) and heptane \(\ce{C7H16}\). The total vapor pressure of this solution varies in a straight-line manner with the mole fraction composition of the mixture (Figure \(\PageIndex{2}\)). Note that the mole fraction scales at the top and bottom run in opposite directions, since by definition,
\[\chi_{hexane} = 1 – \chi_{heptane} \nonumber\]
If this solution behaves ideally, then is the sum of the Raoult's law plots for the two pure compounds (i.e., Equation \ref{13.5.4a}):
\[P_{total} = P_{ heptane } + P_{ hexane } \nonumber\]
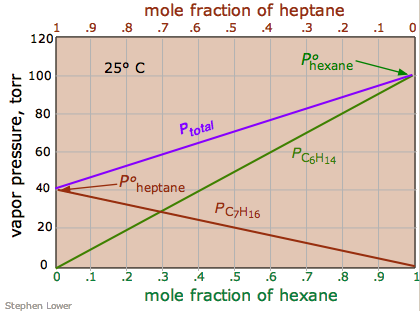
An ideal solution is one whose vapor pressure follows Raoult's law throughout its range of compositions. Experience has shown solutions that approximate ideal behavior are composed of molecules having very similar structures. Thus hexane and heptane are both linear hydrocarbons that differ only by a single –CH2 group.

Most real solutions, however, do not obey Raoult’s law precisely, just as most real gases do not obey the ideal gas law exactly. Real solutions generally deviate from Raoult’s law because the intermolecular interactions between the two components A and B differ. We can distinguish between two general kinds of behavior, depending on whether the intermolecular interactions between molecules A and B are stronger or weaker than the A–A and B–B interactions in the pure components.
- If the A–B interactions are stronger than the A–A and B–B interactions, each component of the solution exhibits a lower vapor pressure than expected for an ideal solution, as does the solution as a whole. The favorable A–B interactions effectively stabilize the solution compared with the vapor. This kind of behavior is called a negative deviation from Raoult’s law. Systems stabilized by hydrogen bonding between two molecules, such as acetone and ethanol, exhibit negative deviations from Raoult’s law. The chloroform-acetone system (Figure \(\PageIndex{3}\)) is a good example.
- Conversely, if the A–B interactions are weaker than the A–A and B–B interactions yet the entropy increase is enough to allow the solution to form, both A and B have an increased tendency to escape from the solution into the vapor phase. The result is a higher vapor pressure than expected for an ideal solution, producing a positive deviation from Raoult’s law. In a solution of \(\ce{CCl_4}\) and methanol, for example, the nonpolar \(\ce{CCl_4}\) molecules interrupt the extensive hydrogen bonding network in methanol, and the lighter methanol molecules have weaker London dispersion forces than the heavier \(\ce{CCl_4}\) molecules. Consequently, solutions of \(\ce{CCl_4}\) and methanol exhibit positive deviations from Raoult’s law. It should not be surprising molecules as different as benzene and \(CS_2\) should interact more strongly with their own kind, hence the positive deviation in Figure \(\PageIndex{3}\)).
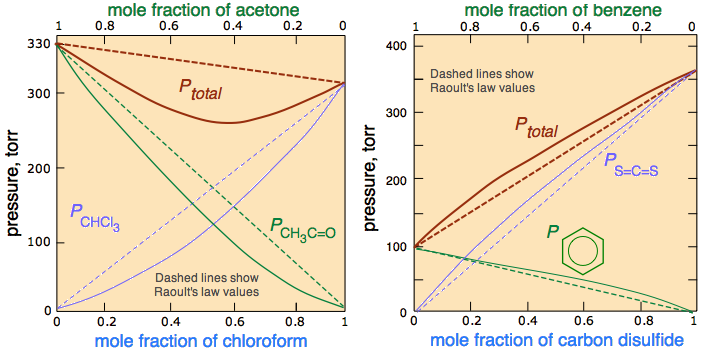
The ideal solution differs in a fundamental way from the definition of an ideal gas, defined as a hypothetical substance that follows the ideal gas law. The kinetic molecular theory that explains ideal gas behavior assumes that the molecules occupy no space and that intermolecular attractions are totally absent.
The definition of an ideal gas is clearly inapplicable to liquids, whose volumes directly reflect the volumes of their component molecules. And of course, the very ability of the molecules to form a condensed phase is due to the attractive forces between the molecules. So the most we can say about an ideal solution is that the attractions between its all of its molecules are identical — that is, A-type molecules are as strongly attracted to other A molecules as to B-type molecules. Ideal solutions are perfectly democratic: there are no favorites.
You will recall that all gases approach ideal behavior as their pressures approach zero. In the same way, as the mole fraction of either component approaches unity, the behavior of the solution approaches ideality. This is a simple consequence of the fact that at these limits, each molecule is surrounded mainly by its own kind, and the few A-B interactions will have little effect. Raoult's law is therefore a limiting law:
\[P_i = \lim_{x_i \rightarrow 0} P^o \chi_i\]
it gives the partial pressure of a substance in equilibrium with the solution more and more closely as the mole fraction of that substance approaches unity.
Effect of Pressure on the Solubility of Gases - Henry’s Law
External pressure has very little effect on the solubility of liquids and solids. In contrast, the solubility of gases increases as the partial pressure of the gas above a solution increases. This point is illustrated in Figure \(\PageIndex{4}\), which shows the effect of increased pressure on the dynamic equilibrium that is established between the dissolved gas molecules in solution and the molecules in the gas phase above the solution. Because the concentration of molecules in the gas phase increases with increasing pressure, the concentration of dissolved gas molecules in the solution at equilibrium is also higher at higher pressures.
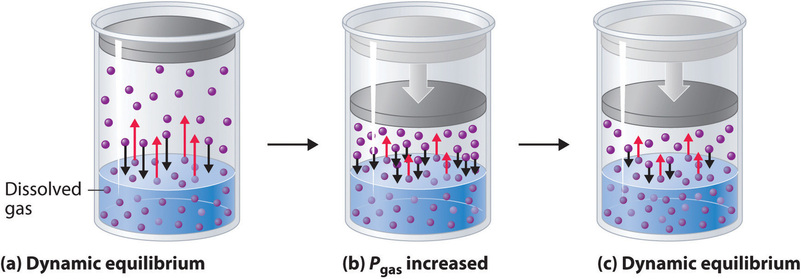
The relationship between pressure and the solubility of a gas is described quantitatively by Henry’s law, which is named for its discoverer, the English physician and chemist, William Henry (1775–1836):
\[C = k_HP \label{11.61}\]
where \(C\) is the concentration of dissolved gas at equilibrium, \(P\) is the partial pressure of the gas, and \(k_H\) is the Henry’s law constant, which must be determined experimentally for each combination of gas, solvent, and temperature.
Although the gas concentration may be expressed in any convenient units, we will use molarity exclusively. The units of the Henry’s law constant are therefore mol/(L·atm) = M/atm. Values of the Henry’s law constants for solutions of several gases in water at 20°C are listed in Table \(\PageIndex{1}\).
As the data in Table \(\PageIndex{1}\) demonstrate, the concentration of a dissolved gas in water at a given pressure depends strongly on its physical properties. For a series of related substances, London dispersion forces increase as molecular mass increases. Thus among the Group 18 elements, the Henry’s law constants increase smoothly from \(\ce{He}\) to \(\ce{Ne}\) to \(\ce{Ar}\).
| Gas | Henry’s Law Constant [mol/(L·atm)] × 10−4 |
|---|---|
| \(\ce{He}\) | 3.9 |
| \(\ce{Ne}\) | 4.7 |
| \(\ce{Ar}\) | 15 |
| \(\ce{H_2}\) | 8.1 |
| \(\ce{N_2}\) | 7.1 |
| \(\ce{O_2}\) | 14 |
| \(\ce{CO_2}\) | 392 |
Nitrogen and oxygen are the two most prominent gases in the Earth’s atmosphere and they share many similar physical properties. However, as Table \(\PageIndex{1}\) shows, \(\ce{O2}\) is twice as soluble in water as \(\ce{N2}\). Many factors contribute to solubility including the nature of the intermolecular forces at play. For a details discussion, see "The O2/N2 Ratio Gas Solubility Mystery" by Rubin Battino and Paul G. Seybold (J. Chem. Eng. Data 2011, 56, 5036–5044),
Gases that react chemically with water, such as \(\ce{HCl}\) and the other hydrogen halides, \(\ce{H2S}\), and \(\ce{NH3}\), do not obey Henry’s law; all of these gases are much more soluble than predicted by Henry’s law. For example, \(\ce{HCl}\) reacts with water to give \(\ce{H^{+}(aq)}\) and \(\ce{Cl^{-}(aq)}\), not dissolved \(\ce{HCl}\) molecules, and its dissociation into ions results in a much higher solubility than expected for a neutral molecule.
Gases that react with water do not obey Henry’s law.
Henry’s law has important applications. For example, bubbles of \(\ce{CO2}\) form as soon as a carbonated beverage is opened because the drink was bottled under \(\ce{CO2}\) at a pressure greater than 1 atm. When the bottle is opened, the pressure of \(\ce{CO2}\) above the solution drops rapidly, and some of the dissolved gas escapes from the solution as bubbles. Henry’s law also explains why scuba divers have to be careful to ascend to the surface slowly after a dive if they are breathing compressed air. At the higher pressures under water, more N2 from the air dissolves in the diver’s internal fluids. If the diver ascends too quickly, the rapid pressure change causes small bubbles of \(\ce{N2}\) to form throughout the body, a condition known as “the bends.” These bubbles can block the flow of blood through the small blood vessels, causing great pain and even proving fatal in some cases.
Due to the low Henry’s law constant for \(\ce{O_2}\) in water, the levels of dissolved oxygen in water are too low to support the energy needs of multicellular organisms, including humans. To increase the \(\ce{O_2}\) concentration in internal fluids, organisms synthesize highly soluble carrier molecules that bind \(\ce{O_2}\) reversibly. For example, human red blood cells contain a protein called hemoglobin that specifically binds \(\ce{O_2}\) and facilitates its transport from the lungs to the tissues, where it is used to oxidize food molecules to provide energy. The concentration of hemoglobin in normal blood is about 2.2 mM, and each hemoglobin molecule can bind four \(\ce{O_2}\) molecules. Although the concentration of dissolved \(\ce{O_2}\) in blood serum at 37°C (normal body temperature) is only 0.010 mM, the total dissolved \(\ce{O_2}\) concentration is 8.8 mM, almost a thousand times greater than would be possible without hemoglobin. Synthetic oxygen carriers based on fluorinated alkanes have been developed for use as an emergency replacement for whole blood. Unlike donated blood, these “blood substitutes” do not require refrigeration and have a long shelf life. Their very high Henry’s law constants for \(\ce{O_2}\) result in dissolved oxygen concentrations comparable to those in normal blood.
The Henry’s law constant for \(\ce{O_2}\) in water at 25°C is \(1.27 \times 10^{-3} M/atm\), and the mole fraction of \(\ce{O_2}\) in the atmosphere is 0.21. Calculate the solubility of \(\ce{O_2}\) in water at 25°C at an atmospheric pressure of 1.00 atm.
Given: Henry’s law constant, mole fraction of \(\ce{O_2}\), and pressure
Asked for: solubility
Strategy:
- Use Dalton’s law of partial pressures to calculate the partial pressure of oxygen.
- Use Henry’s law (Equation \(\ref{11.61}\)) to calculate the solubility, expressed as the concentration of dissolved gas.
Solution:
A According to Dalton’s law, the partial pressure of \(O_2\) is proportional to the mole fraction of \(O_2\):
\[P_A = \chi_A P_t = (0.21)(1.00\; atm) = 0.21\; atm \nonumber\]
B From Henry’s law, the concentration of dissolved oxygen under these conditions is
\[[\ce{CO_2}]=k_H P_{O_2}=(1.27 \times 10^{-3}\; M/\cancel{atm}) (0.21\; \cancel{atm}) =2.7 \times 10^{-4}\; M \nonumber\]
To understand why soft drinks “fizz” and then go “flat” after being opened, calculate the concentration of dissolved \(CO_2\) in a soft drink:
- bottled under a pressure of 5.0 atm of \(CO_2\)
- in equilibrium with the normal partial pressure of \(CO_2\) in the atmosphere (approximately \(3 \times 10^{-4} \;atm\)). The Henry’s law constant for \(CO_2\) in water at 25°C is \(3.4 \times 10^{-2}\; M/atm\).
- Answer a
-
0.17 M
- Answer b
-
\(1 \times 10^{-5} M\)
Summary
The vapor pressure of the solution with volatile solute and solvent is proportional to the mole fraction of solute and solvent in the solution, via a modified version of Raoult’s law discussed previously. Solutions that obey Raoult’s law are called ideal solutions. Most real solutions exhibit positive or negative deviations from Raoult’s law. In an ideal solution, the interactions are there, but they are all energetically identical. Thus in an ideal solution of molecules A and B, A—A and B—B attractions are the same as A—B attractions. This is the case only when the two components are chemically and structurally very similar.
The solubility of most substances depends strongly on the temperature and, in the case of gases, on the pressure. The solubility of most solid or liquid solutes increases with increasing temperature. The components of a mixture can often be separated using fractional crystallization, which separates compounds according to their solubilities. The solubility of a gas decreases with increasing temperature. Henry’s law describes the relationship between the pressure and the solubility of a gas.

