Workgroup 3: Using Symmetry to Solve Integrals
- Page ID
- 54316
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Q1
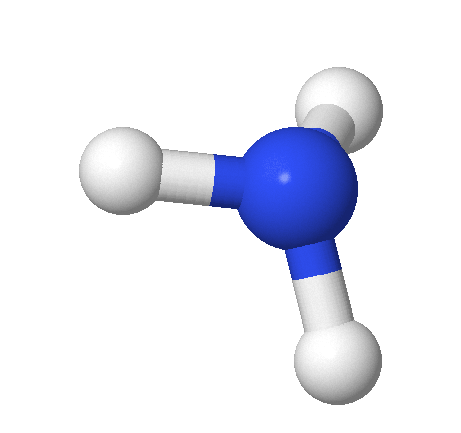
For ammonia: identify its point group with corresponding symmetries. How many different irreducible representations are in the point group for ammonia?
Q2
Without looking at the character table, how do you expect the \(p_{2x}\) atomic orbital on the central nitrogen atom to behave (i.e., symmetry or antisymmetric or none) to each of the symmetry elements of the molecule. Write the mathematical representation for this operation (i.e, in \(C_{2v}\) we would write \(\hat{C_2} p_{2z} = (+1) p_{2z}\) for a symmetric symmetry; do this for all operations). There is a special term for irreducible representation of this orbital; what is it and why is it call that?
Q3
Without looking at the character table, how do you expect the \(p_{2y}\) atomic orbital on the central nitrogen atom to behave (i.e., symmetry or antisymmetric or none) to each of the symmetry elements of the point group (write the mathematical equation for each operation). What is the irreducible representation of this orbital and how does it differ with the irreducible representation found for \(p_{2z}\) above?
Q4
The term SALC stands for a "Symmetry Adapted Linear Combination" and refers to different "predigested" mixing of atomic orbital typically on periphery of the molecules (like with ligands in inorganic molecules or hydogens in ammonia. It is similar to the "predigestion" of generating hybrid orbitals by mixing atomic orbitals together before making molecule orbitals (mathematically, it is the same as addressing all atomic orbitals directly). For ammonia, we can make several and they have the symmetries of the point group. Consider the totally symmetric SALC on each of the hydrogen atoms (labels A, B, C):
\[ | \psi _1 \rangle = N \left[ | 1s_A \rangle + | 1s_B \rangle + | 1s_C \rangle \right]\]
How does \( | \psi _1 \rangle \) behave to each of the symmetry operations of the relevant point group (describe it both in words and the relevant mathematical equation like above)? What is the irreducible representation of \( | \psi _1 \rangle \)?
Q5
For each of the symmetry operations outlined above for the \( | \psi _1 \rangle \) how do these integrals change:
- \( \langle \psi | \psi _1 \rangle \)
- \( \langle p_{2z} (N) | p_z (N) \rangle\)
- \( \langle p_{2y} (N) | p_{2y} (N) \rangle\)
Explain these trends in words.
Q6
The direct product of two irreducible representations is obtained by multiplying the respective characters of the representations. The result is again an irreducible representation of the same group. For example, in the \(C_{2V}\) point group the direct product of \(A_1\) and \(B_2\) (\(A_1 \otimes B_2\)):
| \(C_{2v}\) | \(E\) | \(C_2\) | \(\sigma_v\) | \(\sigma'_v\) |
|---|---|---|---|---|
| \(A_2\) | 1 | 1 | -1 | -1 |
| \(B_2\) | 1 | -1 | -1 | 1 |
| \(A_1 \otimes B_2\) | \(1 \times 1 =1\) | \(1 \times -1 = -1\) | \(-1 \times -1 = 1\) | \(-1 \times 1 =1\) |
From inspection of the irreducible representations of the \(C_{2v}\) point group, we can see that the irreducible representation for this piecewise multiplication procedure ("Direct Product) is
\[A_1 \otimes B_2 = B_1\]
Doing this for all possible multiplications for the \(C_{2v}\) point group results in a Direct Product Table:
| \(C_{2v}\) | \(A_1\) | \(A_2\) | \(B_1\) | \(B_2\) |
|---|---|---|---|---|
| \(A_1\) | ||||
| \(A_2\) | \(B_1\) | |||
| \(B_1\) | ||||
| \(B_2\) |
Complete the Direct Product table above for \(C_{2V}\) point group.
Q7
Construct the Direct Product table for the point group associated with ammonia.
Q8
It was argued in class that for a general integral to be non-zero, the integrand must contain (or be) the totally symmetric irreducible representation. This is basically saying that no symmetry operation on the integral (or specifically all the functions in the integrand) will result in a -1 character (i.e., antisymmetric or "odd"). Using the direct product table above evaluate the irreducible representation of the following functions for ammonia:
- \( | p_{2z} \rangle | p_{2y} \rangle \)
- \( | p_{2y} \rangle | p_{2z} \rangle \)
- \( | p_{2z} \rangle | \psi _1 \rangle \)
- \( | p_{2z} \rangle | \psi _2 \rangle \) (where \(| \psi _2 \rangle \) has \(E\) symmetry
Q9
Evaluate if the following integrals are zero or non-zero based on symmetry
- \( \langle p_{2z} | p_{2y} \rangle \)
- \( \langle p_{2y} | p_{2z} \rangle \)
- \( \langle p_{2z} | \psi _1 \rangle \)
- \( \langle p_{2z} | \psi _2 \rangle \) (where \(| \psi _2 \rangle \) has \(E\) symmetry
Q10
Using the direct product table above evaluate the irreducible representation of the following functions for ammonia where \(\hat{H}\) is the Hamiltonian and have the totally symmetry irrepresentation):
- \( \hat{H} | p_{2z} \rangle | p_{2y} \rangle \)
- \( \hat{H} | p_{2y} \rangle | p_{2z} \rangle \)
- \( \hat{H} | p_{2z} \rangle | \psi _1 \rangle \)
- \( \hat{H} | p_{2z} \rangle | \psi _2 \rangle \) (where \(| \psi _2 \rangle \) is a SALC with \(E\) symmetry
Q11
Using the direct product table above evaluate the irreducible representation of the following functions for ammonia where \(\hat{H}\) is the Hamiltonian and have the totally symmetry irrepresentation):
- \( \langle p_{2z} | \hat{H} | p_{2y} \rangle \)
- \( \langle p_{2y} | \hat{H} | p_{2z} \rangle \)
- \( \langle p_{2z} | \hat{H} |\psi _1 \rangle \)
- \( \langle p_{2z} | \hat{H} | \psi _2 \rangle \) (where \(| \psi _2 \rangle \) is a SALC with \(E\) symmetry
Q12
Using the direct product table above evaluate the irreducible representation of the following functions for ammonia where \(\hat{OH}\) is an operator with \(A_2\) symmetry):
- \( \hat{O} | p_{2z} \rangle | p_{2y} \rangle \)
- \( \hat{O} | p_{2y} \rangle | p_{2z} \rangle \)
- \( \hat{O} | p_{2z} \rangle | \psi _1 \rangle \)
- \( \hat{O} | p_{2z} \rangle | \psi _2 \rangle \) (where \(| \psi _2 \rangle \) is a SALC with \(E\) symmetry
Q13
Evaluate if the following integrals are zero or non-zero based on symmetry
- \( \langle p_{2z} | \hat{O} | p_{2y} \rangle \)
- \( \langle p_{2y} | \hat{O} | p_{2z} \rangle \)
- \( \langle p_{2z} | \hat{O} |\psi _1 \rangle \)
- \( \langle p_{2z} | \hat{O} | \psi _2 \rangle \) (where \(| \psi _2 \rangle \) is a SALC with \(E\) symmetry

