6.E: The Hydrogen Atom (Exercises)
- Page ID
- 92391
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Solutions to select questions can be found online.
6.5
\[\int_{-1}^{1} T_n(x)T_m(x) \frac{1}{\sqrt{1-x^2}}dx= \begin{cases} 0, & n \neq m \\ \pi, & n=m=0 \\ \pi/2, & n=m \neq 0 \end{cases} \nonumber\]
First 6 Chebyshev Polynomials
\[ \begin{align*} T_0(x) &=1 \\[4pt] T_1(x)&=x \\[4pt] T_2(x)&=2x^2-1 \\[4pt] T_3(x) &=4x^3-3x \\[4pt] T_4(x) &=8x^4-8x^2+1 \\[4pt] T_5(x) &=16x^5-20x^3+5x \end{align*}\]
Use the orthogonality of Chebyshev polynomials to determine what the following polynomials are equal to
- \(\int_{-1}^{1} x^2 \frac{dx}{\sqrt{1-x^2}} \)
- \(\int_{-1}^{1} 4x^3-2x \frac{dx}{\sqrt{1-x^2}} \)
- \(\int_{-1}^{1} 1 \frac{dx}{\sqrt{1-x^2}} \)
- \(\int_{-1}^{1} 4x^4-4x^2+1 \frac{dx}{\sqrt{1-x^2}} \)
- Solution
-
- x^2= T1*T1; therefore the answer is π /2
- here the following polynomial is not a product of either Chebyshev polynomials; therefore, answer is doesn't follow orthogonality conditions
- 1=T0*T0; therefore, answer is π
- x^4-4x^2+1= T2*T2; therefore the answer is π/2
6.6
Use Eq. 6.47 to generate the radial functions \(R_{nl}\left(r\right)\) for \(n=1,2\).
- Solution
-
\[R_{10}\left(r\right)={\left\{\dfrac{\left(1-0-1\right)!}{2\left(1\right){\left[\left(1+0\right)!\right]}^3}\right\}}^{\dfrac{1}{2}}{\left(\dfrac{2}{1a_0}\right)}^{\dfrac{0+3}{2}}r^0e^{-\dfrac{r}{1a_0}}L^1_1\left(\dfrac{2r}{1a_0}\right)\nonumber \]
\[R_{10}\left(r\right)=-{\left\{\dfrac{1}{2}\right\}}^{\dfrac{1}{2}}{\left(\dfrac{2}{a_0}\right)}^{\dfrac{3}{2}}e^{-\dfrac{r}{a_0}}\nonumber \]
\[R_{20}\left(r\right)={\left\{\dfrac{\left(2-0-1\right)!}{2\left(2\right){\left[\left(2+0\right)!\right]}^3}\right\}}^{\dfrac{1}{2}}{\left(\dfrac{2}{2a_0}\right)}^{\dfrac{0+3}{2}}r^0e^{-\dfrac{r}{2a_0}}L^1_2\left(\dfrac{2r}{2a_0}\right)\nonumber \]
\[R_{20}\left(r\right)={\left\{\dfrac{1}{32}\right\}}^{\dfrac{1}{2}}{\left(\dfrac{1}{a_0}\right)}^{\dfrac{3}{2}}e^{-\dfrac{r}{2a_0}}\left(-2!\left(2-\dfrac{r}{a_0}\right)\right)\nonumber \]
\[R_{20}\left(r\right)=-2{\left\{\dfrac{1}{32}\right\}}^{\dfrac{1}{2}}{\left(\dfrac{1}{a_0}\right)}^{\dfrac{3}{2}}e^{-\dfrac{r}{2a_0}}\left(\left(2-\dfrac{r}{a_0}\right)\right)\nonumber \]
\[R_{21}\left(r\right)={\left\{\dfrac{\left(2-1-1\right)!}{2\left(2\right){\left[\left(2+1\right)!\right]}^3}\right\}}^{\dfrac{1}{2}}{\left(\dfrac{2}{2a_0}\right)}^{\dfrac{1+3}{2}}r^1e^{-\dfrac{r}{2a_0}}L^3_3\left(\dfrac{2r}{2a_0}\right)\nonumber \]
\[R_{21}\left(r\right)=-6{\left\{\dfrac{1}{864}\right\}}^{\dfrac{1}{2}}{\left(\dfrac{1}{a_0}\right)}^2r^1e^{-\dfrac{r}{2a_0}}\nonumber \]
6.29
Compare \(\psi_{310}\) and \(\psi_{311}\).
Hint: What do the subscripts tell you about the wave function? What do they denote?
- Solution
-
The first subscript tells you the quantum number \(n\). The second denotes the angular momentum \(l\). The last denotes the magnetic spin number \(m_l\). These two functions have the same \(n\) values, and thus they are degenerate.
6.30
What is the probability density of the 3p orbital by evaluating
\[\left (\sum_{m=-1}^{1}\psi_{31m}^{2}\right )\nonumber \]
- Solution
-
\[ \begin{align*} \sum_{m=-1}^{1}\psi_{31m}^{2} &=\left (\dfrac{2}{6561\pi}\right )\left (\dfrac{z^{3}}{a_o^{3}}\right )\sigma^{3}\left (6-\sigma\right )^{2}\exp^{\dfrac{-2\sigma}{3}} \left (\cos^{2} \theta+\sin^{2} \theta \cos^{2} \phi + \sin^{2} \theta \sin^{2} \phi \right ) \\[4pt] \sum_{m=-1}^{1}\psi_{31m}^{2} &=\left (\dfrac{2z^{3}\sigma^{2} \left (6-\sigma\right )^{2}\exp^{\dfrac{-2\sigma}{3}}}{6561\pi a_o^{3}}\right ) \left (\cos^{2}\theta+\sin^{2}\theta \left(\cos^{2}\phi+\sin^{2}\phi \right ) \right)\\[4pt] \sum_{m=-1}^{1}\psi_{31m}^{2} &=\left (\dfrac{2z^{3}\sigma^{2}\left (6-\sigma\right )^{2}\exp^{\dfrac{-2\sigma}{3}}}{6561\pi a_o^{3}}\right )\end{align*}\]
6.34
Find the energy, and wavefunction for a single electron located in the 2p orbital of the hydrogen atom. Include all possible wavefunctions.
- Solution
-
Identify the quantum numbers for the electron of interest (in our case, \(n=2\); \(l =1\)). Energy of the electron can be defined as
\[E_n = \dfrac{-m_ee^4}{8n^2\epsilon_o^2h^2} \nonumber \]
this leads us to
\[E_2 = \dfrac{-m_ee^4}{32\epsilon_o^2h^2} \nonumber \]
we have two possible wave functions
\[ \Psi_{210}= \dfrac{1}{\sqrt{32}} (\dfrac{z}{a_o})^{3/2}\sigma/e^{-\sigma/2} \cos{\theta} \nonumber \]
and
\[ \Psi_{21\pm1}= \dfrac{1}{\sqrt{32}} (\dfrac{z}{a_o})^{3/2}\sigma/e^{-\sigma/2} \sin{\theta}e^{\pm i\theta } \nonumber \]
6.37
The Hamiltonian is given by \(\hat{H} = \dfrac{-\hbar}{2m}\nabla^2 + V\) is an Hermitian Operator. Using this fact, show that
\[\int{\psi^*[\hat{H},\hat{A}]\psi} d\tau = 0\nonumber \]
where \(\hat{A}\) is any operator.
- Solution
-
Through the commutation relation
\[\int{\psi^*\hat{H}\hat{A}\psi} d\tau - \int{\psi^*\hat{A}\hat{H}\psi} d\tau= 0\nonumber \]
because \(\hat{H}\) is a Hermitian operator, the above goes to
\[\int{(\psi\hat{H})^*\hat{A}\psi} d\tau - \int{\psi^*\hat{A}(\hat{H}\psi)} d\tau= 0\nonumber \]
\[E\int{\psi^*\hat{A}\psi} d\tau - E\int{\psi^*\hat{A}\psi} d\tau= 0\nonumber \]
6.38
Prove that \(\langle{\hat{K}}\rangle \ = \ \langle{V}\rangle = E/2\) for a harmonic oscillator using the virial theorem
- Solution
-
The virial theorem gives us,
\[\Bigg\langle{x\dfrac{\partial V}{\partial x} + y\dfrac{\partial V}{\partial y} + z\dfrac{\partial V}{\partial z}}\Bigg\rangle = 2\langle{\hat{K}}\rangle\nonumber \]
For a three-dimensional harmonic oscillator,
\[V(x,y,z) = \dfrac{k_xx^2}{2} + \dfrac{k_yy^2}{2} + \dfrac{k_zz^2}{2}\nonumber \]
Therefore,
\[x\dfrac{\partial V}{\partial x} + y\dfrac{\partial V}{\partial y} + z\dfrac{\partial V}{\partial z} = k_xx^2 + k_yy^2 + k_zz^2 = 2V\nonumber \]
and substituting into the equation given by the virial theorem gives us \(2\langle{V}\rangle = 2\langle{\hat{K}}\rangle\). Because \(\langle{\hat{K}}\rangle + \langle{V}\rangle = E\), we can also write
\[\langle{\hat{K}}\rangle = \langle{V}\rangle = \dfrac{1}{2}E\nonumber \]
6.41
Find the expected values of \(1/r\) and \(1/r^2\) for a hydrogenlike atom in the \(2p_z\) orbital.
- Solution
-
The \(2p_z\) orbital:
\[Ψ_{210} = \dfrac{1}{4\sqrt{2π}} (Z/a_0)^{3/2}\rho e^{-\rho} \sinθ \cos ϕ \,dθ \nonumber \]
where \(\rho=Zr/a_o\)
\[\langle 1/r \rangle _{Ψ210}= \int_{0}^2π \, dθ \int\limits_{0}^{π}\, \sin θ \cos 2ϕ dθ \int\limits_{0}^{∞}\ (Z^{3/2}/a_o^{3/2}4\sqrt{2π}^{2*}r^2p^*e^{-p*}(1/r) dr\nonumber \]
\[\int_0^{2π}\, dθ = 2π\nonumber \]
\[\int_0^π \, \sinθ \cos^2 \,ϕ \,dθ = \dfrac{2}{3}\nonumber \]
\[\int _ 0^∞ \ (Z^{3/2}/a_o^{3/2}4\sqrt{2π})^2 r^2 \phi e-{\rho}(1/r)dr =(Z^3/a_o^332π)^* [3!/(Z/ao)^4]\nonumber \]
\[ \langle 1/r \rangle_{Ψ210} = (Z^3/a_o^332π)(2π)(2/3)[3!/(Z/ao)^4]\nonumber \]
Simplify to get:
\[\left \langle \dfrac{1}{r} \right \rangle _{Ψ_{210}} = \dfrac{Z}{4a_o}\nonumber \]
For the hydrogen atom \(Z=1\), therefore
\[\langle \dfrac{1}{r} \rangle _{Ψ_{210}} = \dfrac{1}{4a_o}\nonumber \]
For \(\langle \dfrac{1}{r^2} \rangle \)
\[\langle \dfrac{1}{r^2} \rangle_{Ψ_{210}} = \int_{0}^2π \, dθ \int\limits_{0}^{π}\, \sin θ \cos^2\, ϕ\,dθ \int\limits_{0}^{∞}\ (Z^3/2/a_o^3/24\sqrt{2π})^2r^2pe^{-p}(1/r^2)dr\nonumber \]
\[\int\limits_{0}^{2π}\, dθ = 2π\nonumber \]
\[\int\limits_{0}^{π}\, \sinθ \cos^2ϕdθ = 2/3\nonumber \]
\[\int \limits_{0}^{∞}\ (Z^{3/2}/a_o^{3/2}4\sqrt{2π})^2r2pe^{-p}(1/r^2)dr = (Z^3/a_o^332π) [2!/(Z/ao)^3]\nonumber \]
\[\langle 1/r^2 \rangle Ψ_{210} =(Z^3/a_o^332π)(2π)(2/3)[2!/(Z/a_o)^3]\nonumber \]
Simplify to get:
\[\langle \dfrac{1}{r^2} \rangle _{Ψ_{210}} =\dfrac{Z^2}{12a_o^2} \nonumber \]
where \(Z=1\)
\[\langle \dfrac{1}{r^2} \rangle _{Ψ_{210}} = \dfrac{1}{12a_o^2} \nonumber \]
6.43
Derive the classical magnetic moment of an electron orbiting a nucleus in terms of charge, mass and angular momentum.
- Solution
-
We can begin by recalling the classical expression for a magnetic moment,
\[\mu = IArea\nonumber \]
Where \(I\) is the current the electron makes by revolving around the nucleus. The definition of current is
\[I = \dfrac{Q}{time}\nonumber \]
In this case \(Q\) is simply the charge \((q_e)\) of the electron and \(time\) is the time it takes the electron to orbit the nucleus once. The area is the of loop that the electron takes when revolving around the nucleus. We also know from classical mechanics that \(x=vt\). solving for \(t\) and evaluating \(x\) to be \(2\pi r\) for a circle. We can figure out the time of revolution to be,
\[t = \dfrac{x}{v}= \dfrac{2\pi r}{v}\nonumber \]
Our current equations becomes,
\[I = \dfrac{q_ev}{2\pi r}\nonumber \]
To introduce angular momentum \(L=m_evr\) we can multiply the right side of our current equation by \(\dfrac{m_er}{m_er}\) to arrive at
\[I = \dfrac{q_em_evr}{2\pi m_er^2} \\ I = \dfrac{q_eL}{2\pi m_er^2}\nonumber \]
Substituting in the area of a circle \((\pi r^2)\) we can show that,
\[\boxed{\mu = IArea = \dfrac{q_eL}{2m_e}}\nonumber \]
6.46
Find the magnitude of the splitting shown in figure below. The magnetic field in the figure is at 20 T.
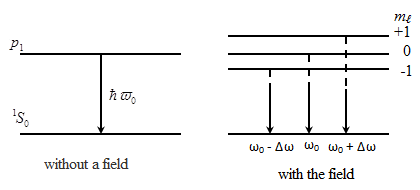
- Solution
-
We know from a previous problem that
\[\Delta E = E_{2} - E_{1} = \beta _{e}B_{z}(m_2 - m_1)\nonumber \]
In the 1\s\ state where m = 0 and in the 2\p\ state where m = 0, \pm\ 1. The condition will cause (m_{2} - m_{1}) become equal to 0, or \pm\ 1 which will affect the magnitude of splitting, calculated below
\[\Delta E = (9.274 * 10^{-24} J*T^{-1}) (20T)(1) \nonumber \]
\(\Delta E = 1.8548 * 10^{-22} J*T^{-1}\) or 0
6.47
Consider the transition between the \(l=1\) and the \(l=2\) states for atomic hydrogen. Determine the total number of possible allowed transitions between these two states in an external magnetic field given the following selection rules
- Light whose electric field vector is parallel to the external magnetic field's direction has a selection rule of \(\Delta m=0\) for allowed transitions.
- Light whose electric field vector is perpendicular to the external magnetic field's direction has a selection rule of \(\Delta m=\pm 1\) for allowed transitions.
- Solution
-
An external magnetic field splits a state with given values n and \(l\) into \(2l+1\) levels. So the \(l=1\) state will be split into three states (\(m=0, \pm 1\)) and the \(l=2\) state will be split into five states (\(m=0, \pm 1, \pm 2\)). This means that the \(l=1 \rightarrow l=2\) transition will have a possible of 15 transitions (ignoring any selection rules that reduce this number).
Using the selection rule \(\Delta m=0\), then three transitions are possible: \(m=0\), \(m=1\), \(m=-1\) Using the selection rule \(\Delta m= \pm 1\), then six transitions are possible:\(l=1\) \(\rightarrow\) \(l=2\) Relative Orientation of light Polarization to Magnetic field m=0 m=1 parallel m=0 m=-1 parallel m=1 m=2 perpendicular m=1 m=0 perpendicular m=-1 m=-2 perpendicular m=-1 m=0 perpendicular
6.49
Prove that
\[\hat{L_+}\hat{L_-} - \hat{L_-}\hat{L_+} = 2\hbar\hat{L_z}\nonumber\]
given that
\[\hat{L_+} = \hat{L_x} + i\hat{L_y}\nonumber\]
and
\[\hat{L_-} = \hat{L_x} - i\hat{L_y}.\nonumber\]
- Solution
-
\[\hat{L_+}\hat{L_-} = (\hat{L_x} + i\hat{L_y})(\hat{L_x} - i\hat{L_y}) = \hat{L^2_x} + \hat{L^2_y} - i\hat{L^2_x}\hat{L^2_y} + i\hat{L^2_y} \hat{L^2_x} = \hat{L^2_x} + \hat{L^2_y} +i[\hat{L_y},\hat{L_x}]\nonumber\]
\[\hat{L_+}\hat{L_-} = \hat{L^2} - \hat{L^2_z} +\hbar \hat{L_z}\nonumber\]
and
\[\hat{L_-}\hat{L_+} = (\hat{L_x} - i\hat{L_y})(\hat{L_x} + i\hat{L_y}) = \hat{L^2_x} + \hat{L^2_y} +i\hat{L^2_x}\hat{L^2_y} - i\hat{L^2_y} \hat{L^2_x} = \hat{L^2_x} + \hat{L^2_y} +i[\hat{L_x},\hat{L_y}]\nonumber\]
\[\hat{L_-}\hat{L_+} = \hat{L^2} - \hat{L^2_z} - \hbar \hat{L_z}\nonumber\]
thus
\[\hat{L_+}\hat{L_-} - hat{L_-}\hat{L_+} = \hat{L^2} - \hat{L^2_z} +\hbar \hat{L_z} - \hat{L^2} + \hat{L^2_z} - \hbar \hat{L_z}\nonumber\]
\[\hat{L_+}\hat{L_-} - \hat{L_-}\hat{L_+} = 2\hbar \hat{L_z}\nonumber\]
6.49
Show that the commutative property applies to \[\hat{L}_{-}\hat{L}_{+}\nonumber \]
- Solution
-
\[\hat{L}_{-}\hat{L}_{+} = \hat{L}_{+}\hat{L}_{-}\nonumber \]
\[\hat{L}_{-} = \hat{L}_{x} - i \hat{L}_{y}\nonumber \]
and
\[\hat{L}_{+} = \hat{L}_{x} + i \hat{L}_{y}\nonumber \]
so
\[\hat{L}_{-}\hat{L}_{+}=[\hat{L}_x -i\hat{L}_y][\hat{L}_x + i \hat{L}_y]\nonumber \]
\[= \hat{L}_{x}^2 + i \hat{L}_{x} \hat{L}_{y} - i \hat{L}_{x}\hat{L}_{y} + \hat{L}_{y}^2\nonumber \]
and
\[\hat{L}_{+}\hat{L}_{-}= [\hat{L}_{x} + i\hat{L}_{y}][\hat{L}_{x}-i\hat{L}_{y}]\nonumber \]
\[= \hat{L}_{x}^2 -i \hat{L}_{y}\hat{L}_{x}+ i\hat{L}_{x}\hat{L}_{y}+ \hat{L}_{y}^2\nonumber \]
which shows that
\[\hat{L}_{-}\hat{L}_{+}= \hat{L}_{+}\hat{L}_{-}\nonumber \]
Q7.29
Calculate the ground-state energy for particle in the box model using variational method.
- Solution
-
Variational method equations is:
\[E_\phi=\dfrac{\langle\phi | \hat{H}| \phi\rangle}{\langle \phi | \phi \rangle}\nonumber \]
where the wavefunctions are unnormalized
The unnormalized Schrödinger equation for PIB:
\[\phi(x)=A \sin (\dfrac{xn\pi}{L})\nonumber \]
\[\langle\phi | \phi\rangle\nonumber \] \[= A = \sqrt[]{\dfrac{2}{L}}\nonumber \]
and
\[\langle \phi | \hat{H}| \phi\rangle\nonumber \] \[= \dfrac{n^2 h^2}{8mL^2}\cdot \sqrt[]{\dfrac{2}{L}}\nonumber \] so
\[E_\phi = \dfrac{\dfrac{n^2 h^2}{8mL^2}\cdot \sqrt[]{\dfrac{2}{L}}}{\sqrt[]{\dfrac{2}{L}}}\nonumber \]
so
\[E_\phi = \dfrac{n^2h^2}{8mL^2}\nonumber \]
where n=1 we get
\[E_\phi = \dfrac{h^2}{8mL^2}\nonumber \]
6.50
If two functions commute, they have mutual eigenfunctions, such as \(\hat{L}\)2 and \(\hat{L}\)\(z\). These mutual eigenfunctions are also known as spherical harmonics, \(Y\)\(l\)\(m\)(\(\theta\), \(\phi\)), however this information is not pertinent in this case. Let
\(\psi\)\(\alpha\)\(\beta\) be a mutual eigenfunction of \(\hat{L}\)2 and \(\hat{L}\)\(z\) so that
\(\hat{L}\)\(z\) \(\psi\)\(\alpha\)\(\beta\) = \(\beta\)2\\(\alpha\)\(\beta\)
and
\(\hat{L}\)\(z\) \(\psi\)\(\alpha\)\(\beta\) = \(\alpha\)\(\psi\)\(\alpha\)\(\beta\)
Now let
\(\psi\)\(\alpha\)\(\beta\)+1 = \(\hat{L}\)+\(\psi\)\(\alpha\)\(\beta\)
Show that
\(\hat{L}\)\(z\)\(\psi\)\(\alpha\)\(\beta\)+1 = (\(\alpha\) + \(\hbar\))\(\psi\)\(\alpha\)\(\beta\)+1
and
\(\hat{L}\)2\(\psi\)\(\alpha\)\(\beta\)+1 = \(\beta\)2\(\psi\)\(\alpha\)\(\beta\)+1
This proves that if \(\alpha\) is an eigenvalue of \(\hat{L}\)\(z\), then \(\alpha\) + \(\hbar\) also is an eigenvalue.
- Solution
-
Solve this problem as given below:
\(\psi\)\(\alpha\)\(\beta\)+1 = \(\hat{L}\)+\(\psi\)\(\alpha\)\(\beta\)
\(\hat{L}\)\(z\) \(\psi\)\(\alpha\)\(\beta\)+1 =\(\hat{L}\)\(z\) \(\hat{L}\)+\(\psi\)\(\alpha\)\(\beta\)
= (\(\hat{L}\)\(z\) \(\hat{L}\)\(x\) + \(i\)\(\hat{L}\)\(z\) \(\hat{L}\)\(y\) )\(\psi\)\(\alpha\)\(\beta\)
\(z\), \(\hat{L}\)\(x\)] + \(\hat{L}\)\(x\) \(\hat{L}\)\(z\) + \(i\)[\(\hat{L}\)\(z\), \(\hat{L}\)\(y\)] + \(i\)\(\hat{L}\)\(y\) \(\hat{L}\)\(z\))\(\psi\)\(\alpha\)\(\beta\)
\(y\) + \(\hat{L}\)\(z\)\(\hat{L}\)\(x\) + \(i\)\(\hbar\)\(\hat{L}\)\(x\) + \(\hat{L}\)\(y\)\(\hat{L}\)\(z\)) \(\psi\)\(\alpha\)\(\beta\)
\(\hat{L}\)\(+\)\(\hat{L}\)\(z\) + \(\hbar\)\(\hat{L}\)\(+\))\(\psi\)\(\alpha\)\(\beta\)
\(+\)(\(\alpha\) + \(\hbar\))\(\psi\)\(\alpha\)\(\beta\)
\(\alpha\)\(\beta\)+1
Therefore proven.
Finally, you can write:
\(\hat{L}\)2\(\psi\)\(\alpha\)\(\beta\)+1 = \(\hat{L}\)2\(\hat{L}\)\(+\)\(\psi\)\(\alpha\)\(\beta\)
= (\(\hat{L}\)2\(\hat{L}\)\(x\) + \(i\)\(\hat{L}\)2\(\hat{L}\)\(y\))\(\psi\)\(\alpha\)\(\beta\)
=([\(\hat{L}\)2,\(\hat{L}\)\(x\)] + \(\hat{L}\)\(x\)\(\hat{L}\)2 + \(i\)[\(\hat{L}\)2,\(\hat{L}\)\(y\)] + \(i\)\(\hat{L}\)\(y\)\(\hat{L}\)2)\(\psi\)\(\alpha\)\(\beta\)
\(x\)\(\hat{L}\)2 + \(i\)\(\hat{L}\)\(y\)\(\hat{L}\)2)\(\psi\)\(\alpha\)\(\beta\)
\(+\)\(\beta\)2\(\psi\)\(\alpha\)\(\beta\)
2\(\psi\)\(\alpha\)\(\beta\) +1
Therefore proven.

