19: More on Hydrogen Wavefunction, Electronic Spectroscopy and Effective Charge
- Page ID
- 40098
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Last Lecture addressed the angular moment of an electron revolving around the nucleus. This is described by the \(l\) quantum number and an electron in any non-spherical orbital (i.e., an s orbital) will have an angular moment (you should know formula). The \(m_{\ell}\) quantum number designates the orientation of that angular moment wrt the z-axis (and there is a formula for that too) and the degeneracy can be partial broken by magnetic fields. We discussed that we cannot always do a one-to-one correspondence between quantum numbers to orbitals. We discussed basic spectroscopy of H-like system and specifically selection rules (for n,l, and ml). We introduced the He system, discussed we cannot solve it and need to do approximations. We discussed the first approximation, which is the worst possible one.
The \(m_{\ell}\) Quantum Number and Magnetic Fields
The magnetic quantum number, designated by the letter \(m_{\ell}\), is the third quantum numbers which describe the unique quantum state of an electron. The magnetic quantum number distinguishes the orbitals available within a subshell, and is used to calculate the azimuthal component of the orientation of the orbital in space. As with our discussion of rigid rotors, the quantum number \(m_{\ell}\) refers to the projection of the angular momentum in this arbitrarily chosen direction, conventionally called the \(z\) direction or quantization axis. \(L_z\), the magnitude of the angular momentum in the z direction, is given by the formula
\[ L_z = m_{\ell} \hbar \label{eq1}\]
The quantum number \(m_{\ell}\) refers, loosely, to the direction of the angular momentum vector. The magnetic quantum number \(m_{\ell}\) only affects the electron's energy if it is in a magnetic field because in the absence of one, all spherical harmonics corresponding to the different arbitrary values of \(m_{\ell}\) are equivalent.
Zeeman Effect
Magnetism results from the circular motion of charged particles. This property is demonstrated on a macroscopic scale by making an electromagnet from a coil of wire and a battery. Electrons moving through the coil produce a magnetic field, which can be thought of as originating from a magnetic dipole or a bar magnet.
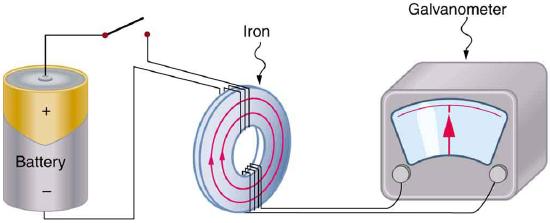
Electrons in atoms also are moving charges with angular momentum so they too produce a magnetic dipole, which is why some materials are magnetic. A magnetic dipole interacts with an applied magnetic field, and the energy of this interaction is given by the scalar product of the magnetic dipole moment (magnetic moment (\(\vec{\mu _m}\) ) and the magnetic field, \(\vec{B}\).
\[E_B = - \vec{\mu} _m \cdot \vec{B} \label {8.4.1}\]
Magnets are acted on by forces and torques when placed within an external applied magnetic field (Figure \(\PageIndex{2}\)). In a uniform external field, a magnet experiences no net force, but a net torque. The torque tries to align the magnetic moment (\(\vec{\mu} _m\)) of the magnet with the external field \(\vec{B}\). The magnetic moment of a magnet points from its south pole to its north pole.
The magnetic quantum number determines the energy shift of an atomic orbital due to an external magnetic field (this is called the Zeeman effect) — hence the name magnetic quantum number. However, the actual magnetic dipole moment of an electron in an atomic orbital arrives not only from the electron angular momentum, but also from the electron spin, expressed in the spin quantum number, which is the fourth quantum number. \(m_s\) and discussed in the next chapter.
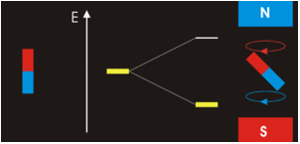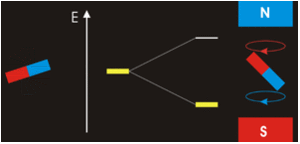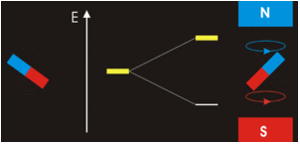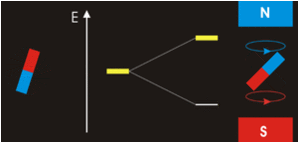
Electrons with non-zero angular momenta exhibit magnetic moments, which depend on the specific wavefunctions the electrons occupy (and specifically the \(\ell\) quantum number). In the absence of an external magnetic field, different orientations of this magnetic field (i.e., electrons in wavefunctions with different \(m_{\ell}) values) will have the same energy. In the presence of an external field, the degeneracy of these different wavefunctions break. Assume the external magnetic field is oriented in the z-direction, predict the splitting patterns for an electron in the following orbitals:
- 1s orbital
- 2p orbitals (consider each orbital)
- 2s orbital
- 3d orbitals (consider each orbital)
- How do you think the splitting would be for a helium atom?
Which \(m_{\ell}\) number corresponds to which \(p\)-orbital?
The answer is complicated; while \(m_{\ell}=0\) corresponds to the \(p_z\), the orbitals for \(m_{\ell}=+1\) and \(m_{\ell}=−1\) lie in the xy-plane (see Spherical Harmonics), but not on the axes. The reason for this outcome is that the wavefunctions are usually formulated in spherical coordinates to make the math easier, but graphs in the Cartesian coordinates make more intuitive sense for humans. The \(p_x\) and \(p_y\) orbitals are constructed via a linear combination approach from radial and angular wavefunctions and converted into \(xy\) (this was discussed previously). Thus, it is not possible to directly correlate the values of \(m_{\ell}=±1\) with specific orbitals.
The notion that we can directly correlate the values of \(m_{\ell}=±1\) with specific orbitals is sometimes presented in introductory courses (not the Libretexts) to make a complex mathematical model just a little bit simpler and more intuitive, but it is incorrect.
The three wavefunctions for \(n=2\) and \(\ell=1\) are as follows (the spherical harmonics).
\[ \begin{align*} |Ψ_{2,1,0} \rangle &=r \cos θR(r) \\[4pt] |Ψ_{2,1,+1} \rangle &=−\dfrac{r}{2} \sinθ e^{iϕ} R(r) \\[4pt] |Ψ_{2,1,-1} \rangle &=+\dfrac{r}{2} \sinθ e^{-iϕ} R(r) \end{align*}\]
The notation is \(|Ψ_{n,l,m_{\ell}} \rangle\) with \(R(r)\) is the radial component of this wavefuction, \(θ\) is the angle with respect to the z-axis and \(ϕ\) is the angle with respect to the \(xz\)-plane.
\[R(r)=\sqrt{\dfrac{Z^5}{32\pi a_0^5}}\mathrm{e}^{-Zr/2a_0}\]
in which \(Z\) is the atomic number (or probably better nuclear charge) and \(a_0\) is the Bohr radius.
In switching from spherical to Cartesian coordinates, we make the substitution \(z=r \cos θ\), so:
\[|Ψ_{2,1,0} \rangle =z R(r)\]
This is \(Ψ_{2p_z}\) since the value of \(Ψ\) is dependent on \(z\): when \(z=0\); \(Ψ=0\), which is expected since \(z=0\) describes the \(xy\)-plane.
The other two wavefunctions are degenerate in the \(xy\)-plane. An equivalent statement is that these two orbitals do not lie on the x- and y-axes, but rather bisect them. Thus it is typical to take linear combinations of them to make the equations real and easier to conceptualize. We can do this because of the linearity of the Schrödinger equation.
If any set of wavefunctions is a solution to the Schrödinger equation, then any set of linear combinations of these wavefunctions must also be a solution.
In the equations below, we're going to make use of some trigonometry, notably Euler's formula:
\[\mathrm{e}^{\mathrm{i}\phi}=\cos{\phi}+\mathrm{i}\sin{\phi}\]
\[\sin{\phi} = \frac{\mathrm{e}^{\mathrm{i}\phi}-\mathrm{e}^{-\mathrm{i}\phi}}{2\mathrm{i}}\]
\[\cos{\phi} = \frac{\mathrm{e}^{\mathrm{i}\phi}+\mathrm{e}^{-\mathrm{i}\phi}}{2}\]
We're also going to use \(x=\sin θ\cos ϕ\) and \(y=\sin θ \sinϕ \).
\begin{align} \psi_{2p_x}=\frac{1}{\sqrt{2}}\left(\psi_{2,1,+1}-\psi_{2,1,-1}\right)=\frac{1}{2}\left(\mathrm{e}^{\mathrm{i}\phi}+\mathrm{e}^{-\mathrm{i}\phi} \right)r\sin{\theta}f(r)=r\sin{\theta}\cos{\phi}f(r)=xf(r) \\ \psi_{2p_y}=\frac{\mathrm{i}}{\sqrt{2}}\left(\psi_{2,1,+1}+\psi_{2,1,-1}\right)=\frac{1}{2\mathrm{i}}\left(\mathrm{e}^{\mathrm{i}\phi}-\mathrm{e}^{-\mathrm{i}\phi} \right)r\sin{\theta}f(r)=r\sin{\theta}\sin{\phi}f(r)=yf(r)\\ \end{align}
So, while \(m_{\ell}=0\) corresponds to \(|p_z \rangle\), \(m_{\ell}=+1\) and \(m_{\ell}=−1\) cannot be directly assigned to \(|p_x \rangle\) and \(|p_y \rangle\).
Rather \(m_{\ell}=\pm 1\) corresponds to {\(p_x \rangle\), \(p_y \rangle\)}. An alternative discription is that \(m_{\ell}=+1\) might correspond to \((|p_x \rangle\ + |p_y \rangle )\) and \(m_{\ell}=−1\) might correspond to \((|p_x \rangle\ - |p_y \rangle)\).
The Math is the same for Solving any Hydrogen-like (One electron) ion
The Hamiltonian for a one electron atom is given by is given by
\[\hat{H}_{electron} = -\dfrac {\hbar^2}{2\mu} \bigtriangledown^2 - \dfrac {Ze^2}{4\pi \epsilon_0 r}\label{7}\]
This only differs by the \(Z^2\) component from the hydrogen atom.
Solving \(\hat{H}\psi_n = E_n \psi_n\) gives \(E=-RZ^2/n^2\).
For example with He+, the 2s orbital
\(E_{He_{2s}}\) has \(z=2, n=2\), thus \(E_{He_{2s}} = -R\)
Spectroscopy of Hydrogen atoms
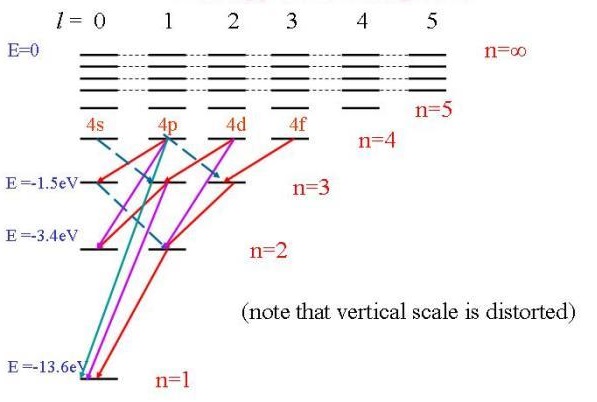
The solution of the Schrödinger equation for the hydrogen atom predicts that energy levels with \(n > 1\) can have several orbitals with the same energy. In fact, as the energy and n increase, the degeneracy of the orbital energy level increases as well. The number of orbitals with a particular energy and value for \(n\) is given by \(n_2\). Thus, each orbital energy level is predicted to be \(n_2\)-degenerate. This high degree of orbital degeneracy is predicted only for one-electron systems. For multi-electron atoms, the electron-electron repulsion removes the \(l\) degeneracy so only orbitals with the same \(m_{\ell}\) quantum numbers are degenerate.
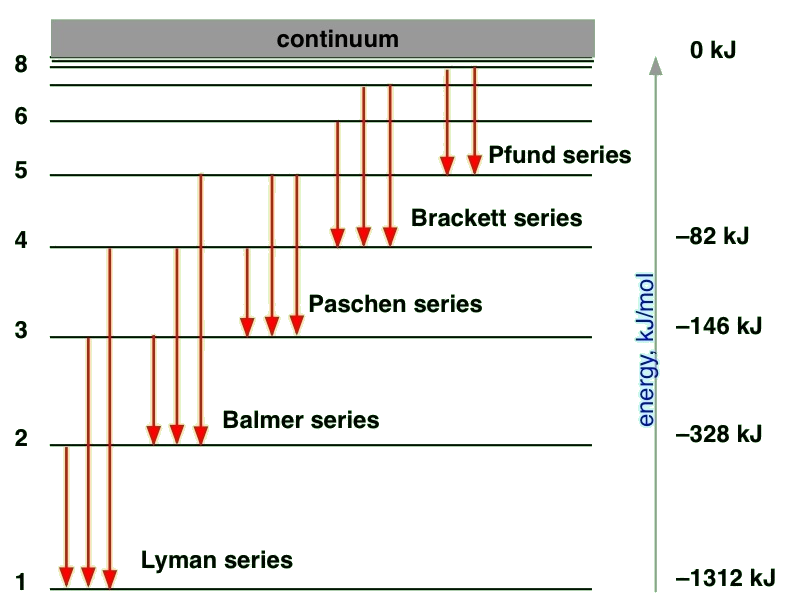
To understand the hydrogen atom spectrum, we also need to determine which transitions are allowed and which transitions are forbidden. This issue is addressed next by using selection rules that are obtained from the transition moment integral. Previously, we determined selection rules for the particle in a box, the harmonic oscillator, and the rigid rotor. Now we will apply those same principles to the hydrogen atom case by starting with the transition moment integral.
Transition requires a transfer from one state with its quantum numbers \((n_i, l_i, m_i)\) to another state \((n_f, l_f, m_f)\). The transition moment integral for a transition between an initial (\(i\)) state and a final (\(f\)) state of a hydrogen atom is given by
\[ \left \langle \mu _T \right \rangle = \int \psi ^* _{n_f, l_f, m_{l_f}} (r, \theta , \psi ) \hat {\mu} \psi _{n_i, l_i, m_{l_i}} (r, \theta , \psi ) d \tau \label {8.3.2a}\]
or in bra ket notation
\[ \left \langle \mu _T \right \rangle = \langle \psi ^*_{n_f, l_f, m_{l_f}} | \hat {\mu} | \psi _{n_i, l_i, m_{l_i}} \rangle \label{8.3.2b}\]
where the dipole moment operator is given by
\[ \hat {\mu} = - e \hat {r} \label{8.3.3}\]
The dipole moment operator expressed in spherical coordinates is
\[ \hat {\mu} = -er (\bar {x} \sin \theta \cos \psi + \bar {y} \sin \theta \sin \psi + \bar {z} \cos \theta \label {8.3.4}\]
The right hand side of Equation \ref{8.3.4} shows that there are three components of \(\left \langle \mu _T \right \rangle\) to evaluate in \ref{8.3.2}, where each component consists of three integrals: an \(r\) integral, a \(\theta \) integral, and a \(\psi \) integral.
Evaluation reveals that the \(r\) integral always differs from zero so
\[ \color{red} \Delta n = n_f - n_i = \text {not restricted} \label {8.3.5}\]
There is no restriction on the change in the principal quantum number during a spectroscopic transition; \(\Delta n\) can be anything. For absorption, \(\Delta n > 0 \), for emission \(\Delta n < 0\), and \(\Delta n = 0 \) when the orbital degeneracy is removed by an external field or some other interaction.
The selection rules for \(\Delta l \) and \(\Delta m_{\ell}\) come from the transition moment integrals involving \(\theta \) and \(\varphi\) in Equation \ref{8.3.3}. These integrals are the same ones that were evaluated for the rotational selection rules, and the resulting selection rules are
\[ \color{red} \Delta l = \pm 1\]
and
\[ \color{red} \Delta m_{\ell} = 0, \pm 1\]
These rules demand conservation of angular momentum. Since a photon carries an intrinsic angular momentum of 1.