22: Perturbation Theory
- Page ID
- 40109
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lectures 20 and 21 reviewed the basic steps in variational method, the linear variational method and the linear variation method with functions that have parameters that can float (e.g., a linear combination of Gaussians with variable widths in ab initio chemistry calculations). The latter two will be more applicable in the discussions of molecules using atomic orbitals as the basis set (the LCAO approximation). The final approximation, perturbation theory is introduced, but not used in an example.
Perturbation Theory
Perturbation theory is best for small changes to a known system and Hamiltonian is modified. The unperturbed Hamiltonian of a known system is modified by adding a perturbation. The perturbation can affect the potential, the kinetic energy part of the Hamiltonian, or both.
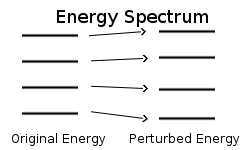
We begin with a Hamiltonian \(H^0\) having known eigenkets and eigenenergies:
\[ H^o | n^o \rangle = E_n^o | n^o \rangle \label{7.4.1}\]
The task is to find how these eigenstates and eigenenergies change if a small term \(H^1\) (e.g., an external field) is added to the Hamiltonian, so:
\[ ( H^0 + H^1 ) | n \rangle = E_n | n \rangle \label{7.4.2}\]
That is to say, on switching on \(H^1\) changes the wavefunctions
\[ \underbrace{ | n^o \rangle }_{\text{unperturbed}} \rightarrow \underbrace{|n \rangle }_{\text{Perturbed}}\label{7.4.3}\]
and energies
\[ \underbrace{ E_n^o }_{\text{unperturbed}} \rightarrow \underbrace{E_n }_{\text{Perturbed}} \label{7.4.4}\]
The basic assumption in perturbation theory is that \(H^1\) is sufficiently small that the leading corrections are the same order of magnitude as \(H^1\) itself, and the true energies can be better and better approximated by a successive series of corrections, each of order \(H^1/H^o\) compared with the previous one.
The strategy is to expand the true wavefunction and corresponding eigenenergy as series in \(H^1/H^o\). These series are then fed into Equation \(\ref{7.4.2}\), and terms of the same order of magnitude in \(H^1/H^o\) on the two sides are set equal. The equations thus generated are solved one by one to give progressively more accurate results.
To make it easier to identify terms of the same order in \(H^1/H^o\) on the two sides of the equation, it is convenient to introduce a dimensionless parameter \(\lambda\) which always goes with \(H^1\), and then expand both eigenstates and eigenenergies as power series in \(\lambda\),
\[ \color{red} | n \rangle = \sum _ i^m \lambda ^i| n^i \rangle \label{7.4.5}\]
\[ \color{red} E_n = \sum_{i=0}^m \lambda ^i E_n^i \label{7.4.6}\]
where \(m\) is how many terms in the expansion we are considering. The ket \(|n^i \rangle\) is multiplied by \(\lambda^i\) and is therefore of order \((H^1/H^o)^i\). For example, in first order perturbation theory, Equations \(\ref{7.4.5}\) are truncated at \(m=1\) (and setting \(\lambda=1\)):
\[ | n \rangle \approx | n^o \rangle + | n^1 \rangle \label{7.4.7}\]
\[ E_n \approx E_n^o + E_n^1 \label{7.4.8} \]
\(\lambda\) is purely a bookkeeping device: we will set it equal to 1 when we are through! It’s just there to keep track of the orders of magnitudes of the various terms.
However, let's consider the general case for now. Adding the full expansions for the eigenstate (Equation \(\ref{7.4.5}\)) and energies (Equation \(\ref{7.4.6}\)) into the Schrödinger equation for the perturbation Equation \(\ref{7.4.2}\) in
\[ ( H^o + \lambda H^1) | n \rangle = E_n| n \rangle \label{7.4.9}\]
we have
\[ (H^o + \lambda H^1) \left( \sum _ {i=0}^m \lambda ^i| n^i \rangle \right) = \left( \sum_{i=0}^m \lambda^i E_n^i \right) \left( \sum _ {i=0}^m \lambda ^i| n^i \rangle \right) \label{7.4.10}\]
We’re now ready to match the two sides term by term in powers of \(\lambda\). Note that the zeroth-order term, of course, just gives back the unperturbed Schrödinger Equation (Equation \(\ref{7.4.1}\)).
Let's look at Equation \(\ref{7.4.10}\) with the first few two terms of each expansion:
\[ (H^o + \lambda H^1) \left( | n ^o \rangle + \lambda | n^1 \rangle \right) = \left( E _n^0 + \lambda E_n^1 \right) \left( | n ^o \rangle + \lambda | n^1 \rangle \right) \label{7.4.11}\]
\[ H^o | n ^o \rangle + \lambda H^1 | n ^o \rangle + \lambda H^o | n^1 \rangle + \lambda^2 H^1| n^1 \rangle= E _n^0 | n ^o \rangle + \lambda E_n^1 | n ^o \rangle + \lambda E _n^0 | n ^1 \rangle + \lambda^2 E_n^1 | n^1 \rangle \label{7.4.11A}\]
Collecting terms in order of \(\lambda\)
\[ \underset{\text{zero order}}{H^o | n ^o \rangle} + \color{red} \underset{\text{1st order}}{\lambda ( H^1 | n ^o \rangle + H^o | n^1 \rangle )} + \color{blue} \underset{\text{2nd order}} {\lambda^2 H^1| n^1 \rangle} =\color{black}\underset{\text{zero order}}{E _n^0 | n ^o \rangle} + \color{red} \underset{\text{1st order}}{ \lambda (E_n^1 | n ^o \rangle + E _n^0 | n ^1 \rangle )} +\color{blue}\underset{\text{2nd order}}{\lambda^2 E_n^1 | n^1 \rangle} \label{7.4.12}\]
If we expanded Equation \(\ref{7.4.10}\) further we could express the energies and wavefunctions in higher order components.
Zero-Order Terms (\(\lambda=0\))
The zero order terms in the expansion of Equation \(\ref{7.4.10}\) results in just the Schrödinger Equation for the unperturbed system
\[ H^o | n^o \rangle = E_n^o | n^o \rangle \label{Zero}\]
First-Order Terms (\(\lambda=1\))
The summations in Equations \(\ref{7.4.5}\), \(\ref{7.4.6}\), and \(\ref{7.4.10}\) can be truncated at any order of \(\lambda\). For example, the first order perturbation theory has the truncation at \(\lambda=1\).
First order perturbation of Energy
Matching the terms that linear in \(\lambda\) (red terms in Equation \(\ref{7.4.12}\)) and setting \(\lambda=1\) on both sides of Equation \(\ref{7.4.12}\):
\[ H^o | n^1 \rangle + H^1 | n^o \rangle = E_n^o | n^1 \rangle + E_n^1 | n^o \rangle \label{7.4.13}\]
Equation \(\ref{7.4.13}\) is the key to finding the first-order change in energy \(E_n^1\). Taking the inner product of both sides with \(\langle n^o | \):
\[ \langle n^o | H^o | n^1 \rangle + \langle n^o | H^1 | n^o \rangle = \langle n^o | E_n^o| n^1 \rangle + \langle n^o | E_n^1 | n^o \rangle \label{7.4.14}\]
since operating the zero-order Hamiltonian on the bra wavefunction (this is just the Schrödinger equation (Equation \(\ref{Zero}\)) is
\[ \langle n^o | H^o = \langle n^o | E_n^o \label{7.4.15}\]
and via the orthonormality of the unperturbed \(| n^o \rangle\) wavefunctions both
\[ \langle n^o | n^o \rangle = 1 \label{7.4.16}\]
and Equation \(\ref{7.4.14}\) can be simplified
\[ \cancel{E_n^o \langle n^o | n^1 \rangle} + \langle n^o | H^1 | n^o \rangle = \cancel{ E_n^o \langle n^o | n^1 \rangle} + E_n^1 \cancelto{1}{\langle n^o | n^o} \rangle \label{7.4.14new}\]
since the unperturbed set of eigenstates are orthogonal and we can cancel the other term on each side of the equation, we find that
\[ \color{red} E_n^1 = \langle n^o | H^1 | n^o \rangle \label{7.4.17}\]
The first-order change in the energy of a state resulting from adding a perturbing term \(H^1\) to the Hamiltonian is just the expectation value of \(H^1\) in the unperturbed wavefunctions.
That is, within the first order limit, the energies are given by
\[ \color{red} \underbrace{E_n \approx E_n^o + E_n^1 = E_n^o + \langle n^o | H^1 | n^o \rangle}_{\text{First Order Perturbation Theory}}\]
First order perturbation of Eigenstates
The general expression for the first-order change in the wavefunction is found by taking the inner product of the first-order expansion (Equation \(\ref{7.4.13}\)) with the bra \( \langle m^o |\) with \(m \neq n\),
\[ \langle m^o | H^o | n^1 \rangle + \langle m^o |H^1 | n^o \rangle = \langle m^o | E_n^o | n^1 \rangle + \langle m^o |E_n^1 | n^o \rangle \label{7.4.18}\]
Last term on right side of Equation \(\ref{7.4.18}\)
The last integral on the right hand side of Equation \(\ref{7.4.18}\) is zero, since \(m \neq n\) so
\[ \langle m^o |E_n^1 | n^o \rangle = E_n^1 \langle m^o | n^o \rangle \label{7.4.19}\]
and
\[\langle m^o | n^o \rangle = 0 \label{7.4.20}\]
First term on right side of Equation \(\ref{7.4.18}\)
The first integral is more complicated, since \(\langle m^o |\) are the eigenstates of \(H^0\), we can apply the unperturbed Hamiltonian \(H^o\) to the left (bra)
\[ \langle m^o | H^o | n^1 \rangle = E_m^o \langle m^o | n^1 \rangle \label{7.4.21}\]
which is just this eigenvalue equation
\[ \langle m^o | H^o = \langle m^o | E_m^o \label{7.4.22}\]
so Equation \ref{7.4.18} can be simplified
\[\begin{aligned} \langle m^o | H^o | n^1 \rangle + \langle m^o |H^1 | n^o \rangle &= \langle m^o | E_n^o | n^1 \rangle + \langle m^o |E_n^1 | n^o \rangle \\ E_m^o \langle m^o | n^1 \rangle + \langle m^o |H^1 | n^o \rangle &= E_n^o \langle m^o | n^1 \rangle + 0 \end{aligned}\]
which can be simplified to
\[ \langle m^o |H^1 | n^o \rangle = (E_n^o - E_m^o) \langle m^o | n^1 \rangle\]
or
\[ \langle m^o | n^1 \rangle = \dfrac{\langle m^o | H^1 | n^o \rangle}{ E_n^o - E_m^o} \label{7.4.23}\]
Since \(\{\langle m^o | \}\) is a complete basis set, we can expand \(| n^1 \rangle\) in this basis
\[ | n^1 \rangle = \sum _{m \neq n} c_{mn} |m^o \rangle \label{7.4.24AA}\]
where \(c_{mn}\) are the expansion coefficients. Hence, the energy of the perturbed wavefunction can be written at
\[ | n \rangle \approx | n^o \rangle + \sum _{m \neq n} c_{mn} |m^o \rangle \label{7.4.24B}\]
Note that the \(c_{mn}\) coefficients can are \(\langle m^o | n^1 \rangle\) and from Equation \ref{7.4.23} can be written as
\[ c_{mn} = \dfrac{ \langle m^o | H^1| n^o \rangle }{E_n^o - E_m^o} \label{7.4.24C}\]
The wavefunction corrected to first order is:
\[ \color{red} \underbrace{| n \rangle \approx | n^o \rangle + | n^1 \rangle = | n^o \rangle + \sum _{m \neq n} \dfrac{|m^o \rangle \langle m^o | H^1| n^o \rangle }{E_n^o - E_m^o}}_{\text{First Order Perturbation Theory}} \label{7.4.24}\]
The sum in Equation \(\ref{7.4.24}\) is an expansion of the unknown wavefunction correction as a linear combination of known unperturbed wavefunctions with coefficients \(c_{mn}\). Since is justified since the set of original zero-order wavefunctions forms a complete basis set that can describe any function.
The first-order correction to the unperturbed wavefunction is in general an infinite sum of off diagonal matrix elements of \(H^1\).
- However, the denominator argues that terms in this sum will be weighted by states that are of comparable energy. That means in principle, these sum can be truncated easily based off of some criterion.
- Another point to consider is that many of these matrix elements will equal zero depending on the symmetry of the \(\{| n^o \rangle \}\) basis and \(H^1\) (e.g., some \(\langle m^o | H^1| n^o \rangle\) integrals in Equation \(7.4.24\) could be zero due to the integrand having an odd symmetry).
Second Order Terms (\(\lambda=2\))
There are higher energy terms in the expansion of Equation \(\ref{7.4.5}\) (e.g., the blue terms in Equation \(\ref{7.4.12}\)), but are not discussed further here other than noting the whole perturbation process is an infinite series of corrections that ideally converge to the correct answer. It is the truncating this series as a finite level that is the approximation.
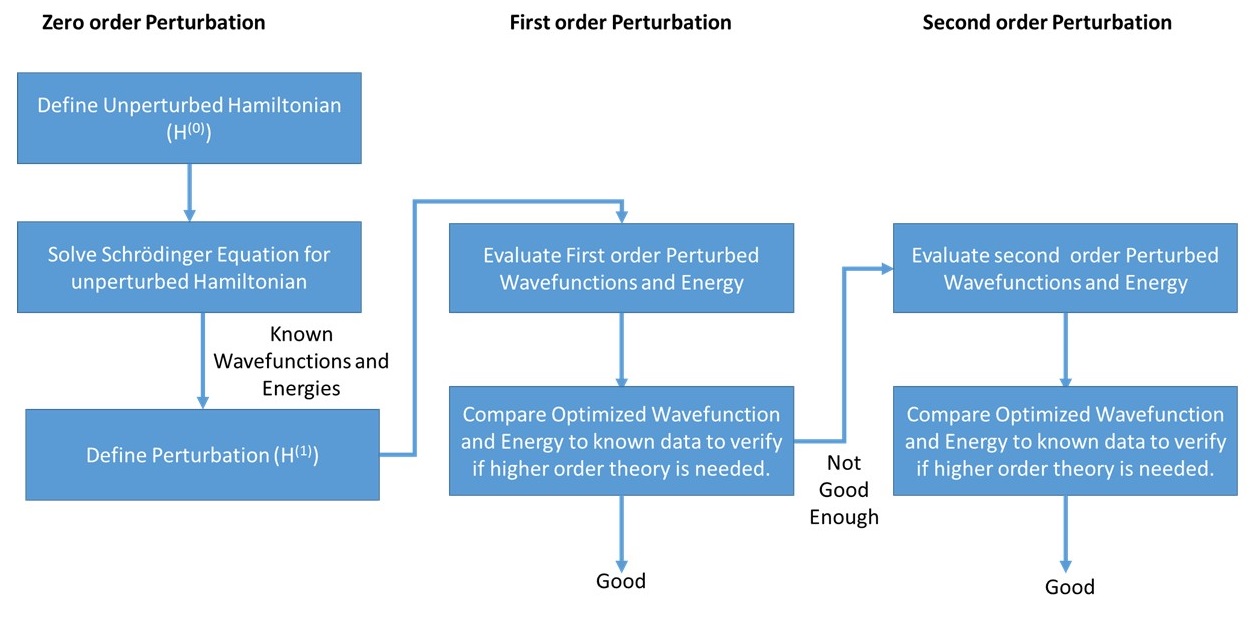
The general approach to perturbation theory applications is giving in the flowchart below. Compare to the flowcharts above for variational method approximations.
Estimate the energy and wavefunction of the ground-state associated with the Hamiltonian using perturbation theory
\[ \hat{H} = \dfrac{-\hbar^2}{2m} \dfrac{d^2}{dx^2} + \dfrac{1}{2} kx^2 + a x^3 \nonumber\]
- Solution (Energy)
-
The first steps in flowchart for applying perturbation theory is to separate the Hamiltonian of the difficult (or unsolvable) problem into a solvable one with a perturbation. For this case, we can rewrite the Hamiltonian as
\[ \hat{H}^{o} + \hat{H}^{1} \nonumber\]
where \(\hat{H}^{o}\) is the Hamitonian for the standard Harmonic Oscillator with known eigenstates and eigenenergies
\[ \hat{H}^{(0)}= \dfrac{-\hbar^2}{2m} \dfrac{d^2}{dx^2} + \dfrac{1}{2} kx^2 \nonumber\]
and \(\hat{H}^{1}\) is the perturbation
\[\hat{H}^{1} = a x^3 \nonumber\]
The first order perturbation is given by Equation \(\ref{7.4.17}\), which for this problem is
\[E_n^1 = \langle n^o | a x^3 | n^o \rangle \nonumber\]
Notice that the integrand has an odd symmetry (i.e., \(f(x)=-f(-x)\)) with the perturbation Hamiltonian being odd and the ground state harmonic oscillator wavefunctions being even. So
\[E_n^1=0 \nonumber\]
In this problem the perturbation to the Hamiltonian is in the potential term. That's good because we don't need to take any derivatives.
\[\hat{H}=-\dfrac{(\hbar)^2}{2m}\dfrac{d}{dx^2}+\dfrac{1}{2}kx^2 + ax^3 \label{1}\]
\[ \begin{align*} \hat{H}^1 &= ax^3 \label{2} \\[4pt] &= \langle \psi_0|\hat{H}^1|\psi_0\rangle \label{3} \\[4pt] &= \langle \psi_0|ax^3|\psi_0\rangle \label{4} \end{align*}\]
Looking at the graph of the Harmonic Oscillator wavefunctions we see that \(\psi_0\) is even.
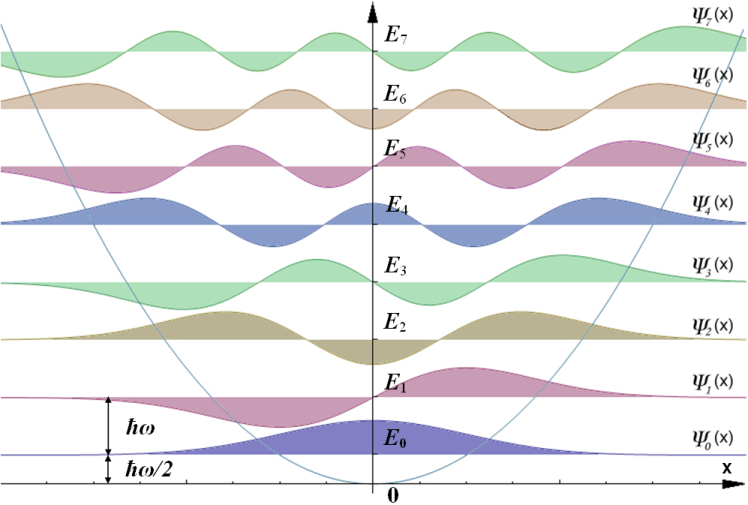
Figure: (CC BY-SA; AllenMcC.from Wikipedia.)
\[\begin{align} E^1 &= \langle \psi_0|ax^3|\psi_0\rangle \\[4pt] &= \langle \text{even}|\text{odd}|\text{even}\rangle \\[4pt] &= \langle odd\rangle = 0 \label{5} \end{align}\]
This means to first order perturbation theory, this cubic terms does not alter the ground state energy. However, this is not the case if second-order perturbation theory were used, which is more accurate (not shown).
\[E_n \approx E_n^o + E_n^1 = E_n^o = \dfrac{1}{2} \hbar \omega\]
This may not be a good approximation, since we expect some change to occur. We may need to expand to second order in energy to see it. Or switch to variational method approach.
- Solution (Wavefunction)
-
Calculating the first order perturbation to the wavefunctions (Equation \(\ref{7.4.24}\)) is more difficult than energy since multiple integrals must be evaluated (an infinite number if symmetry arguments are not applicable). The harmonic oscillator wavefunctions are often written in terms of \(Q\), the unscaled displacement coordinate:
\[ | \Psi _v (x) \rangle = N_v'' H_v (\sqrt{\alpha} Q) e^{-\alpha Q^2/ 2} \nonumber \]
with \(\alpha\)
\[ \alpha = \sqrt{\dfrac{k \mu}{\hbar ^2}} \nonumber\]
and
\[ N_v'' = \sqrt {\dfrac {1}{2^v v!}} \left(\dfrac{\alpha}{\pi}\right)^{1/4} \nonumber\]
Let's consider only the first six wavefunctions that use these Hermite polynomials \(H_v (x)\):
- \(H_0 = 1\)
- \(H_1 = 2x\)
- \(H_2 = -2 + 4x^2\)
- \(H_3 = -12x + 8x^3\)
- \(H_4 = 12 - 48x^2 +16x^4\)
- \(H_5 = 120x - 160x^3 + 32x^5\)
\[| 0^1 \rangle = \dfrac{ \langle 1^o | H^1| 0^o \rangle }{E_0^o - E_1^o} |1^o \rangle + \dfrac{ \langle 2^o | H^1| 0^o \rangle }{E_0^o - E_2^o} |2^o \rangle + \dfrac{ \langle 3^o | H^1| 0^o \rangle }{E_0^o - E_3^o} |3^o \rangle + \dfrac{ \langle 4^o | H^1| 0^o \rangle }{E_0^o - E_4^o} |4^o \rangle + \dfrac{ \langle 5^o | H^1| 0^o \rangle }{E_0^o - E_5^o} |5^o \rangle \nonumber\]
We can use symmetry of the perturbation and unperturbed wavefunctions to solve the integrals above. We know that the unperturbed wavefucntions \(\{|n^{0}\} \rangle\) alternate between even (when \(v\) is even) and odd (when \(v\) is odd). Since the perturbation is an odd function, only when \(m= 2k+1\) with \(k=1,2,3\) would these integrals be non-zero (i.e., for \(m=1,3,5, ...\)).
So of the original five unperturbed wavefunction, only \(|m=2\rangle\) and \(m=4 \rangle\) mix to make the first-order perturbed wavefunction so
\[| 0^1 \rangle = \dfrac{ \langle 1^o | H^1| 0^o \rangle }{E_0^o - E_1^o} |1^o \rangle + \dfrac{ \langle 3^o | H^1| 0^o \rangle }{E_0^o - E_3^o} |3^o \rangle + \dfrac{ \langle 5^o | H^1| 0^o \rangle }{E_0^o - E_5^o} |5^o \rangle \nonumber\]
At this stage, the integrals have to be manually calculated using the defined wavefuctions above, which is left as an exercise. Notice that each unperturbed wavefunction that can "mix" to generate the perturbed wavefunction will have a reciprocally decreasing contribution (w.r.t. energy) due to the growing denominator.
The first order perturbation to the wavefunction (Equation \(\ref{7.4.24}\))
\[ | 0^1 \rangle = \sum _{m \neq 0} \dfrac{|m^o \rangle \langle m^o | H^1| 0^o \rangle }{E_0^o - E_m^o}\]
given these truncated wavefunctions (we should technically use the infinite sum) and that we are considering only the ground state with \(n=0\).
Estimate the energy and wavefunction of the ground-state associated with the Hamiltonian using perturbation theory
\[\hat{H}=-\dfrac{\hbar^2}{2m}\dfrac{d}{dx^2}+\dfrac{1}{2}kx^2 + ax^3 +ax^4 \nonumber\]
- Solution
-
We recognize that this is a perturbation of the harmonic oscillator system and identify the perturbation to the respective HO Hamiltonian.
\[\hat{H}^1=ax^3 + ax^4 \nonumber\]
Now we just have to use Equation \ref{7.4.17} for the first order energy. So we only have to use the lowest energy eigenstate \(| \psi_0 \rangle\):
\[ \begin{align*} E^1 &= \langle \psi_0|\hat{H}^1|\psi_0\rangle \label{8} \\[4pt] &= \langle \psi_0|ax^3 + ax^4|\psi_0\rangle \\[4pt] &= \cancelto{0}{\langle \psi_0|ax^3|\psi_0\rangle} + \langle \psi_0|ax^4|\psi_0\rangle \label{9} \\[4pt] &= \langle \psi_0|ax^4|\psi_0\rangle \\[4pt] &= \int_{-\infty}^{\infty}\left(\dfrac{\alpha}{\pi}\right)^{1/4}e^{-\alpha x^2 / 2} \times ax^4 \times \left(\dfrac{\alpha}{\pi}\right)^{1/4}e^{-\alpha x^2 / 2} dx \label{11} \\[4pt] &= a \left(\dfrac{\alpha}{\pi}\right)^{1/2} \int_{-\infty}^{\infty} x^4 e^{-\alpha x^2} dx \label{12} \\[4pt] &= 2a \left(\dfrac{\alpha}{\pi}\right)^{1/2} \int_{0}^{\infty} x^4 e^{-\alpha x^2} dx \label{13} \\[4pt] &= 2a \left(\dfrac{\alpha}{\pi}\right)^{1/2} \dfrac{3}{8\alpha^2} \left(\dfrac{\pi}{\alpha}\right)^{1/2} \label{14} \\[4pt] &= \dfrac{3a}{4\alpha^2} \label{15} \end{align*}\]
\[E_n \approx E_n^o + E_n^1 = \dfrac{1}{2} \hbar \omega + \dfrac{3a}{4\alpha^2} \nonumber\]
where \( \alpha = \dfrac{m \omega}{\hbar}\) so
\[E_n \approx \dfrac{1}{2} \hbar \omega + \dfrac{3a \hbar^2 }{4 m^2 \omega^2 } \nonumber\]
Does this make sense for the limit when \(a\) goes to zero (turning off perturbation)?

